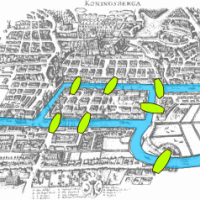
The bridges of Königsberg
This article is part of Five of Euler's best. Click here to read the other four problems featured in this series, which is based on a talk given by the mathematician Günter M. Ziegler at the European Congress of Mathematics 2016.
We'll start with a favourite problems of ours, which we have often visited on Plus (we've even made a movie of it). In the eighteenth century citizens of the Prussian city of Königsberg (now Kaliningrad) had set themselves a puzzle. Königsberg was divided by a river, called the Pregel, which contained two islands with seven bridges linking the various land masses. The puzzle was to find a walk through the city that crossed every bridge exactly once.
Can you find a path that crosses every bridge once and only once? Image: Bogdan Giuşcă.
Euler realised that this type of problem required a new way of thinking. In a letter he wrote to the Italian mathematician and astronomer Giovanni Jacopo Marioni Euler said,
This question is so banal, but seemed to me worthy of attention in that geometry, nor algebra, nor even the art of counting was sufficient to solve it. In view of this, it occurred to me to wonder whether it belonged to the geometry of position which Leibniz had once so much longed for. And so, after some deliberation, I obtained a simple, yet completely established, rule with whose help one can immediately decide for all examples of this kind, with any number of bridges in any arrangement, whether such a round trip is possible, or not....
By geometry of position Euler meant a geometry that isn't concerned with precise measurements of lengths, angles or areas. It's what's today called topology. In the Königsberg problem the exact lay-out of the city doesn't matter. The only thing that is important is how things are connected. Bearing this in mind, you can turn the messy map of the town into a neat network (also called a graph), with dots representing land masses and links between them the bridges.

Transforming the problem. Image: Bogdan Giuşcă.
Euler made a crucial observation: if a path through this network is going to cross every link exactly once, then each node within the path must have an even number of links attached to it. That's because whenever you enter the node by one link, you need to leave it by another, so the node needs two links if you visit it once, four if you visit it twice, and so on. The only nodes that can have an odd number of links attached to them are the nodes where the walk starts and ends (if they are distinct).
This immediately tells us that the path we are looking for doesn't exist in the Königsberg problem. All nodes have an odd number of links attached to them. The beauty of this argument, as Euler suggested in his letter, is that it works for any network, no matter how large or complex. A path that crosses every link exactly once only exists if all, or all but two, nodes have an even number of links attached to them. The converse is also true (though Euler didn't deliver a rigorous proof for this): if all, or all but two, nodes have an even number of links attached to them, then a path that crosses every link exactly once exists.
Euler's thoughts about the Königsberg problem marked the beginning of an area of maths called graph theory, which you might also call network theory. And since we're surrounded by networks, be they social network, transport networks, or the internet, network theory plays an important part in modern mathematics (see here for articles about networks).
If you know Latin, you can read Euler's original paper on the bridges of Königsberg on the Euler archive.
About this article
This article is part of Five of Euler's best. Click here to read the other four problems featured in this series, which is based on a talk given by the mathematician Günter M. Ziegler at the European Congress of Mathematics 2016.
Günter M. Ziegler is professor of Mathematics at Freie Universität Berlin, where he also directs the Mathematics Media Office of the German Mathematical Society DMV. His books include Proofs from THE BOOK (with Martin Aigner) and Do I count? Stories from Mathematics..
Marianne Freiberger is Editor of Plus. She really enjoyed Ziegler's talk about Euler at the European Congress of Mathematics in Berlin in July 2016, on which this article is based.