
Maths in a minute: The Navier-Stokes equations
Turbulence is dramatic, beautiful and potentially dangerous. It happens in liquids, think of breaking waves and raging rivers, as well as gases, for example air streaming around a car or plane. By its very nature, turbulence is incredibly hard to describe. If you measure the speed and direction of water flowing in a turbulent flow you can get very different answers at points that are very close together.

Turbulent water: the Iguassu Falls, border of Brazil and Argentina. Photo: Peter Markowich (see the Plus article Universal pictures).
Despite this complexity, scientists believe that fluid flow is described to a reasonable level of accuracy by the Navier-Stokes equations. When trying to describe the motion of a liquid or gas, what you're after are the velocity $v(x,y,z,t)$ and the pressure $P(x,y,z,t)$ of the liquid at point $(x,y,z)$ in space and at time $t$. The Navier-Stokes equations, named after the physicists Claude-Louis Navier and George Gabriel Stokes, are a set of coupled partial differential equations that relate changes in velocity, changes in pressure and the viscosity of the liquid. To find the functions $v$ and $P$, you have to solve these equations.
But that's no easy feat. Exact solutions to the equations — solutions that can be written down as mathematical formulae — exist only for simplified problems that are of little or no physical interest. For most practical purposes, approximate solutions are found through computer simulations — essentially through educated guess-work — that require immense computing power.
No one knows if exact mathematical solutions even exist for the most general form of the equations. And if they do exist, we still don't know if they involve oddities, such as discontinuities or infinities, that don't square with our intuition of how a liquid should behave. The answer to this question can win you a million dollars from the Clay Mathematics Institute.
To find out more about the Navier-Stokes equations and their many applications — from designing aerodynamically stable footballs to predicting the weather — see these Plus articles.
Here are the equations in their full glory:
The Navier-Stokes equations
At a point (x,y,z) in space, the velocity v(x,y,z) has three components (u,v,w), one for each co-ordinate. The pressure of the liquid is P(x,y,z). Take a deep breath. Here are the equations: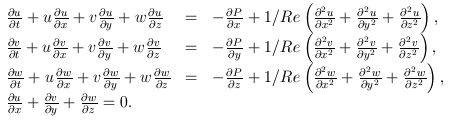
The parameter Re in the equations is called the Reynolds number and measures the viscosity of the liquid.
This article now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
math.nights
Arabic: https://goo.gl/BRe0bP