
| There was an Old Man with a beard, Who said, "It is just as I feared! - Two Owls and a Hen, Four Larks and a Wren, Have all built their nests in my beard!" [Edward Lear] |
Making its first appearance a little over a century ago, the lure of the limerick is such that it has grown to become one of the world's most popular verse forms. There is something strangely appealing and intuitively "natural" about its slightly skewed symmetry.
At about the same time - in fact precisely 100 years ago in 1899 - the music of ragtime was let loose on the world with the publication of Scott Joplin's Maple Leaf Rag, a seminal blend of Western art music traditions combined with African and Latin syncopations. It deserves to be be highlighted as one of the most significant events in the history of music - a trailblazer to the explosive development of contemporary popular music, which is almost certainly one of the most widely-shared cultural experiences on the planet.
There are interesting symmetries shared by the limerick and ragtime, which can be observed and heard in their family groups of stressed and unstressed syllables, or beats, and which lie at the heart of what gives these forms their characteristic structure or "feel". They possess self-similar qualities which are related to fractal models used by contemporary scientists, and can provide a keen insight into some quite profound inter-relationships between the arts and sciences.
We will come back to Ragtime later, but let us first look at the underlying stress patterns in the metre of the limerick by writing it out using "di" for an unstressed syllable and "dum" for a stressed one like this:
di dum di di dum di di dum
di dum di di dum di di dum
di dum di di dum
di dum di di dum
di dum di di dum di di dum
If we count up the different types of syllable, we discover that out of a total of 34 syllables, 21 are unstressed (the di's) and 13 are stressed (the dum's). There are 8 syllables in the longer lines and 5 in the shorter ones. Out of the total of 5 lines, 3 are long ones containing 3 metrical feet (i.e. 3 stressed dum's), and 2 are shorter ones containing 2 metrical feet. Anyone familiar with elementary mathematics will recognise these numbers as belonging to the well known Fibonacci series: 1, 1, 2, 3, 5, 8, 13, 21, 34 ... where each successive number is the sum of the two preceding numbers (see The Life and Numbers of Fibonacci) in Issue 3 of Plus. This series is, of course, well-known for matching growth patterns in nature - in daisies, pineapples, sunflowers, pine cones, sea shells, trees, corals - there's scarcely a branch of science where Fibonacci's numbers do not show up in some form or another. But is the appearance of these numbers in relation to the limerick merely coincidence, or are they significant?
The point is, that nested hierarchies of Fibonacci relationships pervade the whole structure of the limerick, and in particular, demonstrate one of the most powerful tools used in mathematical modelling - the concept of recursion and its inevitable outcome, self-similarity.
Recursion can be loosely explained as "defining something in terms of itself". A common example is the picture of a man holding a picture, which is a picture of himself holding a picture, which is a picture of himself holding a picture ... and so on, until the image gets too small to see any more detail. The situation gets more interesting if we imagine a picture of a man holding two pictures, one in each arm, each of which is a copy of the original picture - and the two pictures inside each picture themselves contain two pictures ... and so on. This is a more potent form of recursion where the patterns rapidly become more complex as the process continues. At the top level there is one picture, inside it at the next level down there are 2 pictures, counting the pictures nested inside those for the next level down gives a total of 4, after one more level there are 8 ... and so on.
This can be easier to visualise if we think of the levels as stacking upwards, and relate it to the way branches split and grow to make trees. We can make a formal definition of an ideal branch like this: a branch is defined as a bough with two smaller branches at the end.
Then each of the smaller branches again has two smaller branches on the end, they in turn split into smaller branches, and so on. It is a relatively straightforward matter to write a computer graphics program based on this simple definition - a binary splitting algorithm - which will automatically continue this recursive process to whatever level of detail and complexity is required, to produce a whole forest of simulated trees.
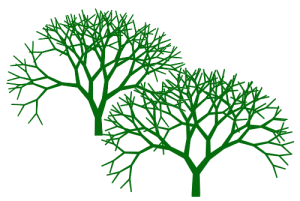
Figure 1: Simulated trees with binary splitting.
To understand the great power and rich potential of recursion requires something of a leap of the imagination, but it is not hard to grasp, and the way the Fibonacci pattern is derived provides an even more subtle example. Fibonacci is actually the nickname given to a twelfth century mathematician, Leonardo of Pisa, who published a seemingly innocuous but now celebrated recreational mathematical problem about breeding rabbits.
Fibonacci's Problem
A pair of rabbits mature, breed and produce a pair of baby rabbits. Next season they produce another pair to join their siblings - 3 pairs altogether. Next season they breed again, and so do the older siblings, now old enough to breed themselves, whilst the younger siblings are not yet old enough to breed - 5 pairs altogether - and so on. The question is, if parent rabbits can breed every season, whilst infant rabbits need a season to mature and become parents, (and assuming no rabbits die!) how many pairs will there be after a given number of seasons?
In recent years, similar scenarios have been used to model the growth of cells in biological organisms. The biologist Lindenmayer has given his name to what are known as L-systems, used to model the growth of plants or expanding cell populations. These use re-write rules, where an object or symbol to the left of an arrow is replaced by the object or symbols to the right. So using an L-system type notation, Fibonacci's first rule tells us that in a breeding season a pair of adults will become that same pair again plus a pair of offspring:
Rule (1): adult → adult + offspringAt the same time, last season's offspring will become adults:
Rule (2): offspring → adult
These rules can be applied not only to pairs of rabbits, but also to cells, or to adult branches and offspring branches when modelling the growth of a tree - indeed any situation where growth in seasons of time is being modelled.
To help follow what happens as Fibonacci's L-system type rules are applied over a number of generational seasons, we can abbreviate adult to A and offspring to O, giving us the rules:
Rule (1): A → A + O
Rule (2): O → A
Beginning with A, after one generation we have A + O. After two generations the A has become A + O again, and the O has now become A, so our population of three could be written as (A + O) + A. The third generation could be written as ((A + O) + A ) + (A + O). It gets a bit clumsy showing the generational relationships with brackets - a tree diagram gives a clearer picture as the generations continue:
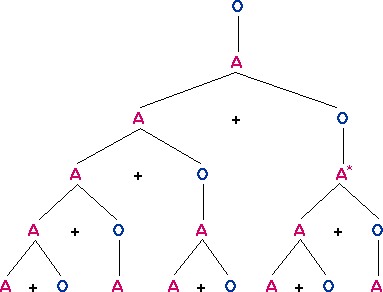
Figure 2: Generation tree for a Fibonacci-type L-system.
When writing Rule (1), we wrote down the adult first, followed by the offspring, but there is no reason why we could not have put the offspring first, like this
Alternative Rule (1): A → O + A
This means that at key points in the generational tree, we can reverse the order. When rabbits breed or plants grow in three dimensional space the precise orientation of their various branches and offshoots may move around, but the Fibonacci-type generative relationships are still preserved. If at the starred position in Figure 2 above, the order of the next generation is reversed, we end up with this pattern:
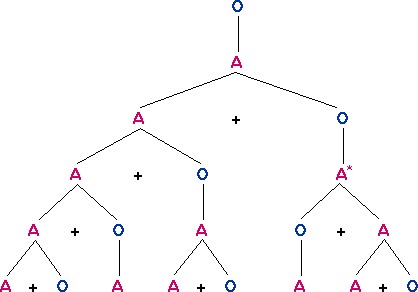
Figure 3: Variant generation tree for a Fibonacci-type L-system.
You may by now have spotted that the pattern of A's and O's at the bottom is identical to a line of the limerick, where A's represent unstressed syllables (di's), and O's stressed syllables (dum's). The pattern may be continued through further generations to produce the precise metric form of the limerick - see Figure 4. This pattern contains all sorts of exciting symmetries and nested patterns which are self-similar to shapes higher up the generational tree - all of which arise inevitably from the repeated application of the simple generative rules. In Figure 5 a slightly different parsing tree is turned upside down and shaded to highlight the branching relationships, which makes the biological parallel more obvious.
The fact that such a remarkable pattern underpins the structure of the limerick suggests that this helps to account for its "naturally" appealing qualities - it is almost as if the brain is hard-wired to match or harmonise with these patterns in nature, and that the mind's aesthetic responses will naturally be pulled towards these attractive patterns.
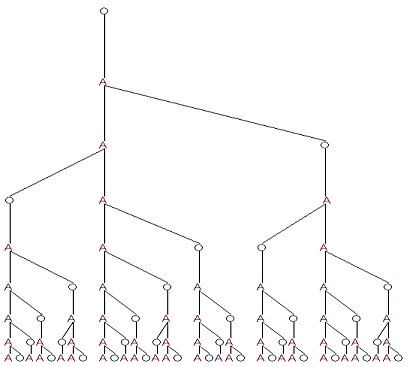
Figure 4: Fibonacci-type L-system derivation tree for the limerick metre.
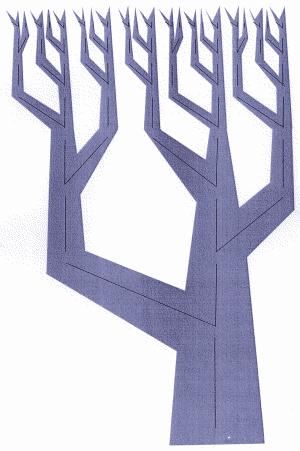
Figure 5: An alternative parsing of the same pattern inverted and shaded to resemble a tree.
Perceiving the underlying metre of the limerick is not just a simple linear experience. The generational grammar and symmetrical relationships which inhabit the structure effectively map out a sort of hierarchy of simultaneity. As the first few words are revealed - by listening to the poem being read out loud, or else by "virtually" hearing the patterns when silently reading the text - the self-similar nature of the pattern provides the mind with enough clues to intuitively predict and anticipate what is coming, and feel a surge of satisfaction as the structure inevitably unfolds - reinforced by the rhyming patterns at the end of the lines.
Of course, in the real world, cells - and rabbits - will die, plant stems and branches will be stunted and distorted by interfering natural forces such as the weather and hungry animals, and so perfect realizations of the model may not be the norm. It can nevertheless exist as a cognitive point of reference, helping the mind to categorise and engage with the world.
A similar point applies to limericks - they do not all have the "perfect" Fibonacci symmetry we have just described. In particular, they may often have an extra weak syllable at the end of lines. For instance:
There was a young lady from Ealing
Whose kisses were warm and appealing.
If someone complained
Her passion was feigned,
She'd kiss them again with more feeling.
In many limericks extra weak syllables may be squeezed in almost anywhere, but we still recognise or relate it to a familiar underlying metrical pattern. We may even feel rather cheated if the poet has taken too many liberties, and value the ingenuity and elegance of the purest forms - which are easier to remember. In each case the underlying pattern of metrical feet is still intact, and the generative relationships are preserved. Those extra syllables could be thought of as new generational shoots beginning to bud.
Picking out different stress patterns found by reading across an earlier generation level in the derivation trees of Figures 4 and 5, produces what could be termed "proto-limericks" which have similarly satisfying symmetries in their metrical rhythm. This pattern could be considered the prototype for a new verse form known as a "Merrick" perhaps:
di dum di di dumwhich might give us something like this:
di dum di di dum
di dum di
di dum di
di dum di di dum
He skewered the slug
And gave it a tug.
"This cabbage,"
said Babbage,
"Is hard to debug."
Whilst this pattern could perhaps be called a "Limer":
di dum di di dum di di dumGiving us verses like this:
di dum di di dum
There was a young farmer from Kentor
Whose beans were all bent.
Whenever she went to Brazil
She always fell ill.
The stress patterns of rhythm and metre which distinguish verse forms are also, of course, intrinsic to the structure and impact of music - this is where Scott Joplin's Maple Leaf Rag fits in. Figure 6 shows the familiar musical motif which comes at the start of the second half of the rag - in the first two bars:

Figure 6: Start of the second half of Scott Joplin's Maple Leaf Rag.
Using the same coding syllables that we used for showing the metrical stresses of the limerick, we can write the rhythm of the upper melodic part, played by the right hand, like this:
di dum di di dumOf the 13 "note events", 8 are unstressed (di's - single notes) and 5 are stressed (dum's - notes with octave doubling), and they break into a Fibonacci-style 5 + (5 + 3) grouping. At the same time the left hand plays a regular 8 note or chordal um-pah um-pah accompaniment. The 13 right-hand and 8 left-hand note-events together produce the satisfying Fibonacci total of 21. The melody here can be parsed for nested relationships in a similar (but not quite identical) way to the limerick pattern.
di dum di di dum
di dum di
Another piece of jazz-inspired music which has an identical metrical pattern to the limerick is the song It ain't necessarily so from George Gershwin's Porgy and Bess(1935). Whereas there is no suggestion that the metrical rhythms of limerick and ragtime were deliberately worked out, but rather that they emerge as an inevitable reflection of nature - with Gershwin there may be an element of deliberate shaping involved. Along with a number of popular American composers from the first half of the twentieth century he was taught by the remarkable engineer and musician Joseph Schillinger. His massive tomes, The Mathematical Basis of the Arts and The Schillinger System of Musical Composition, suggest many different systems for generating rhythm patterns and other forms of musical material which Schillinger explicitly relates to patterns in the physical world. He mentions the Fibonacci sequence as being rather special, but its potential is only hinted at and not developed. Gershwin was diligently supervised by Schillinger during the composition of Porgy and Bess, but a detailed study of the extent of this influence has yet to be completed.
Musicologists have uncovered Fibonacci patterns and related Golden Section proportions in the work of many other composers, particularly figures such as Debussy and Bartok whose work looked to folk and other influences outside of the European mainstream.
For many centuries, European "high" culture - including music and poetry - was dominated by four-square classical forms, safely predictable and ordered. Ideally music was expected to be formed from neat phrases of four or eight bars, which would be combined into 16-bar subjects, with rhythmic notation based on a binary hierarchy which current American terminology of half-notes, quarter-notes, eighth-notes etc. reinforces. In short, it was a "binarist" system - equivalent to the more basic binary tree models described near the beginning of this article. In practice this system essentially formed an ideal point of reference to which only the dullest (but often popular) composers would slavishly adhere. More imaginative minds such as Mozart and Beethoven found stimulating ways of subverting the system - though their contemporaries were often wary of their more radical excesses.
What the limerick and ragtime have in common is the way in which they reconcile traditional "binarist" structure with skewed Fibonacci symmetries. With the limerick, the two shorter third and fourth lines can fill the same time span as each of the longer lines - so giving an underlying feel of four equal lines. This arrangement is common in other popular, semi-serious genres such as Nursery Rhymes. Hickory Dickory Dock, for instance, has the same underlying structure as the limerick. Similarly, the music of Ragtime has a "safe" four-square left-hand anchoring the "dangerous" syncopated meanderings of the right hand melodies.
The syncopated, skewed metres and rhythms of folk and popular music have even in the recent past been considered degenerate and uncultured by more conservative commentators. The very name "Ragtime" suggests something ragged and rough - uncouth and uncomfortable to those reared on "binarist" prejudice - and so it is no surprise that the limerick's favoured subjects usually relate to rather "earthy" matters. But during the Twentieth Century the Fibonacci paradigm has emerged triumphant, and entered the mainstream to form a more subtle and natural structural template, or cultural point of reference, against which our minds can measure their aesthetic response.
We have seen how the structural patterns in music and verse can reflect patterns in the natural world, and that we can use mathematical models to help make that comparison, but might familiar cultural products such as popular verse and music influence the way in which science and mathematics develop? Mathematics is about pattern, about looking for codes as short-hand ways of describing more complicated things, deciding what patterns are significant and what are not - and this often relies on aesthetic judgement to decide which out of various competing alternatives are the most elegant or appealing. Physical scientists find uses for mathematical models, applying them to help understand processes and patterns in the real world. This too requires an intuitive sense of beauty, or some sort of developed "inner harmony" which makes the mind feel good when it knows it has got it right. It seems quite reasonable, then, to suppose that a sense of harmony and proportion will be influenced by familiarity with the arts. Music is the language of "harmony" in its fundamental sense - it has been called "audible mathematics". There are many examples of scientists from Newton to Einstein admitting to its inspirational role in freeing up creative thought. Historically music theory developed in tandem with scientific theory - indeed music was considered to be a branch of science - so it was natural that leading scientific and musical advances were made by the same minds.
The so-called "Mozart Effect" is attracting a lot of interest, particularly in the United States, where experiments have led to the claim that regular listening to Mozart will improve a child's IQ. There is something about such subtle musical structures which seems to act as a benign mental stimulus in all the right places. It is unlikely that such an effect would be limited to Mozart's music alone - but it draws attention to the profound influence which music can have on the mind. Music is the most subtle medium humankind has developed for experiencing and exploring patterns in time, and its significance for science should never be underestimated. Music is not mere entertainment, it is good for the mind as well as the soul. The music of the spheres rings as true as ever.
This is the winning essay in The THES/OUP Science Writing Prize for 1999, and appears with the kind permission of OUP.
©OUP 1999.
About the author

Dr Kevin Jones is Reader in Music at Kingston University in Surrey. He has degrees in Mathematics and Computer Science as well as in Music.
He is particularly interested in exploring the underlying relationships between music, science and culture - in his research, and in his work as writer, composer and teacher.