
This lecture, by Stephen Hawking, was first presented at "The Future of Theoretical Physics and Cosmology: Stephen Hawking 60th Birthday Symposium" at the Centre for Mathematical Sciences, Cambridge, UK, on 11 January 2002. It is reprinted in Plus by permission.
![[IMAGE: ]](/issue18/features/hawking/images/nutshell.jpg)
The universe in a nutshell
I will skip over the first twenty of my sixty years, and pick up the story in October 1962, when I arrived in Cambridge as a graduate student. I had applied to work with Fred Hoyle, the principal defender of the steady state theory, and the most famous British astronomer of the time. I say astronomer, because cosmology was at that time hardly recognised as a legitimate field, yet that was where I wanted to do my research, inspired by having been on a summer course with Hoyle's student, Jayant Narlikar.
However, Hoyle had enough students already, so to my great disappointment I was assigned to Dennis Sciama, of whom I had not heard. But it was probably for the best. Hoyle was away a lot, seldom in the department, and I wouldn't have had much of his attention. Sciama, on the other hand, was usually around, and ready to talk. I didn't agree with many of his ideas, particularly on Mach's Principle, but that stimulated me to develop my own picture.
When I began research, the two areas that seemed exciting were cosmology, and elementary particle physics. Elementary particles was the active, rapidly changing field, that attracted most of the best minds, while cosmology and general relativity were stuck where they had been in the 1930s. Feynman has given an amusing account of attending the conference on general relativity and gravitation, in Warsaw in 1962. In a letter to his wife, he said
"I am not getting anything out of the meeting. I am learning nothing. Because there are no experiments, this field is not an active one, so few of the best men are doing work in it. The result is that there are hosts of dopes here (126) and it is not good for my blood pressure. Remind me not to come to any more gravity conferences!"
Of course, I wasn't aware of all this when I began my research. But I felt that [the research area of] elementary particles, at that time, was too like botany. Quantum Electrodynamics, the theory of light and electrons that governs chemistry and the structure of atoms, had been worked out completely in the 40s and 50s. Attention had now shifted to the weak and strong nuclear forces between particles in the nucleus of an atom, but similar field theories didn't seem to work. Indeed, the Cambridge school, in particular, held that there was no underlying field theory. Instead, everything would be determined by unitarity, that is, probability conservation, and certain characteristic patterns in the scattering.
With hindsight, it now seems amazing that it was thought this approach would work, but I remember the scorn that was poured on the first attempts at unified field theories of the weak nuclear forces. Yet it is these field theories that are remembered, and the analytic S-matrix work is forgotten. I'm very glad I didn't start my research in elementary particles. None of my work from that period would have survived.
Cosmology and gravitation, on the other hand, were neglected fields, that were ripe for development at that time. Unlike elementary particles, there was a well-defined theory, the general theory of relativity, but this was thought to be impossibly difficult. People were so pleased to find any solution of the field equations [that] they didn't ask what physical significance, if any, it had. This was the old school of general relativity that Feynman encountered in Warsaw. But the Warsaw conference also marked the beginning of the renaissance of general relativity, though Feynman could be forgiven for not recognising it at the time.
A new generation entered the field, and new centres of general relativity appeared. Two of these were of particular importance to me. One was in Hamburg under Pascual Jordan. I never visited it, but I admired their elegant papers, which were such a contrast to the previous messy work on general relativity. The other centre was at Kings College, London, under Hermann Bondi, another proponent of the steady state theory, but not ideologically committed to it, like Hoyle.
I hadn't done much mathematics at school, or in the very easy physics course at Oxford, so Sciama suggested I work on astrophysics. But having been cheated out of working with Hoyle, I wasn't going to do something boring like Faraday rotation. I had come to Cambridge to do cosmology, and cosmology I was determined to do. So I read old text books on general relativity, and travelled up to lectures at Kings College, London each week, with three other students of Sciama. I followed the words and equations, but I didn't really get a feel for the subject. Also, I had been diagnosed with motor neurone disease, or ALS, and given to expect I didn't have long enough to finish my PhD.
Then suddenly, towards the end of my second year of research, things picked up. My disease wasn't progressing much, and my work all fell into place, and I began to get somewhere. Sciama was very keen on Mach's principle, the idea that objects owe their inertia to the influence of all the other matter in the universe. He tried to get me to work on this, but I felt his formulations of Mach's Principle were not well-defined.
However, he introduced me to something a bit similar with regard to light, the so-called Wheeler-Feynman electrodynamics. This said that electricity and magnetism were time-symmetric. However, when one switched on a lamp, it was the influence of all the other matter in the universe that caused light waves to travel outward from the lamp, rather than come in from infinity, and end on the lamp. For Wheeler-Feynman electrodynamics to work, it was necessary that all the light travelling out from the lamp should be absorbed by other matter in the universe. This would happen in a steady state universe, in which the density of matter would remain constant, but not in a big bang universe, where the density would go down as the universe expanded.
![[IMAGE:Mr X ]](/issue18/features/hawking/images/mrx.gif)
It was claimed that this was another proof, if proof were needed, that we live in a steady state universe. There was a conference on Wheeler-Feynman electrodynamics, and the arrow of time, in 1963. Feynman was so disgusted by the nonsense that was talked about the arrow of time that he refused to let his name appear in the proceedings. He was referred to as Mr X, but everyone knew who X was.
I found that Hoyle and Narlikar had already worked out Wheeler-Feynman electrodynamics in expanding universes, and had then gone on to formulate a time-symmetric new theory of gravity. Hoyle unveiled the theory at a meeting of the Royal Society in 1964. I was at the lecture, and in the question period, I said that the influence of all the matter in a steady state universe would make his masses infinite. Hoyle asked why I said that, and I replied that I had calculated it. Everyone thought I had done it in my head during the lecture, but in fact, I was sharing an office with Narlikar, and had seen a draft of the paper. Hoyle was furious. He was trying to set up his own institute, and threatening to join the brain drain to America if he didn't get the money. He thought I had been put up to it, to sabotage his plans. However, he got his institute, and later gave me a job, so he didn't harbor a grudge against me.
The big question in cosmology in the early 60's was, did the universe have a beginning? Many scientists were instinctively opposed to the idea, because they felt that a point of creation would be a place where science broke down. One would have to appeal to religion and the hand of God, to determine how the universe would start off. Two alternative scenarios were therefore put forward. One was the steady state theory, in which as the universe expanded, new matter was continually created to keep the density constant on average. The steady state theory was never on a very strong theoretical basis, because it required a negative energy field to create the matter. This would have made it unstable to runaway production of matter and negative energy. But it had the great merit as a scientific theory, of making definite predictions that could be tested by observations.
![[IMAGE: Telescope]](/issue18/features/hawking/images/one-mile-telescope.jpg)
Radio Telescope
By 1963, the steady state theory was already in trouble. Martin Ryle's radio astronomy group at the Cavendish did a survey of faint radio sources. They found the sources were distributed fairly uniformly across the sky. This indicated that they were probably outside our galaxy, because otherwise they would be concentrated along the Milky Way. But the graph of the number of sources against source strength did not agree with the prediction of the steady state theory. There were too many faint sources, indicating that the density of sources was higher in the distant past.
Hoyle and his supporters put forward increasingly contrived explanations of the observations, but the final nail in the coffin of the steady state theory came in 1965 with the discovery of a faint background of microwave radiation. This could not be accounted for in the steady state theory, though Hoyle and Narlikar tried desperately. It was just as well I hadn't been a student of Hoyle, because I would have had to have defended the steady state.
The microwave background indicated that the universe had had a hot dense stage, in the past. But it didn't prove that was the beginning of the universe. One might imagine that the universe had had a previous contracting phase, and that it had bounced from contraction to expansion, at a high, but finite density. This was clearly a fundamental question, and it was just what I needed to complete my PhD thesis.
Gravity pulls matter together, but rotation throws it apart. So my first question was, could rotation cause the universe to bounce? Together with George Ellis, I was able to show that the answer was no, if the universe was spatially homogeneous, that is, if it was the same at each point of space. However, two Russians, Lifshitz and Khalatnikov, had claimed to have proved that a general contraction without exact symmetry would always lead to a bounce, with the density remaining finite. This result was very convenient for Marxist-Leninist dialectical materialism, because it avoided awkward questions about the creation of the universe. It therefore became an article of faith for Soviet scientists.
Lifshitz and Khalatnikov were members of the old school in general relativity. That is, they wrote down a massive system of equations, and tried to guess a solution. But it wasn't clear that the solution they found was the most general one. However, Roger Penrose introduced a new approach, which didn't require solving the field equations explicitly, just certain general properties, such as that energy is positive, and gravity is attractive. Penrose gave a seminar in Kings College, London, in January 1965. I wasn't at the seminar, but I heard about it from Brandon Carter, with whom I shared an office in the then new DAMTP premises in Silver Street.
At first, I couldn't understand what the point was. Penrose had showed that once a dying star had contracted to a certain radius, there would inevitably be a singularity, a point where space and time came to an end. Surely, I thought, we already knew that nothing could prevent a massive cold star collapsing under its own gravity until it reached a singularity of infinite density. But in fact, the equations had been solved only for the collapse of a perfectly spherical star. Of course, a real star won't be exactly spherical. If Lifshitz and Khalatnikov were right, the departures from spherical symmetry would grow as the star collapsed, and would cause different parts of the star to miss each other, and avoid a singularity of infinite density. But Penrose showed they were wrong. Small departures from spherical symmetry will not prevent a singularity.
I realised that similar arguments could be applied to the expansion of the universe. In this case, I could prove there were singularities where space-time had a beginning. So again, Lifshitz and Khalatnikov were wrong. General relativity predicted that the universe should have a beginning, a result that did not pass unnoticed by the Church.
The original singularity theorems of both Penrose and myself required the assumption that the universe had a Cauchy surface, that is, a surface that intersects every time-like curve once, and only once. It was therefore possible that our first singularity theorems just proved that the universe didn't have a Cauchy surface. While interesting, this didn't compare in importance with time having a beginning or end.
I therefore set about proving singularity theorems that didn't require the assumption of a Cauchy surface. In the next five years, Roger Penrose, Bob Geroch, and I developed the theory of causal structure in general relativity. It was a glorious feeling, having a whole field virtually to ourselves. How unlike particle physics, where people were falling over themselves to latch onto the latest idea. They still are. Up to 1970, my main interest was in the big bang singularity of cosmology, rather than the singularities that Penrose had shown would occur in collapsing stars. However, in 1967, Werner Israel produced an important result. He showed that unless the remnant from a collapsing star was exactly spherical, the singularity it contained would be naked, that is, it would be visible to outside observers. This would have meant that the breakdown of general relativity at the singularity of a collapsing star would destroy our ability to predict the future of the rest of the universe.
![[IMAGE: ]](/issue18/features/hawking/images/bumper_sticker.jpg)
At first, most people, including Israel himself, thought that this implied that because real stars aren't spherical, their collapse would give rise to naked singularities, and breakdown of predictability. However, a different interpretation was put forward by Roger Penrose and John Wheeler. It was that there is Cosmic Censorship. This says that Nature is a prude, and hides singularities in black holes, where they can't be seen. I used to have a bumper sticker [saying] "Black Holes are out of sight" on the door of my office in DAMTP. This so irritated the head of department that he engineered my election to the Lucasian professorship, moved me to a better office on the strength of it, and personally tore off the offending notice from the old office.
My work on black holes began with a Eureka moment in 1970, a few days after the birth of my daughter, Lucy. While getting into bed, I realised that I could apply to black holes the causal structure theory I had developed for singularity theorems. In particular, the area of the horizon, the boundary of the black hole, would always increase. When two black holes collide and merge, the area of the final black hole is greater than the sum of the areas of the original holes. This, and other properties that Jim Bardeen, Brandon Carter, and I discovered, suggested that the area was like the entropy of a black hole. This would be a measure of how many states a black hole could have on the inside, for the same appearance on the outside. But the area couldn't actually be the entropy, because as everyone knew, black holes were completely black, and couldn't be in equilibrium with thermal radiation.
![[IMAGE: tshirt]](/issue18/features/hawking/images/t-shirt.jpg)
There was an exciting period culminating in the Les Houches summer school in 1972, in which we solved most of the major problems in black hole theory. This was before there was any observational evidence for black holes, which shows Feynman was wrong when he said an active field has to be experimentally driven. Just as well for M theory. The one problem that was never solved was to prove the Cosmic Censorship hypothesis, though a number of attempts to disprove it failed. It is fundamental to all work on black holes, so I have a strong vested interest in it being true. I therefore have a bet with Kip Thorne and John Preskill. It is difficult for me to win this bet, but quite possible to lose, by finding a counter example with a naked singularity. In fact, I have already lost an earlier version of the bet, by not being careful enough about the wording. They were not amused by the T-shirt I offered in settlement.
We were so successful with the classical general theory of relativity that I was at a bit of a loose end in 1973, after the publication with George Ellis, of The Large Scale Structure of Space-time. My work with Penrose had shown that general relativity broke down at singularities. So the obvious next step would be to combine general relativity, the theory of the very large, with quantum theory, the theory of the very small. I had no background in quantum theory, and the singularity problem seemed too difficult for a frontal assault at that time. So as a warm-up exercise, I considered how particles and fields governed by quantum theory would behave near a black hole.
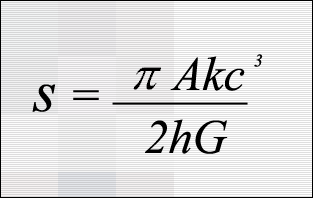
The black hole entropy formula.
In particular, I wondered, can one have atoms in which the nucleus is a tiny primordial black hole, formed in the early universe? To answer this, I studied how quantum fields would scatter off a black hole. I was expecting that part of an incident wave would be absorbed, and the remainder scattered. But to my great surprise, I found there seemed to be emission from the black hole. At first, I thought this must be a mistake in my calculation. But what persuaded me that it was real, was that the emission was exactly what was required to identify the area of the horizon with the entropy of a black hole. I would like this simple formula to be on my tombstone.
Work with Jim Hartle, Gary Gibbons, and Malcolm Perry uncovered the deep reason for this formula. General relativity can be combined with quantum theory in an elegant manner, if one replaces ordinary time by imaginary time. I have tried to explain imaginary time on other occasions, with varying degrees of success. I think it is the name, imaginary, that makes it so confusing. It is easier if you accept the positivist view, that a theory is just a mathematical model. In this case, the mathematical model has a minus sign whenever time appears twice. The Euclidean approach to quantum gravity, based on imaginary time, was pioneered in Cambridge. It met a lot of resistance, but is now generally accepted.
Between 1970 and 1980, I worked mainly on black holes and the Euclidean approach to quantum gravity. But the suggestions that the early universe had gone through a period of inflationary expansion renewed my interest in cosmology. Euclidean methods were the obvious way to describe fluctuations and phase transitions in an inflationary universe. We held a Nuffield workshop in Cambridge in 1982, attended by all the major players in the field. At this meeting, we established most of our present picture of inflation, including the all-important density fluctuations, which give rise to galaxy formation, and so to our existence. This was ten years before fluctuations in the microwave were observed, so again in gravity, theory was ahead of experiment.
The scenario for inflation in 1982 was that the universe began with a big bang singularity. As the universe expanded, it was supposed somehow to get into an inflationary state. I thought this was unsatisfactory, because all equations would break down at a singularity. But unless one knew what came out of the initial singularity, one could not calculate how the universe would develop. Cosmology would not have any predictive power.
After the workshop in Cambridge, I spent the summer at the Institute of Theoretical Physics, Santa Barbara, which had just been set up. We stayed in student houses, and I drove in to the institute in a rented electric wheel chair. I remember my younger son Tim, aged three, watching the Sun set on the mountains, and saying, "It's a big country."
While in Santa Barbara, I talked to Jim Hartle about how to apply the Euclidean approach to cosmology. According to Dewitt and others, the universe should be described by a wave function that obeyed the Wheeler Dewitt equation. But what picked out the particular solution of the equation that represents our universe? According to the Euclidean approach, the wave function of the universe is given by a Feynman sum over a certain class of histories in imaginary time. Because imaginary time behaves like another direction in space, histories in imaginary time can be closed surfaces, like the surface of the Earth, with no beginning or end. Jim and I decided that this was the most natural choice of class, indeed the only natural choice. We had side-stepped the scientific and philosophical difficulty of time beginning, by turning it into a direction in space.
Most people in theoretical physics have been trained in particle physics, rather than general relativity. They have therefore been more interested in calculations of what they observe in particle accelerators, than in questions about the beginning and end of time. The feeling was that if they could find a theory that in principle allowed them to calculate particle scattering to arbitrary accuracy, everything else would somehow follow. In 1985, it was claimed that string theory was this ultimate theory. But in the years that followed, it emerged that the situation was more complicated, and more interesting.
![[IMAGE: ]](/issue18/features/hawking/images/M-theory-Network.jpg)
It seems that there's a network called M theory. All the theories in the M theory network can be regarded as approximations to the same underlying theory, in different limits. None of the theories allow calculation of scattering to arbitrary accuracy, and none can be regarded as the fundamental theory, of which others are reflections. Instead, they should all be regarded as effective theories, valid in different limits. String theorists have long used the term "effective theory" as a pejorative description of general relativity, but string theory is equally an effective theory, valid in the limit that the M theory membrane is rolled into a cylinder of small radius. Saying that string theory is only an effective theory isn't very popular, but it's true.
The dream of a theory that would allow calculation of scattering to arbitrary accuracy led people to reject quantum general relativity and supergravity, on the grounds that they were non-renormalizable. This means that one needs undetermined subtractions at each order, to get finite answers. In fact, it is not surprising that naive perturbation theory breaks down in quantum gravity. One can not regard a black hole as a perturbation of flat space.
I have done some work recently, on making supergravity renormalizable, by adding higher derivative terms to the action. This apparently introduces ghosts, states with negative probability. However, I have found this is an illusion. One can never prepare a system in a state of negative probability. But the presence of ghosts that one can not predict with arbitrary accuracy. If one can accept that, one can live quite happily with ghosts.
![[IMAGE: ]](/issue18/features/hawking/images/orign-of-universe.jpg)
The origin of the universe
This approach to higher derivatives and ghosts allows one to revive the original inflation model, of Starobinskii and other Russians. In this, the inflationary expansion of the universe, is driven by the quantum effects of a large number of matter fields. Based on the no boundary proposal, I picture the origin of the universe, as like the formation of bubbles of steam in boiling water. Quantum fluctuations lead to the spontaneous creation of tiny universes, out of nothing. Most of the universes collapse to nothing, but a few that reach a critical size, will expand in an inflationary manner, and will form galaxies and stars, and maybe beings like us.
It has been a glorious time to be alive, and doing research in theoretical physics. Our picture of the universe has changed a great deal in the last 40 years, and I'm happy if I have made a small contribution. I want to share my excitement and enthusiasm. There's nothing like the Eureka moment, of discovering something that no one knew before.