
With many of us living a good chunk of our lives online it may seem as if reality has become a whole lot bigger over the last few decades. In one branch of theoretical physics, though, things seem to be going the other way. Over the last two decades string theorists have been developing the idea that the space and time we inhabit, including ourselves, might be nothing more than an illusion, a hologram conjured up by a reality which lacks a crucial feature of the world as we perceive it: the third dimension. Juan Maldacena, professor at the Institute for Advanced Study in Princeton, has played a vital role in the development of this idea, which is known as the holographic principle. In the 1990s Maldacena came up with the very first model of a universe which realises the holographic principle. Plus caught up with him on his recent visit to Cambridge.
Twentieth century mystery
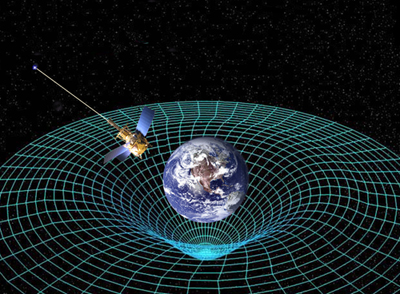
Massive bodies warp spacetime. Image courtesy NASA.
The holographic principle grew out one of the biggest scientific problems of the twentieth century: the fact that the two fundamental theories of physics, general relativity and quantum mechanics, don't get along with each other.
In the early twentieth century Einstein realised that space and time are inextricably linked, and he called the structure formed by both of them spacetime. His theory of general relativity states that spacetime is warped by massive objects and that gravity is a result of this warping. Just as a pool ball placed on a trampoline will create a dip that a nearby marble will roll into, so does a massive body like a planet distort spacetime, causing nearby objects to be attracted to it. Gravity, according to Einstein, isn't something that propagates through space, but a result of the very fabric of spacetime geometry.
While general relativity describes the world of planets and galaxies, quantum mechanics looks at the sub-atomic scale, the realm of the fundamental particles that make up matter. At these small scales, there's little mass and gravity is negligible. Quantum field theory, a quantum mechanical description of particle physics, holds that the fundamental forces work through messenger particles called gauge bosons: one fundamental particle exerts a force on another by sending over a few these gauge bosons.
In the course of the twentieth century, the messenger particles of three of the four fundamental forces, the electromagnetic force, the weak nuclear force and the strong nuclear force, have all been observed in experiments. To make things consistent, Einstein's theory of gravity should also be re-written in terms of similar messenger particles. Physicists have dubbed gravity's hypothetical messenger particle the graviton, but so far no-one has found a trace of it. What's worse, attempts to describe the graviton in terms of the mathematics of quantum field theory lead to non-sensical answers. "A naive quantisation of gravity doesn't work and leads to mathematical inconsistencies," says Maldacena. "We need something new."
Quantum mechanics describes the sub-atomic world remarkably well.
This new and hotly sought-after theory of quantum gravity has so far eluded physicists. One strong contender is string theory, or string theories, as it's really a collection of several logically consistent theories. The central idea of string theory is that fundamental particles are tiny vibrating strings, an approach that gets around the mathematical problems of a naive quantum gravity. It's a mathematical theory whose elegance has captured the hearts of many physicists. The downsides are that string theory does not as yet give a complete description of the world — there are many physical quantities it can't yet describe — and that it has not, and currently cannot, be tested. Nevertheless, it is string theory which handed Maldacena a clue to solving the quantum gravity riddle: by turning gravity into an illusion conjured up by a quantum hologram.
Black holograms
The conflict between general relativity and quantum mechanics poses no problem for most practical purposes, as physicists usually look at either the large-scale world, where quantum effects do not come into play, or at the small-scale world, where particles are light and gravity has little effect. But there is one situation in which the clash of the two theories is tangible: black holes are formed when a large amount of mass is concentrated in a tiny region of space. The resulting gravitational pull is so strong that nothing can escape from a black hole, not even light, so there's no way you can ignore gravity when thinking about black holes. The small scale means that quantum effects also come into play. To describe what's going on in a black hole, you really do need a unified theory of quantum gravity.
Black holes are also what first gave rise to the holographic principle. They come with a boundary of no return called the event horizon. Once you pass that horizon, you're sucked into the black hole, and you'll never get out again. When you fall into a black hole a lot of information goes with you. It's not just your DNA and one or two of your best ideas, but also the zillions of ways in which the blood cells in your veins could be configured and the complete jumble of thoughts in your mind. The black hole, for its part, seems a lot simpler. Assuming that nothing ever escapes from a black hole, classical physics says that a black hole can be completely described by just three bits of information: its mass, its electric charge and the speed at which it spins. Thus, when you fall into a black hole, all the information needed to describe you is subsumed by three numbers — your fall makes the Universe a little simpler.

A simulated black hole with the Milky Way in the background. Image courtesy Ute Kraus, Space Time Travel.
This kind of complexity loss tends to worry physicists, because it violates one of their most fundamental laws, the second law of thermodynamics. It states that things never, ever, get simpler. The amount of information needed to describe a system is measured by a quantity called entropy. Classically, entropy was defined for thermodynamic systems, for example an ice cube left out to melt in the Sun. Classical entropy measures to what extent heat (or energy) has dissipated through the system.
But since energy corresponds to excited atoms (in the frozen ice cube the water molecules are neatly arranged in a fixed lattice, while in liquid water they are buzzing around), entropy is also a measure of the disorder in the system. Disorder, in turn, is related to information: you can describe the regular arrangement of the molecules in a frozen ice cube in a sentence, but for liquid water you need to give the precise location of each individual molecule, and that's a lot of information. Entropy therefore works from a thermodynamic, as well as from an information point of view.
The second law says that entropy never decreases. In a thermodynamic situation this means that the system strives for an equilibrium where energy has dissipated completely. In an information context, this means that things don't become simpler of their own accord. In classical terms, a black hole, not being a thermal object and being extremely simple to describe, should have no entropy. When you fall in, your positive entropy is replaced by the zero entropy of the black hole. The second law of thermodynamics is violated.
When this potential breech was first noted, some physicists simply resigned themselves to the fact that the second law might not be that fundamental after all. But one person who wouldn't let go of it was Jacob Bekenstein. In 1972 Bekenstein picked up on a similarity between entropy and a property of black holes that had been discovered by Stephen Hawking. Hawking had been thinking about the event horizons of black holes. Just like the shell of an egg, the event horizon encloses a volume of space — it is a surface and you can measure its area. Hawking had shown that the surface area of the event horizon never, ever becomes smaller. Whatever you do to a black hole, whatever you throw in, the surface area of the event horizon can only ever increase — just like entropy.

The second law of thermodynamics paved the way for the holographic principle.
This analogy with thermodynamics was thought to be purely coincidental, but Bekenstein came up with a controversial interpretation: "Bekenstein noted that you could think of the area of the event horizon as a kind of entropy," explains Maldacena. "This idea was very vague at first, but it became clearer when Hawking discovered [in 1974] that black holes can emit energy [now known as Hawking radiation]." In other words, black holes are thermal objects, and therefore they do have entropy after all. "Combining Bekenstein's original idea with Hawking radiation, one can calculate that the entropy of a black hole is indeed equal to the area of the event horizon measured in a certain type of length scale, called the Planck unit. This is a very tiny distance, so the entropy of a macroscopic black hole is very large. " Although a black hole governs a three-dimensional volume of space, its information content seems to be a feature of its two-dimensional event horizon.
Real-life holography?
Well, black holes are weird, you might say, but the physicists Gerardus 't Hooft and Leonard Susskind went further by considering the information content of ordinary regions of space. Information manifests itself physically, whether it's in the pages of a book, the neurons in your brain, or the photons that whiz up and down fibreoptic cables transmitting information over the Internet. This physical manifestation involves energy. And since energy is equivalent to mass (recall Einstein's E=mc2), squeezing information into a confined region of space is akin to squeezing mass into it. If you try and squeeze too much mass/information into it, you form a black hole, so there's a limit to the information content of a confined region of space that's not a black hole. 'T Hooft and Susskind calculated this limit and found that, as with black holes, it is measured by the surface area of the region's boundary.
"This sounds like something very simple and innocent," says Maldacena, "but in all other descriptions we have of the world, the number of variables grows like the volume. For example, if we want to describe an electromagnetic field [in a region of space], we divide the volume into many pieces and describe the field in every piece." If you double the volume of your region, you double the number of pieces, so the amount of information you need for your description should also double: according to intuition, information should grow in line with volume, and not, as the holographic principle suggests, with surface area. If the holographic principle is true, then our three-dimensional approach to physics overshoots the mark. We should be able to get by with a leaner version, one that hinges on area, rather than volume. This raises the mind-numbing question of whether the third dimension is actually real, or merely an illusion, like the three-dimensional image created in a hologram.
So far, nobody has found a precise formulation of the 2D version of physics that describes our 3D world. However, in 1995 Susskind re-defined string theory with the holographic principle as a central pillar. And in 1997, at the tender age of 29, Juan Maldacena came up with the first ever concrete description of a holographic universe.
Negative curves
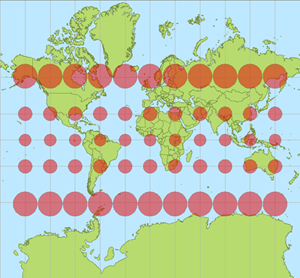
The Mercator projection of the Earth. The red discs actually have the same areas — their diferent sizes on the map illustrate the distortion of the map. Image courtesy Stefan Kuhn.
Maldacena's universe is not like the one we actually live in: it's a model, a toy universe, which comes complete with its own physics. It's a hologram because all the physical goings-on inside it can be described by a physical theory that's only defined on the boundary. What's more, it's a universe in which the gravity/quantum conundrum has been resolved completely: the boundary theory is purely quantum, it contains no gravity, but a being living in the interior will still experience gravity. Gravity in this universe is part of the holographic illusion.
To understand Maldacena's toy world, let's first take an excursion into the world of map-making. To represent the surface of the spherical globe on a flat piece of paper, you need to cut the sphere open and squeeze it down flat, and this inevitably creates some distortion. On the traditional Mercator projection of the Earth this distortion is worst near the poles. When you look at the map, Greenland appears as big as Africa, while in reality it is over 14 times smaller. Moreover, if you project the shortest route from, say, London to Sydney onto your map, you don't get a straight line, but a curve. On your map straight lines do not correspond to paths of shortest distance.

Circle Limit III by MC Escher. The paths of shortest distance are indicated in white.Image © 2009 The M.C. Escher Company - the Netherlands. All rights reserved. Used by permission.
A map of a two-dimensional version of Maldacena's universe is shown in the famous Circle Limit III woodcut by MC Escher. As with the Mercator projection, there is some distortion. The shortest path between two points inside Escher's map isn't along the straight line connecting them. Rather, it follows the arc of a circle which meets the boundary circle of the disc at right angles.
If you measure the size of the fish using this new metric, you'll find that, contrary to appearance, they do not get smaller and smaller as they get closer to the bounding circle, but are actually of equal size. Just as a traveller wandering on the face of the Earth will be unaware of the distortion indicated by Mercator's map, a being living inside this so-called hyperbolic world would never notice any distortion in the size of the fish. What's more, to get to the bounding circle, the hyperbolic being would have to traverse infinitely many copies of equally sized fish. In other words, it would have to cross an infinite distance. To the hyperbolic being, the boundary circle is infinitely far away, and it is blissfully unaware of it.
A representation of the "true" hyperbolic plane, one that isn't just a map of it, is almost impossible to draw because it is wildly twisted. It has what mathematicians call negative curvature. Very small regions of this "plane" look like saddles: along one direction, they look like the summit of a mountain ridge, and along another direction they look like the bottom of a valley.
To external observers like us, this strange two-dimensional world has an intriguing property: despite being infinite in extent (according to the new metric) we can observe its boundary — just what we need in order to apply the holographic principle, which describes the inside of a region of space in terms of its boundary. For his model universe, Maldacena used a three-dimensional analogue of the hyperbolic plane, coupled with a fourth dimension which serves as time. This model of four-dimensional spacetime is known as anti de Sitter space, after the Dutch physicist Willem de Sitter.
Toy physics
Anti de Sitter space is very different from the world we actually live in — both space and time are distorted in strange ways — but this shouldn't stop you from inventing some physics for it. All you need is a notion of the fundamental objects of this physics — fundamental particles and forces — and some mathematical laws describing their interaction. Maldacena used a version of string theory to describe the physics that happens in the interior of his model universe. As you'll recall, string theory includes both gravity and quantum mechanics, so a being living inside Maldacena's world will experience gravity in a similar way as we do.

A holographic Universe.
Maldacena's crucial observation was that the string theory describing the interior of his universe has a sort of "shadow" on the boundary of the universe: you can define a quantum field theory on the boundary so that every fundamental particle in the interior has its counterpart on the boundary, and so that every interaction between interior particles corresponds exactly to an interaction between boundary particles. You can now describe the action of, say, dropping an apple in the interior purely in terms of the boundary theory. You can even choose to ignore the interior altogether without losing any information at all — this world is a true hologram.
The important point from a quantum gravity angle is that the boundary theory is a well-understood quantum theory of particle physics, very similar to the one we use to describe sub-atomic processes in nature. Referring only to small scales, it doesn't bother with gravity. Yet it is able to describe the esoteric quantum gravity theory which governs the interior. It's the first ever complete description of a quantum spacetime.
But what does it mean for us?
As it stands, Maldacena's model is just that, a model. We do not yet know if the universe we live in is a hologram, and we still don't have a consistent quantum description of gravity that applies to our world. The negative curvature assumption in Maldacena's model is crucial, and our universe, as we know from observations, comes with a very slight positive curvature. "We don't know of a similar description for a situation with positive curvature," concedes Maldacena. "People have various ideas and they are being explored, but we don't have a complete answer yet."
But what if it turns out that the holographic principle does apply to the world we live in? Will this mean that we, along with spacetime, are just an illusion? "Yes, you could say [we are] an illusion, or an emergent phenomenon," says Maldacena. "If we lived in such a universe we would be, in some sense, approximate descriptions. But that's nothing new in physics. Take the surface of a lake, for example. It seems to be a well-defined surface, insects can walk on it. But if you look with a sufficiently powerful microscope, you'll see that there are molecules moving around and there is no sharply defined surface. The idea is that spacetime could be similar. It's not well-defined in an absolute sense, but we are so big that we don't notice it." Just like the insects on the lake, we'd be looking at the world with eyes that are too crude to reveal the true nature of spacetime. Ignorance is bliss, so in an every day practical sense, whether or not we live in a hologram probably doesn't really matter — though there's endless fun to be had with the philosophical side of things.
But what about Maldacena himself? Does he really believe that the holographic principle is true? "Well, I view this idea as a model, but it's a model that gives a mathematical description of quantum spacetime. So we should take it seriously until someone refutes it, or comes up with something better."
About this article
Juan Maldacena is a Professor at the Institute for Advanced Study in Princeton. He was interviewed by Marianne Freiberger, co-editor of Plus, in Cambridge in April 2009.