
On June 25th 1998 the Solar and Heliospheric Observatory known as SOHO, a small spacecraft that monitors the sun, went missing. An error in the instructions given to it from ground control left it spinning out of control. With its solar panels in shadow its battery ran down and it lost contact with Earth.

A false-colour picture of the sun taken by the Extreme ultraviolet Imaging Telescope (EIT) on SOHO (Courtesy of SOHO/EIT consortium. SOHO is a project of international cooperation between ESA and NASA.)
However, there is a glimmer of hope. It was likely that, as SOHO spinned, its solar panels would again point briefly towards the sun giving it just enough power to phone home. But how would SOHO's operators on Earth know which way to point their receivers? How do you find something that's lost in space?
Celestial Mechanics
Central to an understanding of spacecraft navigation is Newton's inverse square law of gravity.
![F=G*m[1]*m[2]/r^2](/issue6/xfile/gravity.gif)
Using this law we can write down equations which describe the motion of the sun, the planets and any spacecraft flying about between them. If we simplify the solar system and consider only the sun and the Earth we can solve the equations analytically. That means we can find a simple solution which predicts exactly where they'll be at any point in time given information about their positions and velocities at some starting point. This problem is known as the two body problem and the solutions describe the familiar eliptical orbits of the planets known since the time of Kepler.
Unfortunately, when we add a third body to our equations of motion, such as a spacecraft lost in space between the Earth and the sun, we can no longer find an analytical solution. The equations are unsolvable. This problem is known as the three body problem of celestial mechanics and remains the subject of research today.
Lagrange
Joseph-Louis Lagrange showed that there were at least some solutions to the three body problem if we restricted the three bodies to move in the same plane and assumed that the mass of one of them was so small as to be negligible. In his solutions, the three bodies move in unison, always maintaining the same positions relative to each other.
If we think of a two body system (like the simplified Earth and sun system considered above) then the points at which a third small body may be found are now known as the Lagrange points in his honour. It turns out that there are five of these (see diagram below).
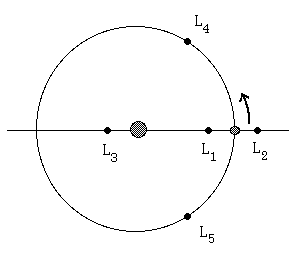
Although Lagrange probably never dreamed of man made spacecraft being "parked" at the points that bear his name this is precisely how they are used today. SOHO was orbiting the sun near L1, a good place for a spacecraft that studies the sun because it is never in the Earth's shadow and yet it can always "see" Earth closeby to beam back its findings. Unfortunately, L1 is only partially stable - objects placed there have a tendency to wander off if on-board rockets are not used to correct their position from time to time.
Searching for SOHO
Once SOHO was lost, the ground crew had to search space in the vicinity of L1 and find it before it wandered too far away. Fortunately, on 4th August 1998 their effort was rewarded and the slow rehabilitation of this tiny spacecraft, 1.5 million kilometers from Earth has now begun.
Further reading
For more information about SOHO see the SOHO Home page.
More information about Lagrange and his work on celestial mechanics is available from the "MacTutor history of mathematics archive":