What makes a perfect football? Anyone who plays or simply watches the game could quickly list the qualities. The ball must be perfectly round and retain its shape and internal pressure after a lot of physical abuse. It should be bouncy, but not too lively when kicked or headed and it must not absorb water. And finally it should move about in a pacey manner when passed between the players and be capable of impressive turns of speed for shots at goal.
This last point may seem trivial: surely footballs go faster the harder they're kicked? This is broadly true, but how much of this initial speed is retained in flight depends critically on what happens as air flows around the ball's surface. Probably more research is devoted to this factor than any other aspect of the ball's design. To see, why let's take a look at some wind tunnel images, what aerodynamicists refer to as flow visualisations.
Flow separation and the drag crisis
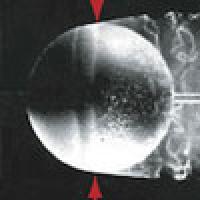
The image below shows a model ball mounted in a wind tunnel. The ball is stationary but by varying the speed of the airflow around it we can mimic what happens when the ball is in flight. Flow patterns are made visible by introducing a little smoke into the airstream.
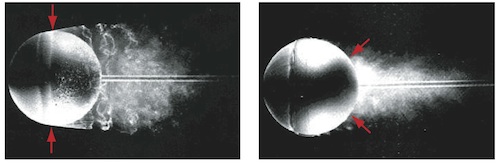
Flow separation and transition points for a model ball in a wind tunnel. The image on the left shows early separation and high drag while that on the right shows late separation and low drag. (Images by Henri Werlé, copyright Onera, the French Aerospace Lab)
At very low speeds the flow follows the surface of the ball intimately but as the speed is increased, as in the image on the left, the flow begins to break away at the aptly named separation points (indicated by the arrows). Note that when separation occurs at lowish speeds there is a very large turbulent region behind the ball, clearly visible in the image. Turbulence is the agency that causes aerodynamic drag, effectively robbing the ball of kinetic energy.
However, when the speed is increased even more a surprising thing happens. The separation points move towards the rear of the ball (as in the image on the right) and the flow clings to the surface once more. Downstream turbulence is greatly reduced, implying a significant reduction in aerodynamic drag. This transition is very sudden and is enormously important in ball games. The agency causing this is surface roughness and it is very counter-intuitive that a slightly rough surface should have a superior aerodynamic performance compared with a smooth one.
Aerodynamic drag can be measured very precisely by using sensitive instruments attached to the rig on which the ball is mounted. The drag force F is then characterised using a simple expression $$ F=\frac{1}{2} C_d \rho A V^2. $$ Here $\rho$ is the density of air, $A$ the cross-sectional area of the ball and $V$ its speed (or the speed of the air flow in the wind tunnel). The parameter $C_d$ is the drag coefficient, a pure number that scales the strength of the drag force at a given speed. (You can read more about how this expression describes drag force in If you can't bend it, model it.)
Knowing the variation of $C_d$ with speed is very important in ball design and determining its value is quite simple: $F$ is measured at various speeds then $C_d$ is calculated from the above expression. This graph shows some experimental results obtained in this way for the classic 32–panel ball (a surface pattern of 12 pentagons and 20 hexagons) (by researchers in Japan) and for a smooth ball (by researchers in Germany).
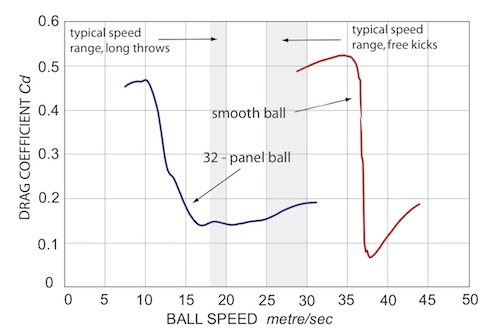
Variations in the drag coefficient Cd with different ball speeds. The typical speed ranges for long throws and free kicks are shown in the shaded regions.
The switch from high to low $C_d$ at some critical speed is very sudden and for this reason the transition is often referred to as the drag crisis. Notice also in this graph that the switch for the 32-panel ball occurs at a much lower speed than that for a smooth ball, about 12 metres per second (27 miles per hour) compared with 37 metres per second (83 miles per hour). This is very fortunate as most of the important actions in football such as long throw-ins, corners and free kicks take place within the low drag regime after this switch occurs.
As already noted, surface roughening is responsible for this important transition and it was not realised for many years that the stitched seams between the ball's panels produced just the right degree of aerodynamic roughness to do the trick. In fact it would be almost physically impossible to play a decent game of football with a perfectly smooth ball since only in very exceptional circumstances would it move fast enough to avert the drag crisis.
To illustrate this point I have modelled free kicks taken with the 32-panel ball and a smooth ball using the $C_d$ data shown in the graph above. The trajectories were obtained using the flight equations described in If you can't bend it, model it and represent fairly typical initial conditions: a kicking speed of 26 metres per second and a free kick distance of 22 metres.
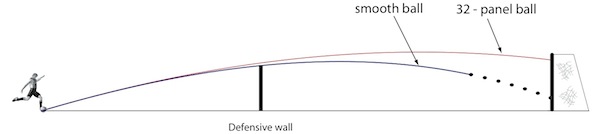
Figure 3: Free kicks with 32-panel ball and a smooth ball
The shot with the 32-panel ball would be challenging for a goalkeeper, reaching the goal after just 0.97 seconds. At this point the smooth ball still has 3.5 metres to go and would cross the goal line just under a quarter of a second later. Given its height at this point it would represent an easy save for a competent goalie. Looking at the ball speeds when the goal line is reached is even more revealing. The 32-panel ball is moving at 21 metres per second, compared with a speed of only 14.5 metres per second for the smooth ball. Aerodynamic drag has robbed the conventional ball of 35% of its initial kinetic energy. The equivalent figure for the smooth ball is 70%!
So seams and panels are important and it would be useful to know exactly how much seam there is on a modern ball.
Enter the fly
Let's imagine that we persuade a friendly fly to walk around the seam of a 32-panel ball, recording the distance it travels. We give the fly careful instructions: walk once and once only along each length of seam. It sets off and initially all goes well. But then the fly pauses and a horrible thought occurs: suppose our instructions about not crossing any length of seam twice have been taken too literally and the fly has begun to think about the Königsberg bridges problem. We could be here for years! But the fly sets off once more and we notice that it walks once around the perimeter of one of the hexagons and does the same for one of the pentagons. Then without telling us the answer it flies off and buzzes annoyingly, as flies do, on the window pane.
There's obviously a neat solution to this problem and a little thought reveals the fly's reasoning. Each side of each pentagon or hexagon is shared with its neighbour. So if we calculate the total perimeter of all the hexagons and pentagons and divide by two we'll have our answer. There are 20 hexagons and 12 pentagons so the combined perimeters add up to $6\times 20+5 \times 12=180$ sides and dividing by two gives us 90 individual portions of seam. The total length of seams on the ball, $L$, is just $$ L=90s $$ where $s$ is the length of each side of a hexagon or pentagon. At this point we might simply measure $s$ using a classic 32-panel ball inflated to the correct pressure. But we can stretch our calculation a little further. The surface areas of regular pentagons and hexagons are given by $$ A_p=\frac{\sqrt{25+10\sqrt{5}}}{4}s^2 $$ and $$ A_h=\frac{3\sqrt{3}}{2}s^2 $$ respectively. Taking the radius of our ball to be $R$ (exactly 0.11m for a decent football) we have to a good approximation $$ 20A_h+12A_p=4\pi R^2. $$ This gives us a simple equation for $s$ and solving it we find $s$ = 4.58 centimetres. Now we can check using a real ball. Careful measurement of 10 portions of seam and averaging gives us a length of 4.57 centimetres — very satisfactory. Finally then, we find that the total length of seam is $L$ = 90$s$ = 4.12 metres.
In fact this result could have been achieved without the fly's aid, by making use of a famous expression first obtained by the Swiss mathematician Leonhard Euler. Ignoring its surface curvature the 32-panel ball corresponds to a truncated icosahedron, one of the 13 classic polyhedra known as the Archimedean solids. These have panels (or faces to use the conventional descriptor) made up of regular polygons, such as triangles, squares, pentagons, etc. The full set can be seen on Wikipedia and a selection is shown below.
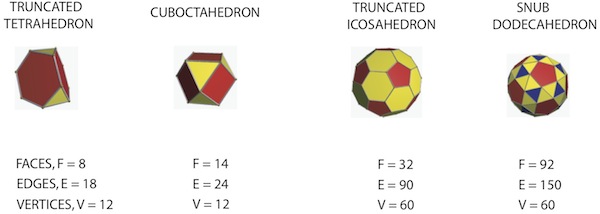
Selection of Archimedean solids (Images created by Robert Webb's Great Stella software)
For these objects Euler's formula states V + F - E = 2, where E and F are the numbers of edges and faces (seam lengths and panels) and V is the number of corners, called vertices, of the solid. (You can find out more in the article Euler's polyhedron formula.)
So if we required a ball with even greater seam length, the monster known as the snub dodecahedron could be used. Counting the faces (80 triangles, 12 pentagons!) and the vertices (60) we find from Euler's formula that the number of edges is 150. Then by repeating the calculation described above it turns out that the snub dodecahedron soccer ball would have a total seam length of very nearly 9.5 metres. Of course no manufacturer would make such a ball: joining 92 panels accurately would be far too fiddly a process and in any case, the 32-panel ball performs perfectly well. But how far might one go in the other direction, that is, fewer panels and correspondingly shorter overall seam length, and what problems might occur?
Fewer panels make a smoother ball
We could look at the relationship between panels and seam lengths by studying the Archimedean solids once more. As we've seen Euler's formula makes it particularly easy to relate these variables. A glance at the Archimedian solids above, however, shows that there's nothing resembling a football much below the 32-panel case. It would be easy to construct a "ball" based on the truncated tetrahedron (eight panels) with exactly the same surface area as its official counterpart: but there wouldn't be much fun involved in kicking this around the pitch. The image below suggests a way in which the problem might be explored, albeit for particularly simple footballs. All of the panel patterns are formed by regular arcs drawn from the centre of the ball so calculation of seam lengths is a simple matter.
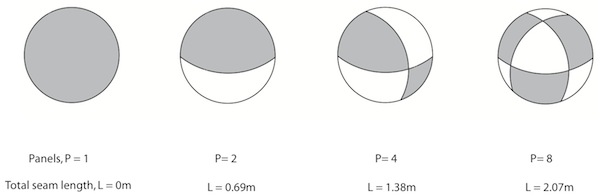
Simple panel structures and associated total seam lengths (ball radius = 0.11m)
It is easily found that two panels produce a total seam length of 0.69 metres, only 17% of that for the 32-panel ball and the length for the eight-panel ball is 2.07 metres (50%). Reducing the number of panels produces much less implicit surface roughening and that's the problem. A smoother surface might not be the cleverest design objective for a modern ball. And yet since 2006 this has been the driving force with panel numbers tumbling from 32 to 14 for the 2006 World Cup and then to only eight for the World Cup held in South Africa in 2010.
Pimples, grooves and knuckleballs

Teamgeist 2006 World Cup ball with14-panel structure
At the 2006 World Cup goalkeepers complained bitterly about the unpredictable movement of the Teamgeist (German, meaning "team spirit"), the ball specially designed by the sports manufacturer Adidas for the competition. The 32-panel format, used for every World Cup since 1970, was replaced by a radical new design with just 14 panels bonded into a continuous surface with artificial seams representing the formerly stitched seams at the panel boundaries. A glance at the Teamgeist ball, on the right, indicates the complexity of the panel shapes. These were pre-formed to follow a spherical curvature and the ball was proudly advertised as the "roundest" object ever to have been kicked around a pitch. As we have seen, however, reducing the number of panels has important implications for the total seam length and the implicit roughness of the surface.

Europass 2008 Euro Championships ball with panel pimpling
The problems were revealed when the ball was kicked fast with very little spin. Then, as individual portions of the seam rotated into the airflow the flow separation points (such as those shown in the wind tunnel images shown above) switched positions and the ball bobbed about erratically. This movement came to be known as "knuckling", a baseball term referring to a pitcher's attempt to throw the ball with scarcely any spin (you can read more in Eye on the ball). The very limited seam structure of a baseball (two panels, one seam) practically guarantees aerodynamic instability, and the knuckleball's unpredictable movement is very testing for batters in baseball.
A quick fix was applied by Adidas for Euro 2008, the UEFA European Championships. The competition ball, the "Europass" appeared with a rash of small pimples covering the previously smooth panels of the Teamgeist. This artificial roughening was intended to produce aerodynamic stability, but for the World Cup held in South Africa in 2010 things changed again.

Jabulani 2010 World Cup ball. Eight panels and aerodynamic grooves (Image by Cliff Cheng LF)
That ball, the Jabulani (Zulu, meaning "to celebrate") had only eight panels so surface texturing was a must. Instead of pimples the panels were covered with an intricate pattern of very fine surface depressions. Adidas called this "grip and groove" technology, implying that goalkeepers would find the ball easier to catch and hold. More cynical goalies, unconvinced that knuckleballs were a thing of the past, swiftly re-dubbed this "slip and move". In fairness to its designers the Jabulani appears to behave more stably in flight than the Teamgeist. But two things seem certain. For major tournaments there will be no return to the multiple panel formats of the past; in fact, we might expect even fewer panels than the eight of the present day. And necessarily, careful surface texturing will be needed to compensate for the seam roughening lost as a consequence.
Are panels a thing of the past?
The next opportunity to study developments in ball design will occur at the Olympic Games (where both men's and women's teams will compete) and at the Euro football Championships. Both events will be held in summer 2012. Two years on from the last World Cup is probably too short a time for radical changes in ball design but there is an intriguing parallel. Thirty years ago Gordon Moore, co-founder of computer chip manufacturer Intel, predicted that computing power would increase exponentially with time, since the number of transistors on a microchip was expected to double every two years. This prediction – Moore's Law – has proved remarkably prescient and we might argue that ball design is a kind of inverse of Moore's Law. Since 2002, panel numbers have roughly halved every four years: 32 in 2002, 14 in 2006 and eight in 2010. Thus, by the 2022 World Cup, players should be kicking a single-panel ball around the pitch. This will have a surface covered with a complex pattern of dimples and the football will finally resemble its little (but technically refined) brother, the golf ball.
Actually, given the pace of technology improvements, a decade seems too long. So, for the 2022 World Cup in Qatar, we confidently predict that there will be a single-panel ball whose aerodynamic performance will be impeccable. It will be called األوح د, (Arabic, al-awhad meaning "single", or "the one") and goalkeepers will love it. Remember, you saw it first in Plus!
About the author

Ken Bray is a theoretical physicist and a Senior Visiting Fellow in the Department of Mechanical Engineering at the University of Bath. His first book How to Score - science and the beautiful game was published by Granta in 2006 and is reviewed in Plus.