In the latest poll of our Science fiction, science fact project you told us that you wanted to know an answer to this question. So we went to speak to Francesca Vidotto and George Ellis to find out. Click here to see other articles exploring this question.

You are here

Space is the stage on which physics happens. If you are the lucky owner of a smartphone you can easily find out where on this stage you are right now, in global coordinates readily understood by any other GPS device on the planet. And once you start to move, the change in those coordinates describes your journey. Space itself has nothing to do with it: it could not care less about where you, or anything else in it, happens to be. And it would still be there even if everything else suddenly vanished.

A GPS satellite. If it, the Earth and everything else vanished, would space still it exist? Image courtesy NASA.

This is how we learn to think of space at school — a rigid box in which things happen — and it is hard to imagine it otherwise. Yet the idea only became mainstream recently, in historical terms, with Newton's Principia Mathematica published in 1687. "Absolute, true, and mathematical space remains similar and immovable without relation to anything external," he wrote.

Newton did not claim he could prove that physical space was really like that. "He was aware that [his statement] was just a hypothesis," says Francesca Vidotto, a theoretical physicist at the Radboud University Nijmegen. "But the assumption is so powerful, it allowed Newton to construct his mechanics; we can construct bridges, we can go to space and even outer space. Newton's assumption was so successful that people forgot it was only a hypothesis." Because of its power Newton's pronouncement pretty much put a lid on centuries' worth of philosophical debate on whether this abstract and relation-less space, this void, could actually exist in nature.

The space between your fingers

The maths that has grown from Newton's assumption, and which has given us bridges and spacecraft, is based on another idea that chimes with our intuition: that space is continuous. In theory you could zoom in on it to any level you like without seeing it break up into pixels or fall apart in some other strange way.

Yet from another point of view, the idea of continuity is itself pretty mind-boggling. A continuous piece of line, no matter how short, is made up of infinitely many individual points. There are so many points you could not even label them 1,2,3, ... as you could label an infinitely long queue of people if you had an infinite amount of time. A continuous line gives you an uncountable infinity, something inherently larger than an infinite amount of discrete objects. So assuming that space is continuous means admitting that you can hold a frighteningly large infinity in the palm of your hand.

"Suppose you hold your fingers ten centimetres apart," argues George Ellis, a cosmologist and mathematician at the University of Cape Town. "If you believe that there is a [continuous] line of points between those fingers, then you believe that there is an uncountable infinity of points between your fingers. That's completely unreasonable. I believe that that's a mathematical idea that does not correspond to physics."

Space warp

And it seems that Ellis may be right. The first blow to Newton's absolute space came in the early twentieth century when Einstein's theory of relativity turned it from a stage into one of the actors. Einstein realised that your measurement of time and distance can be influenced by how you move through space, so space and time are inextricably linked in what he called spacetime. He also realised that this spacetime can be curved. Gravity, previously thought of as an attractive force acting instantaneously across space, then became a consequence of spacetime geometry. Massive objects, like the Sun, curve and warp the very fabric of spacetime and this curvature diverts the paths of less massive objects in the vicinity — just like the path of a marble rolling around a surface is directed by the bumps and curves of that surface.

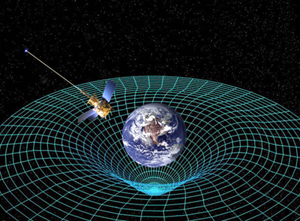
According to Einstein's general theory of relativity, massive objects curve spacetime. Image courtesy NASA.

When a lot of mass is concentrated in a very small region of space, which can happen, for example, when a massive star collapses in on itself, spacetime can curve so much that a black hole forms. The gravitational pull of the mass, the warping of spacetime, becomes so extreme that nothing, not even light, can escape from its vicinity. This means that there's no way of ever seeing inside a black hole from the outside, or of going in and coming back out again to report what you've seen — whatever happens in there, it is hidden from view.

Balls and waves

The other great development of early twentieth century physics, quantum mechanics, describes the tiniest building blocks of matter. It is based on the counter-intuitive idea that little particles, like electrons, behave like tiny little billiard balls at some times and like waves at others: they behave like a hybrid of the two. A consequence is Heisenberg’s famous uncertainty principle. Suppose you have such a "particle" and you’re interested in its position and its momentum (momentum is the particle’s mass times its velocity). The uncertainty principle says that the more precise you are about the particle’s position the less precise you can be about its momentum and vice versa. If you pin down, say, momentum to a good degree of accuracy your uncertainty about position increases. It’s not that the particle is somewhere definite but you just don’t know where, rather the particle is, in some sense, in many locations at once. Writing for the uncertainty in position and for the uncertainty in momentum, the principle is encapsulated by the inequality

Here is a constant named after the physicist Max Planck. It’s an incredibly small number,

but still, the inequality shows that and cannot simultaneously become arbitrarily small.

The smallest length

Something curious happens when you try to combine quantum mechanics with relativity. To explore a region of space you need to send in a probing particle (typically a photon, a particle of light) and observe how that scatters off whatever objects are inside the region. Now if the region is tiny, with a very small diameter , then as a consequence of Heisenberg’s uncertainty principle your probing particle’s momentum is "spread" over a large range which includes very large momenta. But a large momentum means a lot of energy and energy is related to mass by Einstein’s famous equation

where is energy, mass and the speed of light.

So localising a particle in a very small region means concentrating a lot of mass there. If the region is sufficiently small — if is below a certain critical value — then the mass of the probing particle is so great that a black hole forms and swallows both and whatever is inside it. The crucial size is given by something called the Planck length: it’s metres. This is unimaginably small, but nevertheless it’s not zero, so anything sufficiently small is, according to this thought experiment, forever hidden from view.

What happens to space at the smallest scale?

"This tells us that below the Planck scale it makes no sense to talk about distances and length," says Vidotto. But does it mean that we just can't see anything smaller than the Planck length, or that something smaller does not exist? "In my opinion you can view this as a fundamental thing," says Vidotto. "You can think about [this] as the discovery that there is nothing below the Planck length."

As a consequence space itself can be thought of as made up of individual units, of Planck-length "atoms"; you simply can't zoom in on it any closer. "I think we have good reason to believe that spacetime is made of atoms," says Ellis. "If you hold your fingers those 10cm apart, there is a large number of physical points between them, but not an infinity of them."

The reasoning that gave us the shortest length came from a naive attempt to combine relativity with quantum mechanics. It turns out, however, that such a naive attempt soon runs into trouble, giving rise to contradictions and non-sensical predictions. Physicists have not yet found a fully-fledged theory of quantum gravity. There are exotic contenders, for example string theory and loop quantum gravity. "String theory and loop quantum gravity agree that there is this fundamental scale," says Vidotto. "But there are other approaches which don't exploit this [idea]."

But can we test the idea experimentally? "First of all we should be clear that short means really short," says Vidotto. "There is the same ratio between our size and the size of a proton as there is between the size of a proton and the Planck length. It is tiny." Probing anything approaching the Planck length requires energies that go way beyond what current technology permits.

"I think that if one day we will see the signature of the discreteness of spacetime this will be in cosmology," says Vidotto. "Such discreteness may have left a small imprint in the cosmic microwave background [the left-over radiation from the Big Bang] from which we extract information about the seeds of the structures that we observe in the Universe today; stars, galaxies, clusters of galaxies and so on. Maybe one day we will be able to understand how these seeds arose as a direct result of quantum discreteness."

There is also a remote possibility that help may come from the other end of the Universe. The supposed atomic structure of spacetime may modify the speed of light. By observing light that has travelled across vast distances from the furthest reaches of the visible Universe, we may be able to detect the resulting time delay. "We have the technology to do this," says Vidotto. "A few years ago the MAGIC telescope did measure such a time delay." But one measurement is not sufficient to draw hard and fast conclusions, especially since the physical processes involved are not yet fully understood.

But even if the atomic nature of spacetime will one day be confirmed, in everyday life it's safe to stick to our Newtonian intuition. As a description of nature, Newton's physics is only approximately true, but it's an approximation that works perfectly well for the size and time scales we are used to dealing with. As Vidotto puts it, "the job of a good physicst is to apply the right physics to the right regime".

About this article

Marianne Freiberger is Editor of Plus. She interviewed Francesca Vidotto and George Ellis in Cambridge in March 2013.