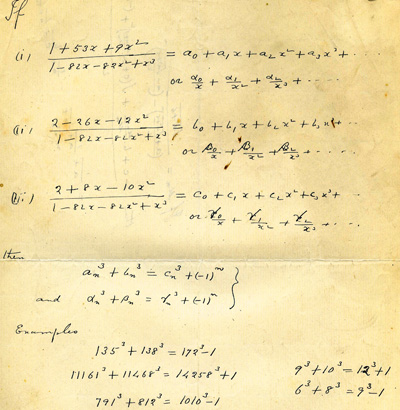
Ramanujan's manuscript. The representations of 1729 as the sum of two cubes appear in the bottom right corner. The equation expressing the near counter examples to Fermat's last theorem appears further up: α3 + β3 = γ3 + (-1)n. Image courtesy Trinity College library. Click here to see a larger image.
A box of manuscripts and three notebooks. That's all that's left of the work of Srinivasa Ramanujan, an Indian mathematician who lived his remarkable but short life around the beginning of the twentieth century. Yet, that small stash of mathematical legacy still yields surprises. Two mathematicians of Emory University, Ken Ono and Sarah Trebat-Leder, have recently made a fascinating discovery within its yellowed pages. It shows that Ramanujan was further ahead of his time than anyone had expected, and provides a beautiful link between several milestones in the history of mathematics. And it all goes back to the innocuous-looking number 1729.
Ramanujan's story is as inspiring as it is tragic. Born in 1887 in a small village around 400 km from Madras (now Chennai), Ramanujan developed a passion for mathematics at a young age, but had to pursue it mostly alone and in poverty. Until, in 1913, he decided to write a letter to the famous Cambridge number theorist G.H. Hardy. Accustomed to this early form of spam, Hardy might have been forgiven for dispatching the highly unorthodox letter straight to the bin. But he didn't. Recognising the author's genius, Hardy invited Ramanujan to Cambridge, where he arrived in 1914. Over the following years, Ramanujan more than repaid Hardy's faith in his talent, but suffered ill health due, in part, to the grizzly English climate and food. Ramanujan returned to India in 1919, still feeble, and died the following year, aged only 32. Hardy later described his collaboration with Ramanujan as "the one romantic incident in my life".
The taxi-cab number
The romanticism rubbed off on the number 1729, which plays a central role in the Hardy-Ramanujan story. "I remember once going to see [Ramanujan] when he was ill at Putney," Hardy wrote later. "I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavourable omen. 'No', he replied, 'it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways.'" What Ramanujan meant is that $$1729 = 1^3 + 12^3 = 9^3 + 10^3.$$
The anecdote gained the number 1729 fame in mathematical circles, but until recently people believed its curious property was just another random fact Ramanujan carried about in his brain — much like a train spotter remembers train arrival times. What Ono and Trebat-Leder's discovery shows, however, is that it was just the tip of an ice berg. In reality Ramanujan had been busy developing a theory that was several decades ahead of its time and yields results that are interesting to mathematicians even today. He just didn't live long enough to publish it.
The discovery came when Ono and fellow mathematician Andrew Granville were leafing through Ramanujan's manuscripts, kept at the Wren Library at Trinity College, Cambridge. "We were sitting right next to the librarian's desk, flipping page by page through the Ramanujan box," recalls Ono. "We came across this one page which had on it the two representations of 1729 [as the sum of cubes]. We started laughing immediately."
Fermat's last theorem and near misses

Srinivasa Ramanujan (1887 - 1920).
Ono and Granville spotted the famous number even though it didn't itself appear on the page. Ramanujan had only written down the equation $1^3 + 12^3 = 9^3 + 10^3.$ But what delighted the two mathematicians more than meeting the famous number in disguise was another equation appearing on the same page. It clearly showed that Ramanujan had been working on a problem that had become notorious way back in the 17th century and whose solution, in the 1990s, was a major mathematical sensation. It's known as Fermat's last theorem.
The problem, like so many problems in number theory, is easy to understand. Pythagoras' theorem tells us that if a right-angled triangle has sides of lengths $x,$ $y$ and $z,$ with $z$ being the longest side, then the three lengths satisfy the equation $$x^2+y^2=z^2.$$ There are infinitely triples of positive whole numbers $x,$ $y$ and $z,$ which satisfy this relationship. An example is $x=3,$ $y=4$ and $z=5.$ A natural question is whether you can also find three positive whole numbers (excluding 0s) satisfying the equationIn 1637 the French mathematician Pierre de Fermat confidently asserted that the answer is no. If $n$ is a whole number greater than $2,$ then there are no positive whole number triples $x,$ $y$ and $z,$ such that
$$x^n+y^n=z^n.$$ Fermat scribbled in the margin of a page in a book that he had "discovered a truly marvellous proof of this, which this margin is too narrow to contain". Naturally, this assertion was like catnip to mathematicians, who subsequently drove themselves crazy, for over 350 years, trying to find this "truly marvellous proof". What the equation in Ramanujan's manuscript illustrates is that Ramanujan had found a whole family (in fact an infinite family) of positive whole number triples $x,$ $y$ and $z$ that very nearly, but not quite, satisfy Fermat's famous equation for $n=3.$ They are off only by plus or minus one, that is, either $$x^3+y^3=z^3 + 1$$ or $$x^3+y^3=z^3 - 1.$$ Since any positive whole number triple satisfying the equation would render Fermat's assertion (that there are no such triples) false, Ramanujan had pinned down an infinite family of near-misses of what would be \emph{counter-examples} to Fermat's last theorem."None of us had any idea that Ramanujan was thinking about anything [remotely] related to Fermat's last theorem," says Ono. "But here on a page, staring us in the face, were infinitely many near counter-examples to it, two of which happen to be related to 1729. We were floored." Even today, nearly 400 years after Fermat's claim and 20 years after its resolution, only a handful of mathematicians even know about the family Ramanujan had come up with. "I'm a Ramanujan scholar and I wasn't aware of it," says Ono. "Basically, nobody knew."
Elliptic curves and climbing K3.
But this isn't all. When Ono and his graduate student Sarah Trebat-Leder decided to investigate further, looking at other pages in Ramanujan's work, they found he had developed a sophisticated mathematical theory that went beyond anything people had suspected. "Sarah and I spent time thinking more deeply about what Ramanujan had really done, and it turns out that he anticipated [an area of] mathematic 30 or 40 years before anyone knew this field would exist. That's what we are excited about."
It turns out that from looking at equations of the form $$x^3 + y^3 = z^3$$ it's not too large a mathematical step to considering equations of the form $$y^2 = x^3 + ax +b,$$
where $a$ and $b$ are constants. If you plot the points $(x,y)$ that satisfy such an equation (for given values of $a$ and $b$) in a coordinate system, you get a shape called an \emph{elliptic curve} (the precise definition is slightly more involved, see here). Elliptic curves played an important role in the eventual proof of Fermat's last theorem, which was delivered in the 1990s by the mathematician Andrew Wiles.
Ono and Trebat-Leder found that Ramanujan had also delved into the theory of elliptic curves. He did not anticipate the path taken by Wiles, but instead discovered an object that is more complicated than elliptic curves. When objects of this kind were rediscovered around forty years later they were adorned with the name of K3 surfaces — in honour of the mathematicians Ernst Kummer, Erich Kähler and Kunihiko Kodaira, and the mountain K2, which is as difficult to climb as K3 surfaces are difficult to handle mathematically.
That Ramanujan should have discovered and understood an exceedingly complicated K3 surface is in itself remarkable. But his work on the surface also provided an unexpected gift to Ono and Trebat-Leder, which links back to elliptic curves. Like all equations, any elliptic curve equation $$y^2 = x^3 + ax +b,$$ naturally cries out for solutions: pairs of numbers $(x,y)$ that satisfy the equation. In the spirit of Fermat, you might look for whole number solutions, but number theorists usually give themselves a little more leeway. They look for solutions that are \emph{rational numbers}, that is, numbers that can be written as fractions.
The elliptic curves corresponding to whole number values of a between -2 and 1 and whole number values of values of b between -1 and 2. Only the curve for a = b = 0 doesn't qualify as an elliptic curve because it has a sharp corner.
Last year, in 2014, the mathematician Manjul Bhargava won the Fields Medal, one of the highest honours in mathematics, for major progress in this context. Bhargava showed that most elliptic curves fall into one of two particularly simple classes. Either there are only finitely many rational number solutions; or there are infinitely many, but there is a recipe that produces all of them from just a single rational number solution. (You can read our interview with Bhargava and our article exploring some of his work.)
If you sift through all elliptic curves in a systematic way, for example by ordering them according to the size of the constants $a$ and $b$ that appear in their formulas, then you are most likely only ever going to come across these "simple" elliptic curves. The probability of finding a more complicated one, which requires two or three solutions to generate them all, is zero. Searching for such elliptic curves systematically is like searching a haystack for a needle in a way that guarantees the needle will always slip through the net. To get at those more complicated elliptic curves, you need another method.And this is exactly what Ramanujan came up with. His work on the K3 surface he discovered provided Ono and Trebat-Leder with a method to produce, not just one, but infinitely many elliptic curves requiring two or three solutions to generate all other solutions. It's not the first method that has been found, but it required no effort. "We tied the world record on the problem [of finding such elliptic curves], but we didn't have to do any heavy lifting," says Ono. "We did next to nothing, except recognise what Ramanujan did."
Physics and extra dimensions
There is another interesting twist to this story. While Ramanujan was working in the abstract realms of number theory, physicists studying real-world phenomena began developing the theory of quantum mechanics. Although a triumph in its own right, it soon became clear that the resulting quantum physics clashed with existing physical theories in an unredeemable way. The rift still hasn't been healed and presents the biggest problem of twenty-first century physics (see here to find out more). One attempt at rescuing the situation was the development, started in the 1960s, of string theory, a prime candidate for a "theory of everything" uniting the disparate strands of modern physics.

G.H. Hardy (1877 - 1947).
A curious prediction of string theory is that the world we live in consists of more than the three spatial dimensions we can see. The extra dimensions, the ones we can't see, are rolled up tightly in tiny little spaces too small for us to perceive. The theory dictates that those tiny little spaces have a particular geometric structure. There's a class of geometric objects, called Calabi-Yau manifolds, which fits the bill (see this article to find out more). And one of the simplest classes of Calabi-Yau manifolds comes from, wait for it, K3 surfaces, which Ramanujan was the first to discover.
Ramanujan could never have dreamt of this development, of course. "He was a whiz with formulas and I think [his aim was] to construct those near counter-examples to Fermat's last theorem." says Ono. "So he developed a theory to find these near misses, without recognising that the machine he was building, those formulas that he was writing down, would be useful for anyone, ever, in the future."
Ono doesn't rule out that Ramanujan's manuscripts contain further hidden treasures. "I've known about 1729 for thirty years. It's a lovely, romantic number. Ramanujan was a genius and we are still learning about the extent to which his creativity led him to his formulas. His work amounts to one box, kept at Trinity College, and three notebooks, kept at the University of Madras. That's not a lot. It's crazy that we are still figuring out what he had in mind. When is it going to end?"
Further reading
You can read more about the work of Ramanujan in A disappearing number. For experts, Ono and Trebat-Leder's paper is available here.
About this article
Ken Ono is Asa Griggs Candler Professor of Mathematics and Computer Science at Emory University.
Sarah Trebat-Leder is a PhD student at Emory, where she is a Woodruff Fellow and NSF Graduate Fellow.
Marianne Freiberger is Editor of Plus. She interviewed Ono and Trebat-Leder in October 2015.
This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
