
Answers on a donut – the Fields medal lecture of Manjul Bhargava
When Manjul Bhargava gave his Fields medal lecture at the 2014 International Congress of Mathematicians in Seoul on Saturday, a rare and exciting thing happened: everyone in the audience was able to understand it, even non-specialists like ourselves.

This sounds like a trivial thing, or even a criticism of mathematicians, but it is not. When experts are explaining very recent results at the cutting edge of their field to fellow mathematicians, they can't start at the beginning if they are going to finish their talk in one hour. Instead, they assume certain amounts of knowledge and certain amounts of fluency in the terminology in order to have time to get to the juiciest parts of their work.
But, thanks to his brilliance at explanation and presentation, and the slighty less daunting language of number theory, Bhargava took us all the way from Egyptian solutions of Pythagorus' theorem in the form of their built stone structures to results he and colleagues proved just a month ago. We enjoyed it so much we wanted to share it with you – so here is an abridged version of his Fields medal lecture, as seen by Plus!
A very old question
Bhargava's talk was in essence about a very classical question that has been part of maths for thousands of years and plays a particularly important role in number theory: when is a mathematical expression a square number?
The earliest examples seem to be the megolithic structures built over three thousand years ago in Egypt and Northern Europe. These contain right-angled triangles whose side lengths were integer multiples of commonly used measures of distance. This implies, says Bhargava, that not only were these people able to solve the equation $$ c^2=a^2+b^2 $$ over 3000 years ago, but that they found many whole number solutions for $a$, $b$ and $c$ (called pythagorean triples) as the answers were constructed in stone!
Similar questions have been a part of mathematics ever since. A more recent example was a result from 1913 when the brilliant Indian mathematician Srinivasa Ramanujan proposed that the value of the expression $$ 2^n -7 $$ is a squared number (that is, it is equal to $y^2$ for some integer $y$) when $n=3, 4, 5,7$ and $15$, and for no other values of $n$.
This very surprising fact was finally proved some years later in 1948. In fact we now know that the expression $$ 2^n-b $$ for a particular $b$ is a square number for only at most 2 values of $n$. The only exception is when $b=7$ which is a square number for the five values of $n$ that Ramanujan found over 30 years earlier.
Today, Bhargava says, we would ask different types of questions. Instead of asking what happens for a particular equation of this form, say for a particular value of $b$, today mathematicians ask what would happen for a typical equation of this type? We know that for any such expression there are at most 2 values of $n$ that give a square number. But is this usually the case? Or perhaps, for most expressions of this type are there usually no values of $n$ that work?
Hyperelliptic curves – not as scary as they sound
Bhargava, reassuringly, said that the rest of his talk would be about the simplest kind of square equations. Although these have the daunting name of hyperelliptic curves they are simply polynomials over $x$ (a sum of various multiples of powers of $x$) that are square numbers: $$ y^2 = f(x) = a_0x^n + a_1 x^{n-1} +\ldots + a_{n-1}x + a_n $$ where the coefficients $a_i$ are rational numbers.
Hyperelliptic curves are so called because if you plot all the real solutions to this equation (so real values for $x$ and $y$ that satisfy this equation) they trace out a curve in the $xy$-plane. So all solutions to these equations lie on this curve. For example, the real solutions of the hyperelliptic curve $$ y^2=x^5-x $$ give the following curve:
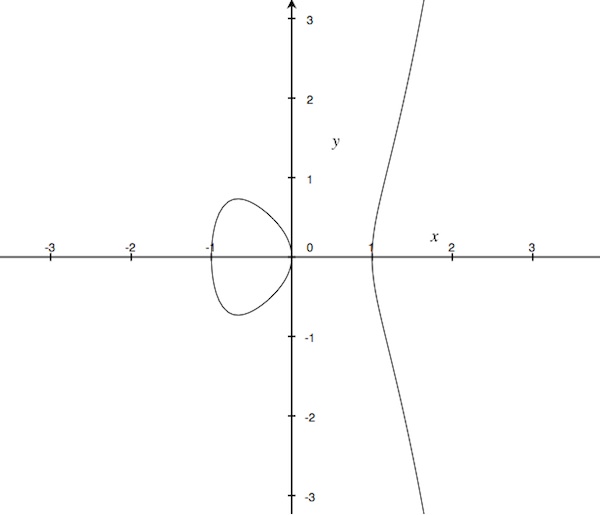
The real solutions of the hyperelliptic curve $y^2=x^5-x$"
Bhargava and his colleagues in number theory are interested in finding all the whole-number (integer) solutions of such an expression. More generally, they want to look for all the rational solutions (values for $x$ and $y$ that are both rational numbers), called the rational points on the hyperelliptic curve.
Counting donut holes
Mathematicians now regret using the terminology of curves for these mathematical objects, says Bhargava. This is because the equations defining hyperelliptic curves don't only have real solutions, they have complex solutions too. (This isn't so surprising given that complex solutions quickly fall out of more familiar quadratic equations, such as $y=x^2+1$. This has the real solutions that form the parabola you might have drawn for this equation in your maths class. But this equation also has complex solutions, such as $y=0$ and $x=i$.)
So really, to plot out all the solutions for the values for $x$ and $y$ that satisfy a hyperelliptic curve, you need to consider all complex values for $x$ and $y$, where each of $x$ and $y$ will lie on a two-dimensional complex plane with the real part of these complex values plotted against one axis and the imaginary part of the complex values plotted against the other. (You can find out more about complex numbers here.) That means that the correct place to plot out the solutions for a hyperelliptic curves is in a four-dimensional space, rather than a far more convenient two-dimensional piece of paper.
Now this four dimensional space is hard to visualise, says Bhargava. And it's also very hard to find four-dimensional graph paper! But fortunately the solutions of hyperelliptic curves are easier to visualise as they form two-dimensional surfaces, like the surface of a sphere, a donut (called a torus in maths) or the surfaces of other not too complicated objects that are essentially a sphere with some number of donut holes removed.
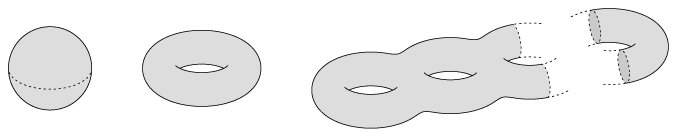
The genus of a surface is the number of donut holes that have been removed: a sphere is a surface of genus 0 and a torus has genus of 1. (Image by Daniel Müller from The Manifold Atlas Project')"
Topology is an area of maths that doesn't care if you bend or stretch things, it only cares how things are connected. The number of donut holes in a surface, called the genus of the surface, doesn't change when you bend or stretch a surface: it is a topological invariant. And the truly amazing thing, says Bhargava, is that this topological property of these surfaces is related to our original question about the rational solutions of the hyperelliptic curves that define these surfaces. (You can find out more about topology here.)
Counting solutions
Bhargava presented a result, the final part of which was proved in 1983 by Gerd Faltings, that relates the number of donut holes in a surface described by a hyperelliptic curve to the number of rational solutions satisfying the curve. If the surface has no donut holes, that is it has a genus of 0 and is essentially like a sphere, then it has either no rational solutions or infinitely many. This is a fairly useful statement, and moreover in this case mathematicians have a way of deciding whether you have no solutions or infinitely many.
The next part of the theorem, for the case when your surface has one donut hole, (that is it is essentially like a torus which has genus 1) then it has finite or infinitely many rational solutions. That's not saying much, says Bhargava.
But, the really amazing part of this theorem is for the third and final case: when you have more than one donut whole (that is, the genus is greater than 1). In this case the theorem says you have finitely many rational solutions to your hyperelliptic curve.
This theorem is truly remarkable, says Bhargava, in that it relates the genus, a topological property, to the number of the rational solutions, a number theoretic property. But the news isn't all good: although mathematicians have a way to decide the number of solutions for genus 0 curves, there is no known way to determine how many rational solutions a curve has if the surface has one or more donut holes (that is, those with genus greater than or equal to 1).
This theorem is actually true for a wider class of curves, called algebraic curves. But hyperelliptic curves have an added advantage: there is an easy way to count how many donut holes are in the surface of these curves. Mathematicians have proved that for a hyperelliptic curve of degree $n$, (that is the highest power of $x$ in the equation for the curve is $n$): $$ y^2 = f(x) = a_0x^n + a_1 x^{n-1} +…+ a_{n-1}x + a_n, $$ then the genus of the curve is the integer part of $(n-1)/2$. So for a hyperelliptic curve of degree 1 or 2, the curve has a genus of 0, and the result above says that it must have 0 or infinitely many rational solutions, and we have a way of deciding between those two possibilities. For a hyperelliptic curve of degree 3 or 4, the curve has a genus of 1, and so we have the slightly less helpful result of it having either finite or infinitely many rational solutions. And if the degree of the curve is 5 or more, the curve has a genus of at least 2, and so by the result above it has finitely many solutions.Elliptic curves – the answers on a donut
So by these results we completely understand what is going on when we have a hyperelliptic curve of degree 1 or 2. But once the degree is at least 3 we do not know how to decide how many solutions a hyperelliptic curve has. Hyperelliptic curves of degree 3 are the first interesting case, says Bhargava, as this is the smallest case where we don't know what is going on. These are called elliptic curves and you can write any such curve $E$ as $$ y^2=x^3+ax+b $$ where $a$ and $b$ are integers. And we know from the result above that the complex solutions of these types of equations trace out a torus, or donut shape, as genus of this surface is $\frac{3-1}{2}=1$ since the degree of the defining equation is 3. The real solutions of an elliptic curve form a one-dimensional curve when plotted on a flat piece of paper.
This is the first case where we don't know how to find all the rational solutions, says Bhargava. All we can say is that there are finitely or infinitely many – so not very much.
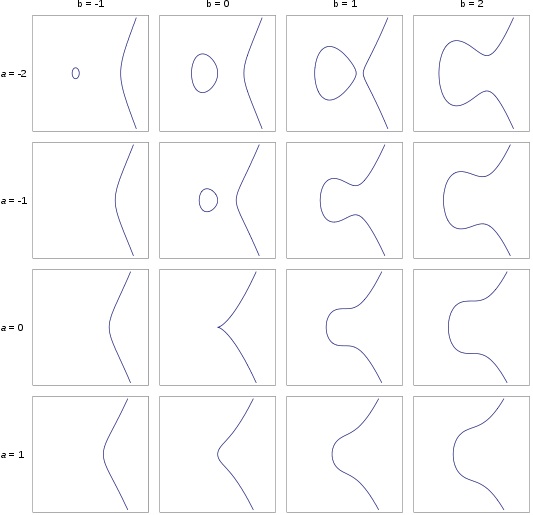
Different elliptic curves y2=x3+ax+b for different values of a and b. (Where a and b are zero the function is not smooth, so this is not actually an elliptic curve.)
Connecting the dots
What is particularly interesting about the rational solutions of elliptic curves is that they have a well understood mathematical structure: they form an abelian group. If you pick two rational solutions to an elliptic curve (two points on the elliptic curve which each have rational x and y coordinates) and you connect them with a line, then that line will intersect the curve again in at most one more point, and this point will also have rational coordinates and so be a rational solution to the elliptic curve. This means there is a way of defining an "addition" operation on the rational solutions of an elliptic curve, which acts like normal addition does on the integers. (You can read more about groups here.)
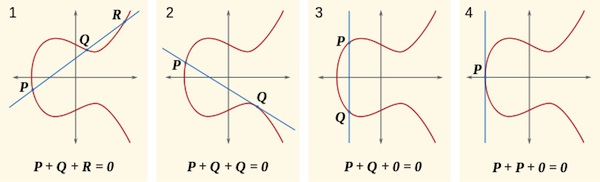
A line through two rational solutions, P and Q, on the elliptic curve will intersect the curve again in at most one point, R, which is also a rational solution. The reflection of this point in the x-axis will give the result of "addition", -R = P+Q, in the abelian group of rational solutions of the elliptic curve. If the line is tangent to the curve (say at the point Q, as in case 2, or P, as in case 4), then this is equivalent adding a point to itself (so Q+Q in 2 and P+P in 4). The only other case is that the line through P+Q does not intersect the elliptic curve (case 3) in which case we say that P+Q=0 and we say Q=-P.
With this connect the dots game, as Bhargava called it, you can define how to add two rational solutions to get a third. Moreover, thanks to a result called Mordell's Theorem, proposed by Poincaré in 1908 and solved by Mordell in 1922, you can generate all the rational solutions to an elliptic curve by playing this connect the dots game with a finite number of points. This is because the group of rational solutions to an elliptic curve is finitely generated.
The number of rational solutions you need to generate the whole group using addition is called the rank of the group. Although the set of integers, $\mathbb Z$, is infinite, it can be generated from addition starting from just the number 1: mathematicians say that $\mathbb Z$ has rank 1. If the group of rational solutions to an elliptic curve can be generated from playing connect the dots from just one solution, then it too has rank 1 and can be thought of as equivalent to the infinite set of integers. If it takes two raional solutions to generate the whole group, then it has rank 2 and is equivalent to $\mathbb{Z}^2$, all the points on the $xy$-plane that have integer coordinates – a lattice of dots drawn on a piece of graph paper where each dot is exactly 1 unit apart from the next. A rank 3 or more continues this analogy to 3, 4 and higher dimensions.
If, however, the rational solutions have rank 0, then there are only finitely many rational solutions. It's equivalent to a finite set of integers, 0 to some number $m-1$ with addition modulo $m$ (like the way you add hours on a clock face, which is addition modulo 12). It's been shown that if this is the case, there are at most 16 rational solutions. So an elliptic curve either has infinitely many rational solutions (if it is of rank 1, 2, etc) or has at most 16 rational solutions!
Average rank
So the rank of the group of rational solutions tells us a great deal about the structure of the solutions. The rank gives us a sense of how big the group of rational solutions to an elliptic curve is, says Bhargava. We'd like to know how the rank typically behaves. We have no known way of computing it for a given curve, but can we ask what we expect the rank to be if we pick some random elliptic curve?
Computing the average rank isn't entirely straightforward as there are infinitely many curves, so we need to compute the average of an infinite set of numbers. This can be done by putting the numbers in some order and then taking a limit. Bhargava uses something called the height to order the infinitely many possible elliptic curves, which is essentially a measure of the size of the curve. There are many other possible ways to measure the size of the elliptic curves, and mathematicians believe that any of these measures of size will give the same results for the average rank.
It has been conjectured (that's what mathematicians do when they're sure something is true but they haven't figured out how to prove it yet) that the average value of the rank of the elliptic curves is 1/2. In fact, the conjecture is that 50% of elliptic curves will have rank 0 (so will finitely many rational solutions) and 50% will have rank 1 (so infinitely many rational solutions, forming a group equivalent to the integers under addition). There are some curves with different ranks, such as a rank of 2, but there's so few of these that they effectively make up 0% of all possible curves so we can ignore them.
This was a bold conjecture as previously this average rank was not even known to be finite, let alone equal to 1/2, says Bhargava. He said he initially wasn't convinced that this would be true as computer experiments didn't lend much support for this conjecture. When mathematicians had calculated the average rank of millions and millions of curves up to a particular size of 108 (the size for this data was measured by something called the conductor of the curve, which is a similar measure to the height used by Bhargava in his work): rank 2 curves seem to occur more and more often the larger the curve you are looking at. In fact, says Bhargava, the computational evidence seem to suggest the least possible thing is that the average rank was 1/2!
Average way to million dollar prizes?
The first theoretical evidence for the average rank of elliptic curves being bounded came in 1992 when mathematicians showed that if the generalised Riemann Hypothesis (a generalisation of the famous Riemann Hypothesis) and the Birch and Swinnerton-Dyer Conjecture are true (almost all the mathematical community believes that they are), then the average rank of elliptic curves is bounded. "If you assume two million dollars worth of conjecture you can assume the average rank is bounded!" says Bhargava. (Both conjectures are in the list of seven Millennium Prize Problems, you can find out more here.) By the time Bhargava began to think about the question in 2003, mathematicians had managed to improve this bound through a number of results, all still conditional on the truth of the generalised Riemann Hypothesis and the Birch and Swinnerton-Dyer Conjecture: the latest result in 2007 proved that conditional to these results the average rank of an elliptic curve is bounded by 1.79.
"So this was a very exciting question for me", says Bhargava. "The data seemed to totally not support the boundedness of average rank but these important and widely believed conjectures did. It would be nice if we could prove it wasn't bounded, he says, then we would have disproved the generalised Riemann hypothesis and the Birch or the Swinnerton-Dyer conjecture!"
All of the results so far had relied on these unproved conjectures. Bhargava wanted to know if we could say something without assuming these conjectures. With colleague Arul Shankur, Bhargava managed to prove, unconditionally and not dependent on any conjectures, that the average rank of elliptic curves is less than 0.89. (You can read more here.)
By showing that the average rank was less than 1, they had shown that a positive proportion of elliptic curves had to have rank 0 (actually it is about 11%). From the results above, this means that a positive proportion of elliptic curves have finitely many rational solutions. Also, in a result with Christopher Skinner, they showed that a positive proportion of elliptic curves have rank 1, and so have infinitely many solutions. "And so, the average rank of elliptic curves being 0.5 is pretty much in the middle!" says Bhargava
In fact, rather than relying on the Birch and Swinnerton-Dyer conjecture (which previous results did), the work of Bhargava and his colleagues has provided strong evidence for this conjecture itself. Just last month in a paper with Skinner and Wei Zhang, they have been able to show that over 66% of all elliptic curves satisfy this conjecture. This is significant advancement in evidence for the conjecture as previously it had not been proved that it was satisfied by a non-zero proportion of the elliptic curves.
Although the data still doesn't seem to support the conjecture that the average rank of elliptic curves is 1/2, Bhargava's theoretical results have convinced him this is true. The problem with the data, he says, is that it is only computed for curves of a size up 108, and that's a pretty small number when compared to infinity! It may be some time before the data catches up with the theoretical results proved by Bhargava. And perhaps by the time it does he might even have proved the million dollar Birch and Swinnerton-Dyer conjecture. Given the pleasure Bhargava takes in his mathematics results, we think the money might pale in comparison to making another massive contribution to the world of mathematics.
About this article
Rachel Thomas is editor of Plus, she attended Manjul Bhargava's Fields medal lecture on 16 August 2014 at the International Congress of Mathematicians in Seoul. She would like to thank Manjul Bhargava both for his brilliant lecture and also for taking the time to talk to Plus a few days later.This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Anonymous
If both conjectures together imply the statement, then the disproval of the statement only shows that one is false.
Rachel
Thanks for spotting that - I must have misheard that sentence. It's fixed now!
Anonymous
When you wrote "that line will interest the curve again at at most one more point" you wanted to write "that line will *intersect* the curve again *in* at most one more point".
Marianne
Indeed we did! Thanks for spotting that, we have corrected it.
Anonymous
The text accompanying the figure of addition/subtraction on an elliptic curve includes the following statement: The reflection of this point in the x-axis will give defines the result of "addition", -R = P+Q, in the abelian group of rational solutions of the elliptic curve.
Either "will give" or "defines" should be omitted -- probably the former.
And, what a wonderful and approachable article. Thank you.
Marianne
Thanks for picking up the typos, we have corrected them!
Anonymous
In the section "average rank" the sentence: We have no known way to computing it for a given curve, but can we ask what we expect the rank to be if we pick some random elliptic curve? , "; "to" should be replaced with "of".
Thanks.
Anonymous
When you say "mathematicians showed that the if generalised Riemann Hypothesis" it should be "mathematicians showed that if the generalised Riemann Hypothesis".