This article is part of the Finance and physics package. Click here to see the previous article in the series.

All the chemical elements around us, except for hydrogen and helium, were "cooked" in stars like our Sun. Image courtesy .

After having explored our economic analogy for the force of electromagnetism, let us turn to the weak force. It is the force responsible for radioactive decays. For example, a free neutron (when it's outside an atomic nucleus) decays in about 15 minutes to a proton, an electron and particle called a neutrino. This is a very slow decay compared to other processes that happen on microscopic time scales. The weak force is not terribly relevant for our everyday life. However, despite its weakness, it played an important role in the history of the Universe. More specifically, in the synthesis of the chemical elements in stars. In fact, all the chemical elements around us, except for hydrogen and helium, were "cooked" in stars. The weak force played a crucial role in this process. Closer to home, we can say that the weak force can move mountains! Weak decays inside the Earth are partly responsible for maintaining its heat, which in turn moves the continents, creating the mountains.

The weak force can also be understood using a gauge theory. In this case, at each point in space we have the symmetries of a sphere, let us call it the weak sphere. See the figure below. We do not know whether the sphere is real or not. What we do know is that when we go from one point in space to another we have to rotate the sphere (just as with electromagnetism we had to rotate the circle). Knowing how to rotate the sphere requires three pieces of information, three "exchange rates": we have to specify a rotation axis (defined by two quantities) and an angle of rotation around that axis (the third quantity). Instead of carrying money, we are now carrying an object that has some orientation in the weak sphere. If we start at a country with an object in the weak sphere, as we go to the neighbouring country we have to re-orient the object according to the "weak exchange rates".

The weak force has the same symmetries as a configuration where we have a sphere at each point in spacetime. We do not know whether the circles or spheres really exist as extra dimensions. What we do know is that the gauge symmetry is the same as if they existed. The circles or spheres are useful for visualisation but we only think about their symmetry and focus only on the associated "exchange rates".

So, instead of one magnetic field, we have three different types of magnetic fields. There are equations, similar to the ones for electromagnetism, which govern the behaviour of these magnetic fields together with the corresponding electric ones.

When these equations were proposed by Chen Ning Yang and Robert L. Mills in 1954 the physicist Wolfgang Pauli strongly objected. Pauli said that the Yang-Mills theory implied that there should be new particles that don't have any mass, which are not observed in nature. This was a beautiful theory killed by an ugly fact.

Why massless particles?

To understand Pauli's objection, let us first focus on some properties of waves. In electromagnetism we have electromagnetic waves (such as light, X rays, etc). These waves have a wave length — that's the distances between successive peaks of the wave. In physical systems one is often interested in the energy needed to excite waves of various wavelengths. For a wave with a given amplitude this energy cost can depend on the wavelength. For an electromagnetic wave, the energy cost decreases when we make the wavelength longer and longer. It costs more energy to excite the wave shown on the top than it does to excite the wave shown on the bottom.

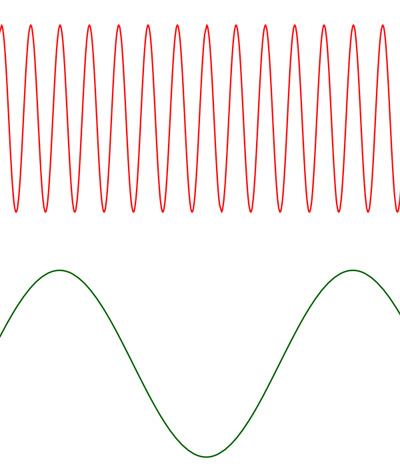
These two waves have the same amplitude, but the top one has a shorter wavelength than the bottom one. In electromagnetism it costs more to excite a wave with a shoer wavelength than it does to excite a wave with a long wavelength.

It turns out that an electromagnetic wave can also be thought of as a stream of particles (that's the famous wave particle duality of quantum mechanics — we won't go into detail, you can find out more here.) These particles are called photons. The mass of photons is related to the energy it costs to excite an electromagnetic wave with a very long wavelength. This is connected to the famous formula E = mc². Unfortunately I have not found a short way to explain this, so you will have to trust me on this.

In our economic analogy we have not talked about energy. Let us simply say that the energy increases as the gain available to speculators increases. This makes intuitive sense, the more the speculators can earn, the harder it is for the banks! Therefore configurations with less gain have a lower energy cost.

How do we represent an electromagnetic wave in our countries analogy? First notice that when you have a square of four countries, it is always possible to adjust their exchange rate so that the rates corresponding to two opposing sides of the square are 1:1. We can use our gauge symmetry to do this without changing anything. The exchange rates of the other two sides of the square simply need to be adjusted accordingly. Here is an example:

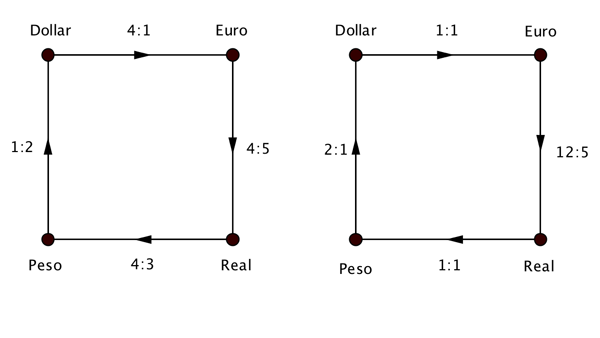
We can adjust the exchange rates so that the two horizontal edges of the square each have an exchange rate of 1:1. We need to adjust the other two exchange rates accordingly, but the overall change makes no difference.

An electromagnetic wave is represented by a whole sequence of squares as shown in the figure below, which we assume have exchange rates of 1:1 along their horizontal sides. The wave is consists of the oscillating values of the vertical sides. In each of the two example below, the amplitude of the waves, measuring the difference between its troughs and peaks, is the same. However, the top wave has a long wave length (it takes three squares to go from trough to peak) while the bottom one has a short wave length (it takes only one square to go from trough to peak).

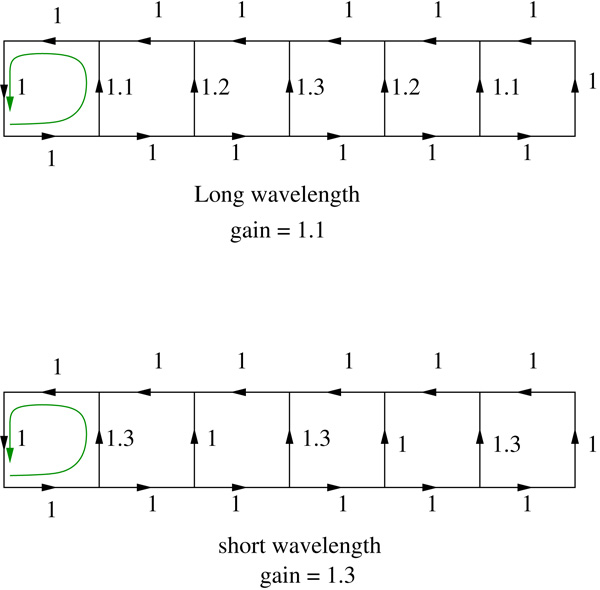
We can see two configurations of exchange rates, one with a long wavelength and one with a short wavelength. In each case the wave consists of the fact that the numbers in the middle go up and down as we move from left to right. Each segment is a bank sitting between two countries. The countries sit at the line intersections. The number indicates the exchange rate when you cross the bridge in the direction of the arrow. Notice that the total amplitude of the wave is the same; the exchange rates go between 1 and 1.3. The gain obtained by following an elementary square circle, indicated by the green lines, is smaller for the longer wavelength configuration.

You can work out for yourself that a speculator following a circuit within a single square (illustrated by the green arrow in the figure) will make a profit that depends on the difference between neighbouring exchange rates. It doesn't depend on the absolute magnitudes of the exchange rates. This is a crucial point: given a wave with a particular amplitude, a longer wavelength means smaller differences between neighbouring exchange rates (that's because the amplitude is divided into more steps). And smaller differences between neighbouring exchange rates mean less gain from following a square circuit.

We have said above that electromagnetic waves are associated to particles called photons, and that the mass of a photon is related to the energy it takes to excite a wave with a very long wave length. Using our analogy we have seen that this energy cost (the gain) goes to zero as the wavelength gets longer. This, essentially, is why the photon has no mass.

This argument works for electromagnetism and it also works for the weak force for the same basic reason. As in electromagnetism, there is a field associated to the weak force, and waves can travel through this field. These waves are related to particles, and the same argument we used for electromagnetism shows that those particles should be massless. At least it is true for the version of the weak force described so far.

Previous article: Electromagnetic economics Next article: The Higgs mechanism

Back to the Finance and physics package

These articles contribute to our Stuff happens: The physics of events project.

About the author

Juan Maldacena is the Carl Feinberg professor at the Institute for Advanced Study at Princeton, New Jersey, USA. He works on quantum field theory and quantum gravity and has proposed a connection between those two (see this article).