

One of our favourite problems from our sister site NRICH are the teacups. Imagine you have four sets of cups and saucers. One set is red, one is blue, one is green and one is yellow. In each set there are four cups and four saucers, given you a total of sixteen cups and sixteen saucers all together. This means that there are a total of sixteen different cup-and-saucer combinations, which you can arrange in a square 4x4 grid.
Here's the challenge. Can you arrange them so that:
- In any row there is only one cup of each colour
- In any row there is only one saucer of each colour;
- In any column there is only one cup of each colour
- In any column there is only one saucer of each colour
- Any cup-and-saucer combination (for example red cup, blue saucer) appears only once in the grid.
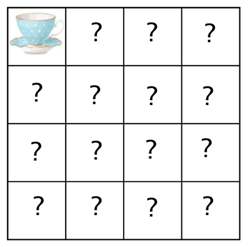
Can you arrange cups and saucers in the grid in a way that satisfies the rules? (You don't have to start with a blue cup and blue saucer in the top left corner.)
In case you haven't got four sets of cups and saucers at home, we have made these paper templates for you to cut out cups and saucers and play. Alternatively, if you can make it to this Saturday's Cambridge Science Festival Maths Public Open day there's a set of real cups and saucers for you to play with.
We love this challenge because it's a lot trickier than you might at first think. It also has an interesting history.
You may have heard about Latin squares before: they are arrangements of symbols (for example numbers) in a square grid so that every symbol occurs exactly once in every row and every column of the grid. The solution to a sudoku puzzle forms a Latin square on a 9x9 grid in which every number from 1 to 9 occurs exactly once in each row and column.
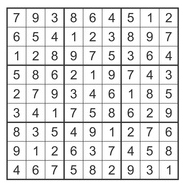
A completed sudoku grid forms a Latin square.
Our tea cups are slightly more challenging. Once you have solved the problem, the grid of cups and saucers form a Graeco-Latin square, in which there are two objects in every little square of the grid. Generally, mathematicians use symbols rather than cups and saucers when they construct such squares. For example, instead of cups and saucers you could have the numbers 1 to 4 and the letters A to D. A little square would then contain a pair made up of a letter and a number, such as A1 or D3. A Graeco-Latin square is an arrangement of symbols in a square grid, which obeys the following rules:
- Each square of the grid contains a pair of symbols, one from each of two kinds (one letter, one number).
- In every column of the grid, every symbol occurs exactly once. And the same is true for each row. (Each number, and each letter, exactly once in every column and every row).
- Every possible pair of objects occurs exactly once in the entire grid.
Graeco-Latin squares were studied extensively by Leonhard Euler, one of the most prolific mathematicians of all time, at the end of the 18th century. Euler was inspired by a puzzle called the 36 officers problem. Imagine there's a war and you're in command of an army that consists of six regiments, each containing six officers of six different ranks. Can you arrange the officers in a 6x6 grid so that each row and each column of the square holds only one officer from each regiment and only one officer from each rank? In this case, the two "symbols" in each little square are the rank and regiment of an officer. The difference to the teacup puzzle is that here we are dealing with a 6x6 grid, rather than a 4x4 grid.
Euler gave a lot of thought to the 36 officers problem, and eventually concluded that, "We have to admit that such an arrangement is impossible, though we can't give a rigorous demonstration of this". A proof that the problem is impossible to solve didn't come along until nearly 130 years later, when the French mathematician Gaston Terry provided it in 1901.
So what about our teacup puzzle? As you may already have found out, a solution does exist in this case. It would be cruel to present you with an unsolvable problem! In fact, there are a total of 1152 solutions. Once you have found one solution, you can immediately generate others: simply rotate or reflect the arrangement and the result is also a solution.
These solutions (involving only the saucers, so they form a Latin square — we don't want to give the whole solution away) look different, but they are related through rotations: rotate the first solution by 90 degrees clockwise and you get the second (top right), another 90 degree rotation gives the third solution (bottom left), and another gives the fourth (bottom right).
If you consider solutions related by such symmetries to be the same, because essentially they are, then the number of solutions shrinks to 144. The idea that problems and their solutions can exhibit symmetries is an important one in mathematics and theoretical physics, and often provides a powerful tool, not only to solve problems, but also to sniff out new lines of inquiry.
What if we are dealing with five sets of cups and saucers, or six, seven, or any other positive number? In that case we would be looking for a 5x5, 6x6, 7x7, or, more generally, an nxn Graeco-Latin square. Euler showed that nxn Graeco-Latin squares exist for all odd numbers n and for all numbers n that are divisible by 4. The number n=6 doesn't belong to either of these classes, and as we have seen with the 36 officer problem above, a 6x6 Graeco-Latin square doesn't exist. Euler believed that the same was true for any even number n that is not divisible by 4. In other words, that there is no nxn Graeco-Latin square for n=6, n=10, n=14, etc. So did many other people, until Euler was proved wrong in 1960. The mathematicians Raj Chandra Bose, Sharadchandra Shankar Shrikhande and E. T. Parker enlisted the help of computers to prove that Graeco-Latin squares exist for all n except 2 and 6.
But Euler's work on Graeco-Latin squares wasn't a failure. As one would expect from a great mathematician, he persevered, and even though his initial conclusion was wrong, he came up with interesting and important new ideas in the process of tackling the problem. The 36 officer problem inspired Euler to contribute important work to an area of maths called combinatorics which, as you may have guessed, is about combining objects in ways that satisfy particular constraints. It has many applications in the real world - from designing schedules, such as school timetables or sports tournaments, to detecting patterns, for example in DNA sequences or large amounts of data.