
This article is part of our package on the maths of materials, which is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below.
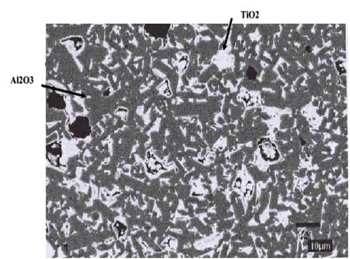
A mixture of aluminium oxide and titanium oxide.
Suppose that you want to construct a building at an airport. If that building reflects radar waves then you have a problem. The radar at the airport, or from the aircraft landing or taking off there, will reflect off the building at all sorts of angles. The result is that the radar system gets confused and the radar displays get cluttered. Therefore it is a good idea to cover buildings with a material that absorbs the radar waves. The same principle applies if you want to make a stealth aircraft invisible to radar (rather like Harry Potter's invisibility cloak). During the Second World War it turned out that nature had already solved this problem. The famous de Havilland Mosquito was made of wood, and this made it almost invisible to the German radar systems.
Now, the challenge is to make a synthetic material with the same radar absorbing properties. To do this we make use of the new ideas of complexity and of emergent properties. Loosely speaking, a complex material is something which is made up of many different materials. An example is carbon fibre, which is used in many different applications, from aircraft engines to fishing rods. The key feature of such a complex material is that its properties are much more than the sum of the different component properties. Instead they reflect the way that these different properties interact. Or more poetically, the whole is greater than the sum of the parts. Such properties are then said to emerge from the interactions, and may be very different from the original properties of the component materials. The only way to find out what these emergent properties are is to use quite sophisticated mathematics.
The question of designing such a radar absorbing material came to our team at the University of Bath, and it was decided to make a complex meta-material combining the different electrical properties of aluminium oxide and titanium oxide. On the technical side, one of these behaves like a resistor, and the other like a capacitor. Resistors have electrical properties that are independent of the frequency of the electrical waves that pass through them. In contrast, capacitors conduct electricity well at high frequencies, and badly at low frequencies.
To create the complex material we took a random mixture of these two different materials mixed in careful proportion. You can see a picture of the resulting mixture above. As you can see it is very complex, and hard to analyse, even using the multi-scale methods described in Crystal clear. Instead we use a branch of mathematics called random matrix theory to study them.
The material above can be modelled by a network of resistors and capacitors, see below.
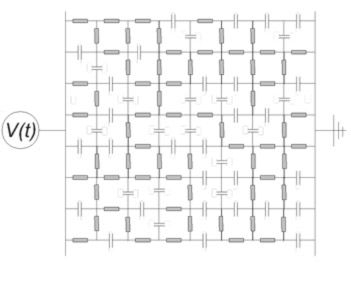
A network of resistors and capacitors.
Now we use a trick often employed in studying complex problems. Instead of trying to exactly reproduce the parts of the material we instead consider them to be randomly placed according to certain statistical rules. We then look at the statistics of the electrical properties of the resulting network, in particular its conductivity. The network of resistors and capacitors itself can be represented by a matrix (an array) with random entries, and its statistical properties found by the theory of such random matrices. This turns out to be a very powerful technique for predicting the properties of the original material and gives excellent results. (We use the same idea of representing complex processes by random variables in many other applications, including studies of the behaviour of the stock market and the movement of crowds of people.)
Below you can see the result of our efforts. On the right is the conductivity of the material as a function of frequency, and on the left the paths of the current through the network at the frequency indicated by the arrow.
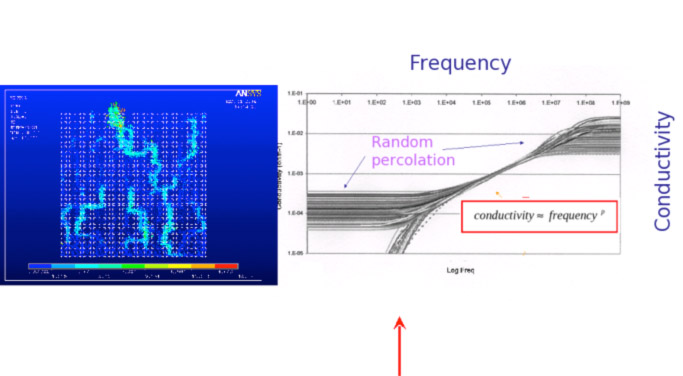
These results agree very well with experiment. Random matrix methods are now finding many other applications to the design of many other complex materials.
About this article
This article is based on a talk in Budd's ongoing Gresham College lecture series. A video of the talk is below.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.