Crystal clear

This article is part of our package on the maths of materials, which is based on a talk in Chris Budd's ongoing Gresham College lecture series. You can see a video of the talk below.

Let there be light: Photonic crystals

A cross section of a photonic crystal.

Crystals are fascinating for their beauty and regular structures, but they are also useful in communication. Early in the twentieth century it was discovered that crystals could be used in radios, both to detect signals imposed on radio waves (in the celebrated crystal radio sets which I used to build) and then to fix the frequency of the same waves. The same technology is used in digital watches to give a highly accurate time piece.

More recently crystals, as well as glass, have been used in fibre optic technology. If you have broadband, the broadband signal is likely to be transmitted along a fibre-optic cable, at least for some of its path. It is a simple fact that light going down such a cable can not only convey much more information than going through a wire, but can also be transmitted without a lot of loss of signal. This observation led the designers of fibre-optic cables to think about whether it is possible to reduce the attenuation (that is, the loss) of the signal still further. This would allow very long distance communication without the need for any units to boost the power. It's especially important for the transmission of signals under the ocean.

The question has been answered with the use of some very fancy mathematics relating to so-called photonic crystals. An example of such a crystal is shown above. As you can see it is made up of a fibre optic cable with a regular lattice of holes drilled into it. Photonic crystals aren't easily found in nature. Instead, they are a so-called meta material, designed to have specific properties.

To study such crystals we set up the (partial differential) equations for laser light moving through glass. There are a number of such equations, including the Helmholtz equation and the nonlinear Schrödinger equation, for example. The precise equation used depends upon the intensity of the laser light beam, and also the type of crystal used. The Helmholtz equation is the simplest of these: if $u$ is the intensity of the laser light, then it satisfies the partial differential equation

$\frac{\partial ^2 u}{\partial x^2}+\frac{\partial ^2 u}{\partial y^2}+\frac{\partial ^2 u}{\partial z^2}+ \omega ^2 u(x,y,z)=0,$

where $\omega$ is the frequency of the light wave and $x$ , $y$ and $z$ are the three spatial coordinates.

To solve this equation for $u$ you need to stipulate boundary conditions, and these encode the geometry of the photonic crystal. The solution then shows that at certain frequencies the holes in the crystal act as miniature resonant cavities whose walls reflect the light back and forth. These resonant cavities effectively stop the light beam going through the middle of the crystal from leaking out through the sides.

The effect is an effectively loss free cable, provided that it can be manufactured in the first place. Fortunately this is now possible. The picture above shows an example of just such a photonic crystal. As you can see it is a very complex shape. Until fairly recently it was thought impossible to analyse the behaviour of light in such a crystal without the use of huge, and expensive, computing power. However advances in manufacturing have gone hand in hand with advances in mathematics. Indeed it is because of the development of new mathematical techniques that we are not only able to analyses these complex shapes, but also to predict their optical performance with some precision.

The new mathematical techniques are called multi-scale homogenisation methods and they work by recognising that in a material such as a photonic crystal several different length scales are important. First, there is a micro scale given by the wavelength of light. Then there is an intermediate meso scale given by the size of the holes of the crystal. And finally, there is a macro scale given by the width of the whole crystal. (Many other materials have several scales, two natural examples are wood, bone and cells). The material behaves differently at these different scales, and its properties result from the way in which these different behaviours interact. Multi-scale mathematical methods allow us to understand this behaviour and thus predict the behaviour of photonic crystals without the need of a super computer. Multi-scale methods now have many more applications, ranging from weather forecasting to structural optimisation.

Going liquid

At school we are told that materials are either liquids, solids or gases. This is not strictly true. Depending on the arrangement of their molecules materials can be in an intermediate state between being a solid and a liquid. An important example of such an intermediate state are liquid crystals. These materials play a vital role in modern technology.

The arrangements of molecules for a crystal in the nematic phase, which is between solid and liquid. Image Kebes, CC BY-SA 3.0.

The key feature of a liquid crystal is that its molecules are long and thin, so they come with a direction. Such materials are called anisotropic and are very different from isotropic liquids which have no preferred direction. The properties of anisotropic crystals can all be determined by mathematical arguments. In the figure on the left you can see the arrangements of molecules for a crystal in the nematic phase, which is between solid and liquid.

What makes nematic liquid crystals useful in technology is that the direction of the molecules can be changed by an electrical or a magnetic field, and this change can alter the crystal's conductivity, viscosity, compressibility and, crucially, its refractive index, which describes how light propagates through the crystal. Their response to light gives liquid crystals many applications in liquid crystal displays (LCDs) which can be found in computer screens and nearly every other type of display medium. (Possibly the first example of LEDs were the screens used in early digital watches.) Nematic liquid crystals are also used in optical switches, sensors and elastomers (a visco-elastic polymer).

Mathematics is hugely important in the design of LCD devices. In particular in the recent development of bi-stable displays which require no energy to display information, only to change it. The mathematical approach to such a design is to find a formula describing the energy of the liquid crystal state and then proving rigorously that this energetic state has two stable configurations. This takes us back into the realm of partial differential equations, which we will also meet in the next section.

Crystals and separating phases

Crystals themselves have a strong link to mathematics: their shape, their symmetries, their size and their strength can be understood using mathematical methods. A recent example of the relevant of maths to crystals is the celebrated Bucky ball; a form of carbon, in which 60 carbon atoms are arranged geometrically in the shape of a soccer ball made of twenty hexagons and twelve pentagons. It is shown below.

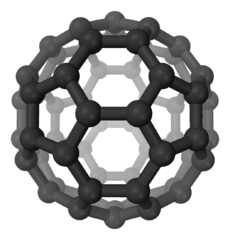
A Bucky ball.

Mathematicians call this shape a truncated icosahedron. Crystals take such symmetric shapes, not because these shapes are particularly beautiful (although of course they are), but because they represent so-called minimal energy states for the molecules. Any material, when left alone, will naturally assume such a state, which out of all states the material could be in requires the minimal amount of energy to maintain. Minimal energy states make the crystals both strong and stable.

Understanding energy turns out to be the key to understanding many different types of material, including the liquid crystals that we looked at in the previous section. To do this mathematically you need to find a formula for the energy of the crystal and then find the configurations of the material's molecules that minimise this energy. This simple idea is the key behind unlocking the secrets of many materials and allows us to predict many varied and exotic shapes of those materials.

Computer simulation of the two phases in a two-phase material. Image courtesy National Institute of Standards and Technology.

One example of this is a two-phase material, consisting of distinct parts with different chemical or physical properties, such as a cooling metal that is solid is some areas and liquid in others. Such a metal can form exotic patterns like the one illustrated on the right, in which the distinct parts of the material are represented by different colours. It is possible to describe, understand, predict, classify and control these patterns.

One model for pattern formation in a two-phase material is the celebrated Cahn-Hilliard equation:

$\frac{\partial c}{\partial t} = D\nabla ^2 \left(c^3-c-\gamma \nabla ^2 c\right).$

In this partial differential equation $c$ takes the values of $+1$ in one of the phases and $-1$ in the other. Here $D$ is a constant that measures how the liquid diffuses, $\gamma$ is a constant related to the energy of solidification, and $\nabla ^2$ stands for

$\nabla ^2=\frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}.$

The expression describes how the phases evolve in time and in space to give the shapes above. The Cahn–Hilliard equation has applications in polymer science, complex fluids and many other industrial applications and is a major tool in allowing mathematicians to predict the behaviour and form of complex materials which are binary mixtures of two other materials.

About this article

This article is based on a talk in Budd's ongoing Gresham College lecture series. A video of the talk is below.

Chris Budd.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.