In 2018 The Guardian ran the relationship project, a "state of the nation report on Brits inlove". The project was run in partnership with TSB with the research being done by Ipsos MORI.
In one of the project's [ https://www.theguardian.com/the-relationship-project/2018/feb/21/how-many-break-ups-does-it-take-to-find-the-one ] articles we came across the following sentence:
"The average Brit will have had three long-term romantic relationships in their lifetime, instigating 2.29 break-ups themselves."

Not all relationships last forever, but the numbers need to balance.
This, we thought, seems mathematically impossible. For every person who is instigating a break-up there's a person who is being broken up with, so the numbers should balance with every Brit instigating, on average, 1.5 break-ups.
It's actually not too hard to prove this. Imagine a population of $N$ people in which there have been $x$ long-term relationships in total. This means that on $x$ occasions someone has done the breaking up and someone has been broken up with. The average number of times a person instigates a break-up is therefore $x/N$ and equals the average number of times a person has been broken up with. Adding those two together gives the average number of relationships per person, regardless of who did the breaking up: $2x/N$. Since $2x/N=3$ it follows that $x/N$, the average number of times a person instigates a break-up, is 1.5. This calculation assumes that all the relationships have finished, which of course isn't the case in reality. However, the average number of \emph{finished} relationships per person is less than or equal to the average number of relationships per person. So if we take account of the fact that some relationships might still be going on, but still write $x$ for the number of finished relationships, we get that $2x/N \leq 3$, which means that $x \leq 1.5.$ It definitely can't be 2.29.So what is behind the Guardian's statement? One possibility is that it was clumsily phrased, and that the figure of 2.29 was calculated with all broken-up relationships in mind, not just the long-term ones. Indeed, in other articles belonging to the relationship project the figure is quoted without any reference to long-termism. If that is the case, then all is well mathematically, and the problem down to fuzzy writing.
We couldn't resist, however, to see if there are other explanations. For example, could it be that the statement refers, not to the mean average, but to the median? The mean average of a list of numbers is the sum of the numbers divided by how many numbers there are in total. It's the kind of average we considered above. To get the median, you list all your values in numerical order, including repeated ones, and find the number that's right in the middle of your list (if there isn't a middle because there are an even number of values, then the median is the value that lies half-way between the two middle values). Thus, the median of the list 1, 2, 3, 4, 5 is 3, and the median of the list 1, 2, 3, 4 is 2.5.
The median is often used to define the average person with respect to some activity or characteristic, such as long-term relationships: of you lined all Brits up in order of how many long-term relationships they have had, the median would be marked by the person right in the middle, which is a good reason for calling them an average person. The mean, on the other hand, tells us how many long-term relationships there would be per person if the relationships were distributed evenly in the population.
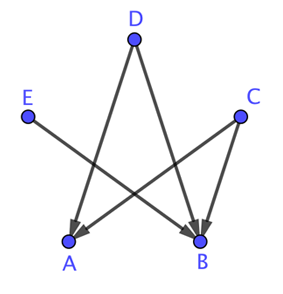
Relationships between a population of five people. An arrow between two nodes means that they two corresponding people have had a relationship. The direction of the arrow indicates who broke up with whom: an arrow pointing from node x to a node y means that node x ended the relationship. The median number of relationships is 2, the median number of break-ups instigated is 1, and the median number of break-ups "received" is 0.
In theory, it is perfectly possible for the median number of instigated break-ups and the median number of break-ups "received" to not be equal, and to not add up to the median number of long-term relationships. We have created a toy example where this is the case (see left). However, the number of break-ups instigated by a person is a whole number (we assume). A median that lies between two and three means that half the population instigated at most two break-ups and the other half at least three. The median should therefore be 2.5. Quoting it as 2.29 is non-sensical (and technically wrong).
Without more detail about the survey and how it was analysed, it's hard to tell what exactly is going on here. If we are talking means, then the discrepancy could in theory be down to a bias in the sample of people who took part in the survey. In our calculation above we assumed a closed population, that is, a population in which individuals only have relationships with individuals who are also part of the population. While the entire population of British adults is probably more or less closed in that sense, a smaller sample (1,932 British adults aged 18+ for this study) obviously isn't. In this case more break-ups could have been instigated by people in the survey than received by people in the survey, with the "missing" received break-ups involving people outside the survey. However, the whole point of choosing a large, and random, sample is to avoid such accidental biases.
In theory the discrepancy could also be down to subjectivity. Few break-ups are clear cut, and there must be situations in which both ex partners think that they ended the relationship. This would inflate the average number of break-ups instigated per person, and could thus explain the statement. It would perhaps also tell us something interesting about how people break up and what they feel about it.
Perhaps a future Guardian article will shed some light on the issue. The whole thing reminds us of the third National Survey of Sexual Attitudes and Lifestyles in which men reported having had twice as many sexual partners, on average, than women. In a closed population with roughly as many males as females (which there are) this is also mathematically impossible (see here for a proof). In this case, the results of the survey are clearly presented and we know that the average is the mean average. Scientists are still arguing how the discrepancy might arise. Explanations range from men inflating their numbers and women deflating them, men and women differing as to what constitutes a sexual partner, and men's visits to prostitutes (who were not part of the survey) skewing the numbers. You can find more about this, and other, statistics about our sex lives in David Spiegelhalter's excellent book Sex by numbers.