Add new comment

Maths around the clock

On clock dials you find the numbers from 1 to 12 — but for a bit of a change, could you write those numbers in a different way?

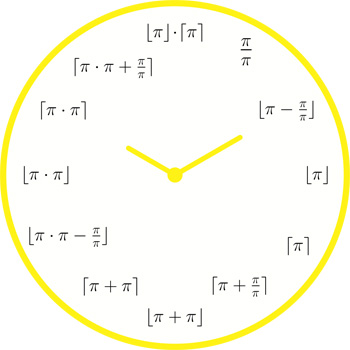
A π clock. See below for more examples.

The answer is yes. For example, you can write $4$ as $2+2$ or $2\times 2$ or $2^2$ by using the sum, the product, or by raising to a power. If you like the number $\pi$ you could also write $4$ as $\lceil \pi \rceil$ by using the ceiling function, which approximates $\pi$ from above with the closest integer. There are infinitely many possibilities for expressing the number $4$ , and which one is the best is a matter of personal preference. In general, you can produce your own exclusive mathematical clock by writing $1$ to $12$ in your favourite way.

If you are looking for something extremely fancy, you can use Euler's identity to express $1$ using the numbers $e$ , $\pi$ , and the imaginary number $i$ :

$1=-e^{\pi i}\, .$

Or, if you like the Basel problem you could display $6$ as the inverse of the sum of all reciprocals of the squares of the positive multiples of $\pi :$

$1/6=\frac{1}{(\pi )^2}+\frac{1}{(2\pi )^2}+\frac{1}{(3\pi )^2}+\frac{1}{(4\pi )^2}+\frac{1}{(5\pi )^2}+\ldots$

For something more concrete, you can pick any digit from $1$ to $9$ and express the numbers on the clock dial only with this digit and mathematical symbols (some examples are provided in the images below).

Much more generally, it is possible to write the integers from $1$ to $12$ by using only any given real number and mathematical symbols. The reason is that we can always find a suitable expression for the number $1$ . Indeed, for a positive real number which is at most $1$ , it suffices to take the ceiling function (ie taking the integer approximation from above) to produce $1$ . For any real number $x$ greater than $1$ we can write $1$ as the floor function of $\sqrt[x]{x}$ (ie taking the integer approximation from below of the $x$ -th root of the number $x$ ), as can be checked with the logarithmic identity

$\sqrt[x]{x}=e^{\frac{\log x}{x}}\, .$

Finally, negative numbers may be turned positive with the absolute value, and for $0$ one may use the factorial identity $0!=1$ .

There are plenty of mathematical clocks in circulation with various expressions on the clock dial. Occasionally, rather than having the numbers from $1$ to $12$ , you find the first twelve terms of some sequence. For example, you may have the first twelve Fibonacci numbers:

$1,1,2,3,5,8,13,21,34,55,89,144\, .$

In the very same way, you could use the letters from $A$ to $L$ .

Another option is writing down an equation such that the desired number is the only solution, for example conveying $5$ with

$x^2+7=10x-18\, .$

Some mathematical clocks show equations with more than one solution, but with exactly one solution among the integers from $1$ to $12$ . In general, beware of mathematical inaccuracies in mathematical clocks (for example $3$ is not really $\pi -0.14$ )!

Nevertheless, everything is allowed to have fun playing with numbers. We challenge you to produce your own mathematical clock, but if you need some inspiration here are some examples.

Mathematical Clock Themes

In the image gallery below you find various mathematical clocks, with alternative ways of writing the numbers from $1$ to $12$ . You can print out one of those images and use it as a clock dial (e.g. you buy a clock with a custom dial), or you can simply place selected numbers' expressions above or around your clock. You can also buy clocks that you can write on, which allow you to change your mathematical clock at leisure.

Here are some examples:

1 to 9 clocks

Fix any decimal digit from $1$ to $9$ and then display all integers $1$ to $12$ with short expressions involving only that digit and some arithmetic operations. We use the basic arithmetic operations, taking powers, and taking the square-root.

Here is an example of a 7 clock. Examples for 1, 2, 3, 4, 5, 6, 8, and 9 are given below (notice that with the digits 5, 6, and 7 we only use the basic arithmetic operations).

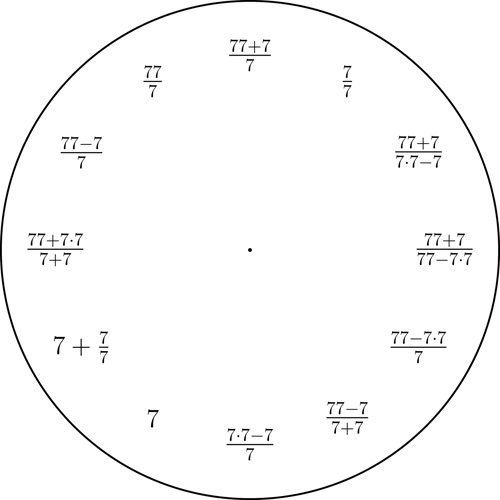
A 7 clock. Click here for a printable pdf of this clock face.

The 123 theme

It is possible to write all integers from $1$ to $12$ using only the digits $1$ , $2$ , $3$ exactly once and in this order. We use the basic arithmetic operations, taking powers, taking the square-root, taking the factorial (the factorial of a natural number $n$ , denoted by $n!$ , is defined as the product of all natural numbers from $1$ to $n$ ), and applying the floor function $\lfloor \, \rfloor$ (this function approximates a real number with the closest integer from below).

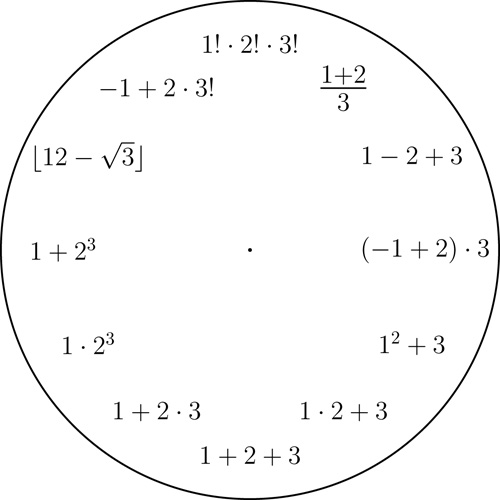
A 123 clock. Click here for a printable pdf of this clock face.

The π clock

It is possible to write all integers from $1$ to $12$ using only the number $\pi$ , the basic arithmetic operations, and the floor/ceiling functions $\lfloor \, \rfloor$ and $\lceil \, \rceil$ (these functions approximate a real number with the closest integer from below and above, respectively).

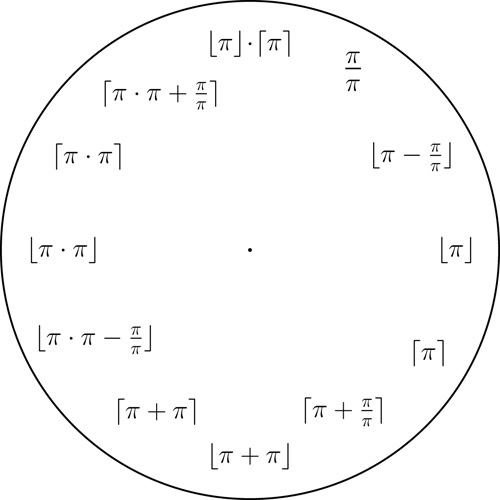
A pi clock. Click here for a printable pdf of this clock face.

The e clock

It is possible to write all integers from $1$ to $12$ using only Euler's number $e$ , the basic arithmetic operations, taking powers, taking the square-root, and applying the floor/ceiling functions $\lfloor \, \rfloor$ and $\lceil \, \rceil$ .

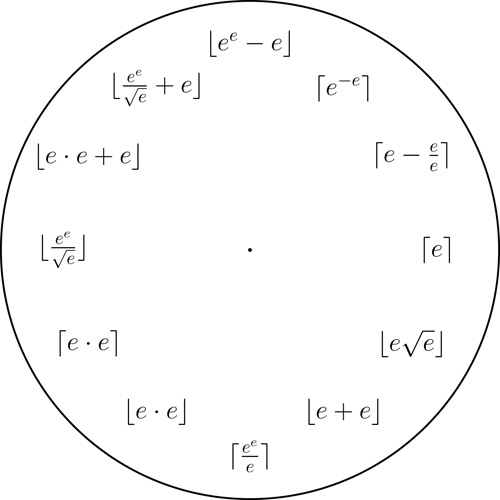
An e clock. Click here for a printable pdf of this clock face.

The binary clock

Here we write all numbers from $1$ to $12$ in the binary system, which only uses the digits $0$ and $1$ .

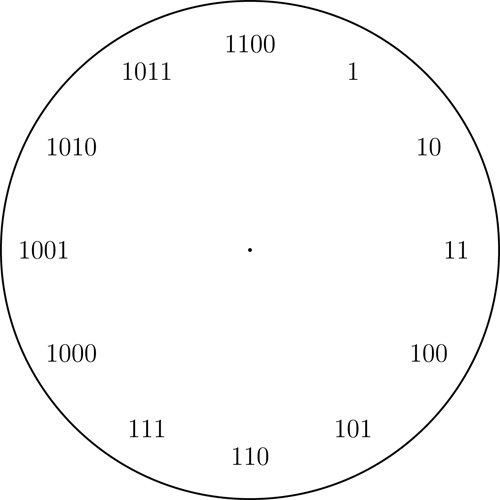
An binary clock. Click here for a printable pdf of this clock face.

The prime numbers clock

Here we only write those numbers from $1$ to $12$ which are prime numbers.

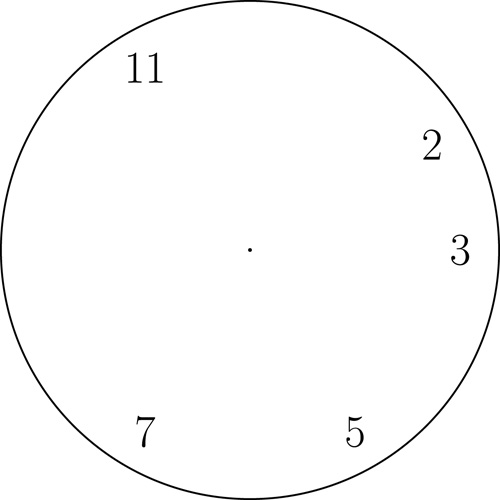
A prime number clock. Click here for a printable pdf of this clock face.

The Chinese numerals clock

Here we write all numbers from $1$ to $12$ using Chinese numerals: you may notice how the numbers $11$ and $12$ are composed from the symbol for $10$ and the numbers $1$ and $2$ respectively.

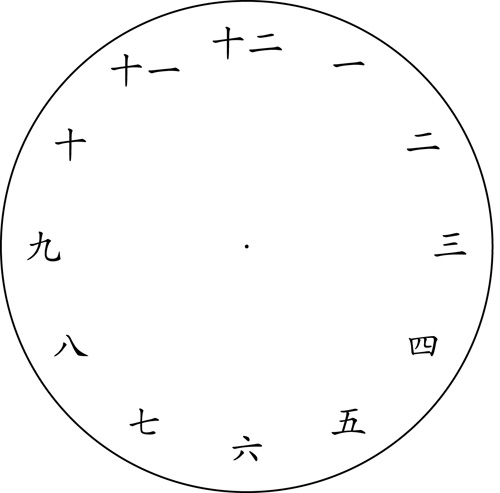
A Chinese numerals clock. Click here for a printable pdf of this clock face.

The Maya numerals clock

Here we write all numbers from $1$ to $12$ using Maya numerals: a dot stands for the number $1$ and a bar stands for $5$ .

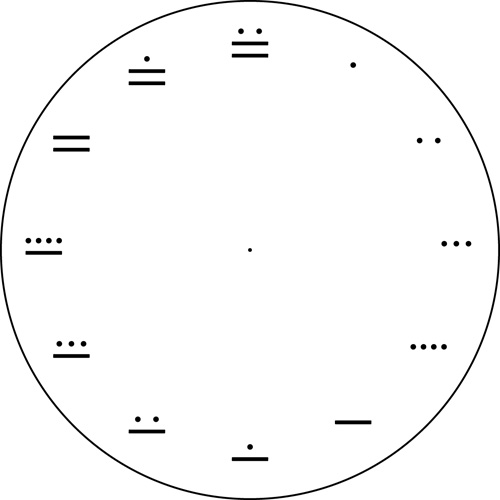
A Maya numerals clock. Click here for a printable pdf of this clock face.

The $\pi$ clock, the $e$ clock, the $1$ to $9$ clocks and the $123$ clock were developed by the author (for the $123$ theme, we got some inspiration from Math clocks).

More examples...

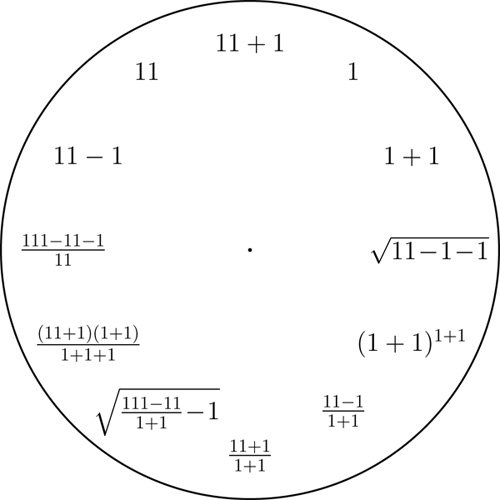
A 1 clock. Click here for a printable pdf of this clock face.

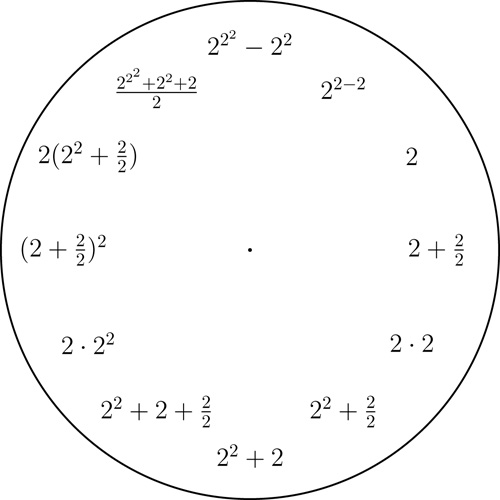
A 2 clock. Click here for a printable pdf of this clock face.

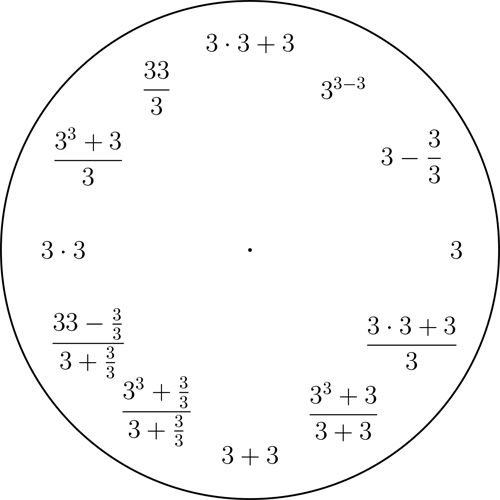
A 3 clock. Click here for a printable pdf of this clock face.

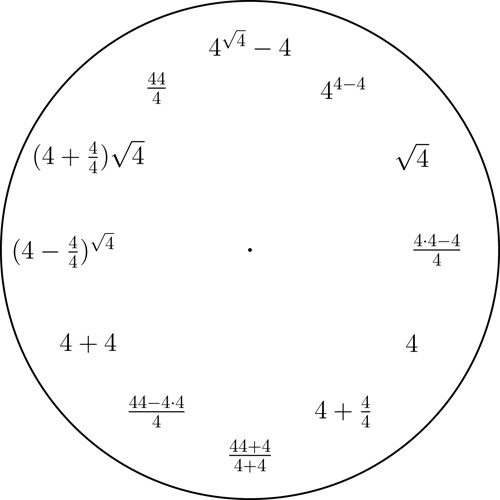
A 4 clock. Click here for a printable pdf of this clock face.

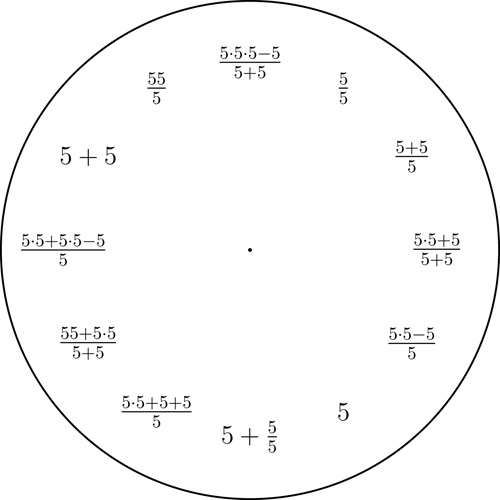
A 5 clock. Click here for a printable pdf of this clock face.

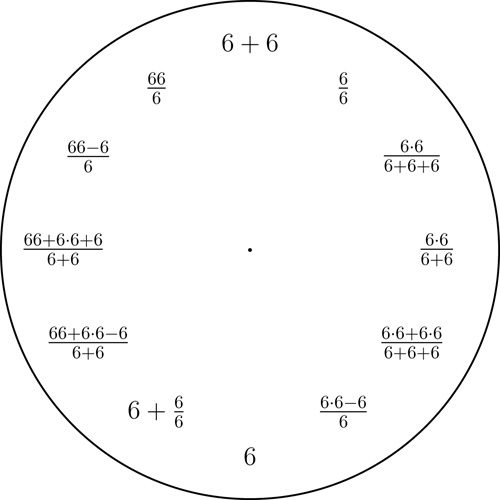
A 6 clock. Click here for a printable pdf of this clock face.

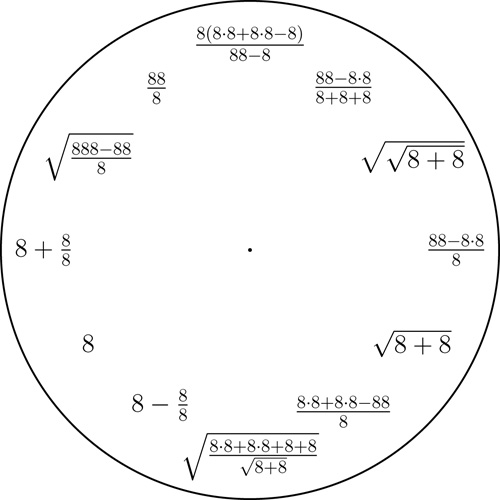
A 8 clock. Click here for a printable pdf of this clock face.

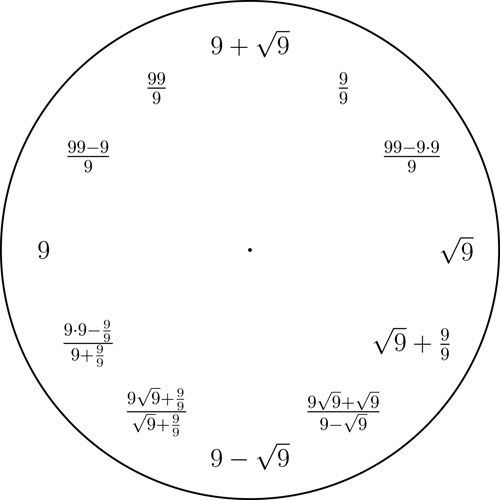
A 9 clock. Click here for a printable pdf of this clock face.

About the author

Antonella Perucca is Professor for Mathematics and its Didactics at the University of Luxembourg. She is a researcher in number theory and invents mathematical exhibits (for example the "Chinese Remainder Clock"). To find out more, explore her webpage.

Plus.Maths.org