
On the seventh day of advent we venture to a dark place we will never return from.

Simulated view of a black hole. Image: Alain Riazuelo.
A black hole is a region of spacetime where the force of gravity is so strong that nothing, not even light, can escape from the region. Black holes are formed when a lot of mass is concentrated in a tiny region of space. For example, if we managed to concentrate all the mass of the Earth into a sphere of a radius of a few centimetres, then that object would be a black hole. That's because densely packed mass exerts an immense gravitational pull. You can easily see this by considering Newton's law of gravitation.
Suppose you are sitting on the surface of an extremely dense spherical body with a very large mass $M$ and a very small radius $r$. The gravitational force holding you to the body's surface, according to Newton, has magnitude $$F= G\frac{M m}{r^2},$$ where $m$ is your own mass. Now since $M$ is very large and $r$ is very small, $F$ in turn is very large. The body exerts a huge gravitational pull, and to escape its clutches you'd need to accelerate away from it very hard indeed.That makes sense, but it turns out that Newton's theory of gravity is out-dated. It still works on the scales we deal with in everyday life, but when it comes to astronomical scales, we should really think in terms of Einstein's theory of general relativity. The concept of black holes exists here too. General relativity predicts that massive objects, such as planets and stars, can warp the very fabric of space and time (see door #2 of the advent calendar). The warping of spacetime changes the trajectory of objects that are less massive than the body that causes the warping: they move towards the massive body or orbit around it: that's what we interpret as the force of gravity.
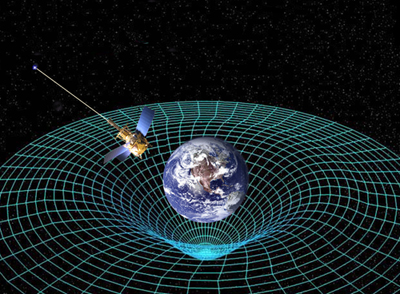
Massive bodies warp spacetime. Image courtesy NASA.
A black hole is a region of spacetime that is extremely warped. If the theory is to be believed, then the curvature of spacetime is infinite within a black hole (the black hole contains a singularity). But we don't know whether this is really true for black holes that exist in nature: it might just be an artefact of the theory. In any case, gravity is so strong within a black hole that not even light can escape.
But Einstein's theory also says that nothing can travel faster than light. This includes information, because information must always be conveyed via some physical signal, such as sound or light. Since light cannot escape from a black hole, neither can information: whatever happens in a black hole cannot be communicated to the outside world.
A black hole comes with a boundary of no return, called its event horizon. Once you have passed that horizon, you will never ever come back. But what will happen to you? If the black hole is small then the difference between the curvature of spacetime at your head and at your feet is so large that you get stretched, like spaghetti. But if the black hole is very big then the gravitational field is very uniform, even though it's strong, so the difference between gravity at your head and at your feet wouldn't be that large. You can approach the horizon of a very big black hole, such as the one at the centre of a galaxy, and not feel anything at all.
Close to the black hole, because gravity is strong, time runs slower for you. Even if you could stay there you wouldn't feel much, but if you compared your clock with the clock of an observer far from the black hole then you would see that you haven't aged that much whilst he or she has become much older. Other than that you'd be perfectly fine at first. However, general relativity tells us that once you are inside the black hole you will eventually hit the singularity at its centre and you will be destroyed.To find out more about black holes see upcoming doors of our advent calendar.
This year's advent calendar was inspired by our work on the documentary series, Universe Unravelled, which explores the work done by researchers at the Stephen Hawking Centre for Theoretical Cosmology and is available on discovery+. Return to the 2020 Plus Advent Calendar.