
Over the last year and a half we have all become used to the term exponential growth. Mathematically, the nature of this kind of growth is captured by the expression
$$e^x,$$ where $e=2.71828...$ is a mathematical constant called Euler's number (see here to find out why). The expression grows incredibly quickly as $x$ grows larger. When we are looking at a negative exponent, so we have $$e^{-x},$$ where $x$ is positive, then the expression becomes smaller incredibly quickly as $x$ gets larger. You can see that in the graphs below.
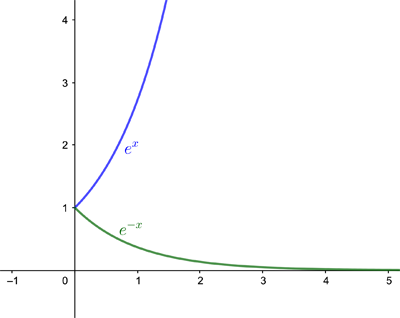
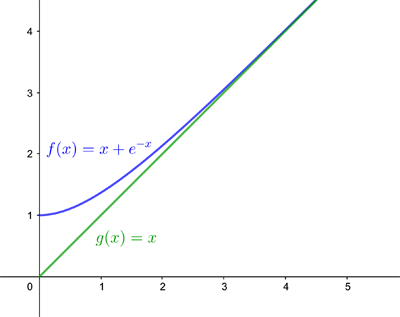
\emph{Exponentially small terms} are expressions of the form $e^{-x}$ where $x$ is positive and very large. Because such terms are very small, these are often ignored when they turn up in mathematical expressions. For example, the function $$f(x)=x+e^{-x}$$ looks very much like $$g(x)=x$$
for large positive $x.$ If you're only really interested in what happens to $f(x)$ when $x$ is large, you might as well ignore the exponentially small term and just look the simpler function $g(x)$ instead. Mathematicians say that the function $g(x)$ is a good \emph{asymptotic approximation} for $f(x).$ Loosely speaking, an asymptotic approximation of a function of a variable $x$ is one that works when $x$ is large in magnitude. (See here to find out more about asymptotes.)
The example above was simple enough, but it turns out that in more complicated situations ignoring small exponential terms can be dangerous. "[The terms] may be exponentially small in one region [but as your variable changes] they can grow and come to dominate your mathematical solution in the end," says Chris Howls of the University of Southampton and an expert in the field.
Since asymptotic approximation is used a lot by applied mathematicians, who might for example be modelling the jet engines of the planes we travel in, it's important to keep on top of such potentially explosive exponential terms. That's the purpose of a research programme that Howls helped to organise at the Isaac Newton Institute for Mathematical Sciences in Cambridge this year, which is due to continue next year. It's called Applicable resurgent asymptotics.
Rebellious maths
One way in which exponential terms can pose a danger was first discovered by the mathematician George Gabriel Stokes in 1850, when he was investigating a question about rainbows first raised by George Biddell Airy.
The functions Stokes was considering did not, as in our example above, take real numbers and input. Instead, they took points of the plane as input, allocating to each point another point on the plane (to be precise, they were functions of a complex variable). Stokes had devised a way of finding asymptotic approximations that worked for a whole range of such functions, including the one first described by Airy. Stokes noticed that as you move your variable around the plane, small exponential terms can suddenly pop up and then grow to completely change the nature of the approximation. This happens as your variable traverses certain lines now called Stokes line. (See this article for more details on the so-called Stokes phenomenon.)
This sudden appearance of small exponential terms is a kind of mathematical rebellion, explains Howls. "What is happening here is that [your approximation] is trying to represent the function [you are approximating] with things that are not quite right. So the mathematics rebels and says hang on a minute, you have forgotten those exponentially small terms. But I am telling you that they are there and you need to include them."
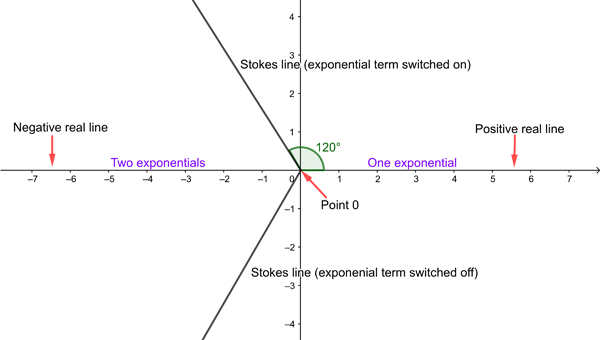
Imagine starting on the positive real line and walking anticlockwise along a circle. As you start off your asymptotic approximation features just one small exponential term, which keeps growing until you reach the Stokes like at angle 120 degrees, where it is maximal. Here the second small exponential is switched on and starts to grow, so that by the time you get to the negative real line both exponential terms are contributing to the value of the approximation. When you reach the second Stokes like at 240 degrees, one exponential is switched off again. See this article to find out more.
The thrill of the infinite
One interesting aspect to Stokes' work lies at the heart of asymptotic approximations more generally. The asymptotic approximation for the type of function Stokes was considering uses infinitely long sums (which mathematicians call series). As you add up more and more terms of the kind of sum used by Stokes, the results you get eventually get larger and larger, exceeding all bounds. The series is said to diverge. If, however, you only consider exactly the right number of terms of such a sum, then the result gives you a very good asymptotic approximation to the function in question. (Find out more here.)
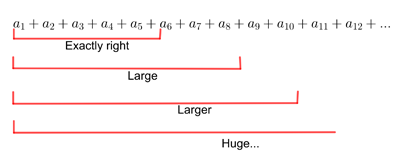
When you add up more and more of the initial terms of a sum that diverges to infinity, you get larger and larger results, eventually exceeding all bounds. It's possible, however that when you consider exactly the right number of initial terms, the result gives you a good approximation for a function you are interested in.
At Stokes' time people were anxious about using divergent series to approximate functions, even calling them an "invention of the devil". But in 1886 the French mathematician Henri Poincaré came up with a rigorous treatment of Stokes' idea, stipulating exactly what he meant by the asymptotic expansion of a function, and showing that you can work with these expansions in a meaningful way even though they are made of divergent series (see here to find out more).
Reading the secret code
Stokes's achievement regarding asymptotic approximations had been to spot that births (and deaths) of exponential terms were possible at all, and to figure out that if they occur, they do so as your variable crosses a Stokes line. What he hadn't been able to explain were the mathematical workings of exactly how those exponential terms are born and die.
This question wasn't picked up again until over 100 years later, among others by the theoretical physicist Robert Balson Dingle, who also happens to be Howls' academic grandfather: he supervised the PhD of Howls' own PhD supervisor Michael Berry.

Small things can cause big waves — and waves can be understood using asymptotic methods. Photo: David Restivo, CC BY-SA 2.0.
As a physicist, Dingle often came across functions that needed to be approximated using asymptotic techniques — it was too hard to evaluate them exactly. He realised Poincaré's asymptotic expansions had huge potential, but that Poincaré's prescription of how to use them didn't quite go far enough. Used as Poincaré had described, the asymptotic approximation of a function would be too crude to discern any exponentially small terms that might be contributing to the value of the function. Such contributions would live within the difference between approximation and actual function: and even though Poincaré had told us how to estimate the size of this difference (the remainder), this size is so large that any exponentially small terms within it are mere drops in the ocean: you can't discern them, let alone see what they are doing.
Poincaré's asymptotic approximations, just like Stokes's, came from truncating the infinite series involved at just the right point. He didn't pay much attention to the later terms of the series, seeing that they belong to the supposedly useless divergent tail. But Dingle realised that more information can be squeezed out of these later terms: they display a sort of universal structure, which holds clues about the exponentially small terms the approximation neglects, and can be exploited for better accuracy. The remainder, neatly estimated by Dingle, was now small enough to discern the action of those exponentially small terms. The exact mathematical nature of the remainder shows how the terms are generated when the variable crosses a Stokes line. It therefore sheds light on the mathematical rebellion Stokes had identified.
"This was the whole purpose of Dingle's work: to show that the late terms are like a code for what should be there," says Howls. "The [late terms] want to rebel [that's why they diverge], but if you unpick this code, you can find out why they are rebelling. All the information is there in those late terms." (The details of Dingle' work are too technical to be presented here, but if you have the mathematical stomach you can read Dingle's book on the subject.)
Dingle's work holds for a whole range of mathematical functions you might want to approximate using asymptotics. It has since been extended significantly by Howls, his supervisor Michael Berry, and many others working in the field of asymptotic analysis, making it more general and illuminating Stokes' phenomenon in ever more detail. For example, thanks to Berry we know that the exponential terms aren't born suddenly as you cross a Stokes line (as Stokes had thought) but are phased in smoothly, albeit very quickly.
Parallel worlds
Howls' research, and that of his colleagues in the field, has many applications outside of maths. "Any [problem involving waves], if you can't solve it exactly, is highly likely to involve these exponentially small things, that is, exponential asymptotics," says Howls. Waves occur in all sorts of circumstances, of course, and Howls has himself worked on a range of applied mathematical problems, from figuring out how water waves break to modelling jet engines.
But while applied mathematicians working in the field have developed their own techniques, another group of people have also been interested in asymptotic approximation: theoretical physicists in search of a much coveted theory of everything. Unaware of the work done by applied mathematicians, these theoretical physicists sought the help of an approach which was developed, roughly in parallel, by the French mathematician Jean Ecalle — it's called resurgence theory.
"Resurgence is a very elegant and comprehensive theory, which has been going for over 30 years now," says Howls, but admits that he at first found the mathematics a little hard to penetrate. When he went to a research conference at CERN, home of the Large Hadron Collider, in 2014 he met Ines Aniceto and discovered that theoretical physicists had had more luck with Ecalle's theory. "Ines pulled me up short in one of my lectures and said 'why don't you do it this way?' It became very clear to me that the physicists understood Ecalle's work and had turned it into something you can do practical calculations with."
Creating breakthroughs
Aniceto is now one of Howls' co-organisers for the current research programme at the Isaac Newton Institute, along with Adri Olde Daalhuis and others. Its aim is to combine the knowledge of applied mathematicians and theoretical physicists that has been developed over the past 25 years. "From the applied maths point we are hoping to learn the more intricate details and powerful techniques from resurgence theory," says Howls. "It's about cross-over. My knowledge of the field has dramatically increased through having worked with Ines and her co-workers. Even today we were discussing a problem that we hope will make a bit of a breakthrough in combining the techniques."
The knowledge transfer, says Aniceto, will equally benefit theoretical physics. "There is an immense world of phenomena that have been studied in applied maths with asymptotic methods," she told Dan Aspel from the Isaac Newton Institute in an interview. "[Some of these] are still lacking from the point of view of the physics, but are desperately needed. So the transfer also goes from applied maths to theoretical physics. [It will create] major breakthroughs in the world of physics as well."
When those breakthroughs happen we will be sure to report on them.
About this article
This article relates to the Applicable resurgent asymptotics research programme hosted by the Isaac Newton Institute for Mathematical Sciences (INI). You can see more articles relating to the programme here.
Marianne Freiberger is Editor of Plus. She interviewed Chris Howls in July 2021.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
