Group theory is essentially the study of symmetry. It underpins much of modern mathematics and is also hugely relevant to other areas — from physics to computer science. And although the field is over two hundred years old, it's still a vibrant and dynamic area in which exciting things are happening right now.
This is why the Isaac Newton Institute (INI) in Cambridge is running a research programme called Groups, representations and applications (GRA), which focusses on the wealth of new results and directions in the area. In this article two of the programme's organisers Colva Roney-Dougal and Martin Liebeck, tell us what their programme is all about.
What's a group?
Groups are a staple of mathematics. You may not have come across them at school, but the general idea behind them is not too hard to understand. A group is a self-contained collection of objects, together with a way of combining any two objects to get a third, which follows certain rules. As an example, take the integers, together with the operation of addition. When you add two integers you get another integer, so the collection of integers is self-contained under addition. There's a special integer, 0, which when you add it to any other (such as 12) leaves that other integer unchanged (12+0=12). And given any integer (such as 12) there's another integer (-12) such that when you add the two you get the special integer 0 as a result (12+(-12)=0).

This table represents a group called the Klein 4 group. The letter e stands for the special element corresponding to 0 in our example of the integers. If you want to know what you get when you combine, say, element b with element c, you find the entry corresponding to the column labelled b and the row labelled c, which is a.
Any collection of objects, together with an operation that combines any two objects, which behaves in this way and satisfies one other rule, is called a group. You can see the precise definition of a group here.
Groups turn up all over the place, in mathematics and also outside it. However, pure mathematicians like to study groups as abstract objects, regardless of what context they might arise in (see the table on the right for an example of an abstract group). Group theory is the study of such abstracts groups.
Keep it simple
There's an infinite zoo of different groups out there, so at first understanding them all seems impossible. However, when you are dealing with a finite group (one with only finitely many elements), then one tool at your disposal is to break it up into subgroups. These are collections of elements from the bigger group, which themselves form a group. Any finite group can be decomposed into a number of finite simple groups, which themselves can't be broken up any further.

Martin Liebeck and Colva Roney-Dougal.
This table represents a group called the Klein 4 group. The letter e stands for the special element corresponding to 0 in our example of the integers. If you want to know what you get when you combine, say, element b with element c, you find the entry corresponding to the column labelled b and the row labelled c, which is a.
You can think of finite simple group as atoms of group theory. Or, to use a mathematical analogy, breaking a group down into finite simple groups is a bit like factorising an integer into its prime factors: since you know that any integer can be factorised into primes in a unique way, studying just the primes can give you a lot of insight into all integers.
In a similar way, it would be useful to understand all the finite simple groups. "One of the biggest theorems of the twentieth century was the classification of all the finite simple groups," says Martin Liebeck. "The final step was achieved in 2004. This has become a [hugely powerful] tool to be used, both in group theory itself, and in its applications." (You can find out more about the classification of finite simple groups in this article.)
But although the finite simple groups have now been classified, giving something like a periodic table for group theory, there are still many things about them mathematicians would like to study. "We know the names of all of the simple groups, but [would like] to understand more about their structure and the ways they can behave," says Colva Roney-Dougal. "[And we would like to understand] how we can use the knowledge of that structure to solve all kinds of problems that are not immediately to do with group theory, but pull out into [other areas of maths]." This is why the theory of simple groups is one main aspects of the GRA programme.
Representation is key
One thing that can be a bit puzzling about groups is that two groups made up of completely different objects — one made from numbers and one from rotations of the plane, for example — can nevertheless be the same. That's because a group is defined by the way its elements interact through the operation that combines any two elements, not by any context it might arise in (see here to find out more).
You can watch a video interview with Roney-Dougal and Liebeck on the INI website
Given this potential for confusion, when you study abstract groups, it makes sense to agree to talk about them only using one kind of object. Luckily, any group you can possibly think of can be written down in terms of matrices (these are arrays of numbers that can be added and multiplied). There's a whole field of group theory, called representation theory, which deals with how abstract groups can be written down in terms of matrices — and this field is another strand of the GRA programme (find out more here).
"[Representation theory] is a vast subject with lots of applications and connections," says Liebeck. And it's also a field where exciting things are happening right now. There's a collection of long-standing open questions, called the counting conjectures which, thanks to the classification of simple groups, mathematicians are now able to attack.
"These counting conjectures have been around for fifty years now, and just in the last five or ten years there has started to be major progress on them," says Roney-Dougal. "There's a sense now, particularly with this programme, that we have gathered together enough experts in the field that there's a real chance that one of the conjectures may fall [very soon]. That would be awesome."
Computing groups

|
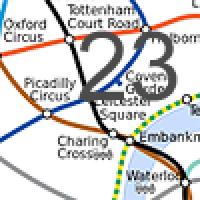
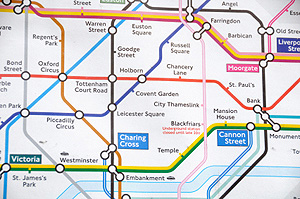 A piece of a geographically accurate map of the London Underground (top, image from Wikimedia commons) and the (roughly) corresponding piece of the network on the actual map (bottom). |
At first sight, group theory might appear to be one of those classical pen-and-paper fields of mathematics, where a computer isn't much help. But that's not true: specially designed computer algorithms can be extremely useful in understanding groups . "Computation is a huge and growing tool in group theory," says Liebeck. "One can test and form conjectures using computation, one can prove special cases of theorems using computations, and one can even get ideas of how to prove general [results] from computation. There's a big interplay between the field of designing algorithms in algebra and the theory of simple groups and representations."
A nice connection between group theory and computer science involves networks. As you can see in the pictures on the right, which both show the London Underground network, the same network can be represented in different ways. If it's just a small network, it's relatively easy to tell if two representations come from the same network, but once the network is large, you'll need a computer algorithm to do it for you. The graph isomorphism problem, loosely speaking, asks if there's an efficient computer algorithm to do this (find out more here).
"There was a major breakthrough [on this problem] in 2018, building on some [deep results] to do with the classification of finite simple groups," says Roney-Dougal. "There are many questions related to graph isomorphism where now we are wondering whether, again, using deep results about the classification of finite simple groups, it might be possible [to make progress on]." That's another theme the GRA programme is focussing on.
Applications
A fourth strand of the GRA programme is about the applications of group theory. One of them is the shuffling of cards. Shuffling a pack amounts to permuting the order of the cards, and the collection of permutations of a set of objects forms a group.
We explore some of the maths of shuffling in this article, based on a lecture by an eminent participant of the programme, Cheryl Praeger. The GRA programme also includes a pioneer in the field, Persi Diaconis, who has put his research to practical use in work with casinos.
Besides shuffling there are many other applications of group theory, particularly in other areas of maths, and many of them are being explored by the GRA programme.
Due to the COVID-19 pandemic, the GRA problem was put on hold in March 2020, after having got off to a flying start in January that year. But as soon as it's safe to do so, the programme will resume. We'll be sure to report on any exciting developments that result, so watch this space. In the meantime, you can read selected articles about groups relevant to the GRA programme here.
Return to the Plus advent calendar 2021.
About this article
This article is based on an interview with Colva Roney-Dougal and Martin Liebeck produced by the Isaac Newton Institute.
Colva Roney-Dougal is Professor of Pure Mathematics and Director of the Centre for Interdisciplinary Research in Computational Algebra at the university of St Andrews.
Martin Liebeck is Professor of Pure Mathematics and Head of the Pure Mathematics Section at Imperial College, London.
Marianne Freiberger is Editor of Plus.
This article is part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI), an international research centre and our neighbour here on the University of Cambridge's maths campus. INI attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
