Maths in a minute: The graph isomorphism problem

Networks are everywhere. We encounter them every day, in the form of the internet, or the social, transport and utility networks we depend upon. Mathematically, a network is an example of a graph: a collection of nodes (also called vertices) connected up by links (also called edges). The problem is that the same graph can appear in different guises — which prompts the question of how hard it is to tell whether two apparently different graphs are actually the same. That question is known as the graph isomorphism problem.

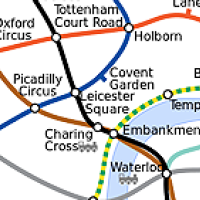
A piece of a geographically accurate map of the London Underground (top, image from Wikimedia commons) and the (roughly) corresponding piece of the network on the actual map (bottom).

An example of two graphs that look different but are actually the same comes from the London Underground map. The relative locations of the stations have been changed, compared to the geographical map, to make it easier to read (find out more here). The Underground network on the tube map looks different from what it looks like when drawn accurately, yet the two are isomorphic: you can match each vertex and each edge from one graph exactly to a vertex or edge in the other (and vice versa), in a way that preserves the connectivity of the graph (which vertex is linked to which). In this example we know from the start that the two networks are isomorphic, after all they represent the same physical train network, but without the context it might have taken us a while to figure out that they really are.

The graph isomorphism problem doesn't ask whether it's possible spot if two graphs, given by different representations, are isomorphic. There are algorithms, step-by-step recipes, which can do just that. Rather, the question is whether there is an algorithm that is faster than the ones that are known. Mathematicians have a way of ranking problems according to their difficulty (more precisely, their complexity). The graph isomorphism problem asks where in the hierarchy of complexity classes the graph question belongs. Although an answer wouldn't have many practical uses (people have long known of algorithms that efficiently solve the problem for the vast majority of graphs they come across in the real world), it's a biggie in complexity theory and theoretical computer science. You can find out more about the graph isomorphism problem in Middle class problems and about complexity classes in Not just a matter of time.