
Imagine you are flying a plane on a secret mission. How can you minimise your chance of being captured by an adversary on the ground using radar? That's one of the question discussed by mathematicians, experts from industry, and the Defence Science and Technology Laboratory (Dstl) at a recent event organised by the Newton Gateway for Mathematics. The working group used sophisticated mathematics to come up with solutions to this tricky real-world problem, but the general idea was inspired by some basic geometry. Here's how.
The ground rules
Let's consider the following slightly simplified set-up. Imagine a radar system on the ground consisting of a transmitter which can send out short radar pulses, we'll call them pings, that travel out in all directions. There are also a number of receivers which can detect the pings. Each receiver knows how far away it is from the transmitter, and it also knows the exact time at which the transmitter sends out a ping.
A transmitter sends out a signal which can be detected by a receiver.
Now imagine your plane is somewhere within range of the transmitter and the receivers. As a radar pulse hits the plane it scatters off in many different directions. If a receiver is in the path of such a reflected ping, it'll detect it. Since such a reflected ping will arrive at the receiver later than the original unreflected ping (it has a longer distance to travel) the receiver can tell a reflected ping from the unreflected ping. The distance travelled by the reflected ping is the distance between the transmitter and your plane plus the distance between your plane and the receiver.
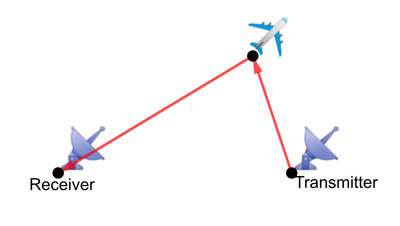
A ping being reflected by a plane. The distance the ping travels is the distance between the transmitter and the plane plus the distance between the plane and the receiver.
Your plane is in the air and the radar system on the ground, so we are working within 3D space. To make the maths a little easier, let's simplify the situation and imagine we're only working in 2D space. This would mean that your plane is on the ground, which isn't where a plane is meant to be, but making this simplification doesn't really matter much as far as our results are concerned. It's possible to generalise them back to 3D, as we will see at the end of the following section.
How they can spot you
Now imagine a receiver detects a ping that was reflected off an object. It knows that the ping has travelled at the speed of light, $c$, which is roughly 300,000 kilometres per second. It knows this because radar is made up of radio waves which travel at the same speed as light does (both light and radio waves are forms of \emph{electromagnetic radiation}).
Because the receiver also knows exactly when the transmitter sent out the ping, it can work out for how long the ping travelled before reaching the receiver: to do this, it just needs to check its watch when the ping arrives.
Since the distance the ping has travelled is equal to the speed it travelled at, $c$, times the time it took to travel, which we call $t$, the receiver now knows the ping has travelled a distance $$d=t\times c.$$
As we already noted above, the distance $d$ is equal to the distance between transmitter and object plus the distance between object and receiver.
This means that the object (your plane) could be at all those points on the ground for which the distance to the transmitter and the distance to the receiver add up to $d$. Long before the invention of radar, the ancient Greeks already knew what kind of a shape is formed by all these possible locations taken together: it's an ellipse.
The mathematical definition of an ellipse is as follows. Suppose you are given two points $T$ and $R$ in the 2D plane and a number $d$ that is greater than the distance between $T$ and $R$. Then the set of all points whose distances to $T$ and $R$ add up to $d$ forms an ellipse. The points $T$ and $R$ are called the \emph{foci} of the ellipse.
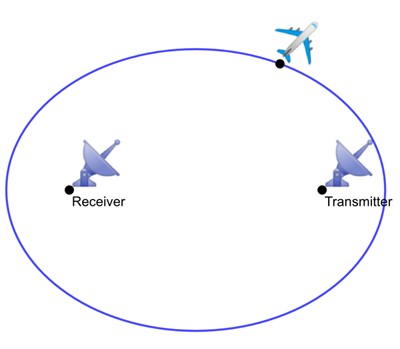
The possible locations of the plane form an ellipse with the locations of transmitter and receiver as foci.
In our example, the points $T$ and $R$ correspond to the locations of the receiver and the transmitter. The receiver therefore knows that the object the ping has been reflected off lies somewhere on an ellipse whose foci are its own location and the location of the transmitter. By imposing a coordinate system on the piece of land we're concerned with, the receiver can work out the equation describing this ellipse, so it knows the exact coordinates of every point on the ellipse, that is, of all the possible locations of the object. (We won't do this now, but you can find out more here.)
Now imagine that a second receiver also detects a reflection of the original ping. Just as the first receiver, it knows that the object lies on an ellipse whose foci are its own location and that of the transmitter. We now have two distinct ellipses the object must lie on, which means that the object must be located at a point at which the two ellipses intersect. In general, two ellipses can intersect at up to four points (to see this, imagine the two ellipses arranged like a cross). However, if the two ellipses share a focus, which is the case in our situation, then they can intersect in at most two points. You can convince yourself of this by drawing a few ellipses (for example by using Geogebra), or by deriving a proof using a beautiful geometric argument explained in this article.
This narrows down the location of the object to at most two points: the points at which the two ellipses intersect.
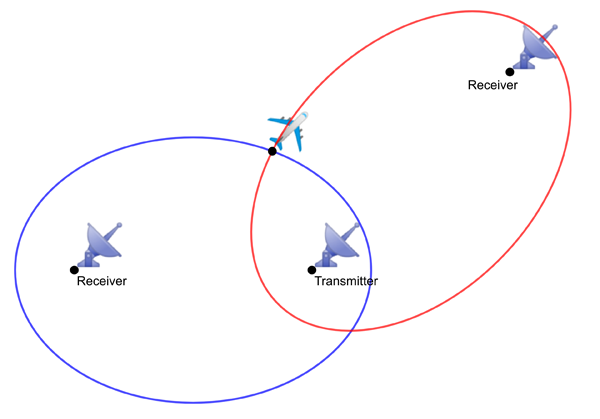
With two receivers the plane must be at one of the two points in which the ellipses intersect.
A third receiver detecting a reflection can nail down the position of the object. It will result in a third ellipse, distinct from the first two, but also having the location of the transmitter as one of its foci. The object must lie on all three of these ellipses — and there is only one point on the plane for which this is true, at least as long as the distance travelled by the third reflected ping is distinct from the first two. If each receiver sends the equation of its ellipse to a control centre, then the control centre can calculate the location of this point. Indeed, a computer can calculate this location in a split second.
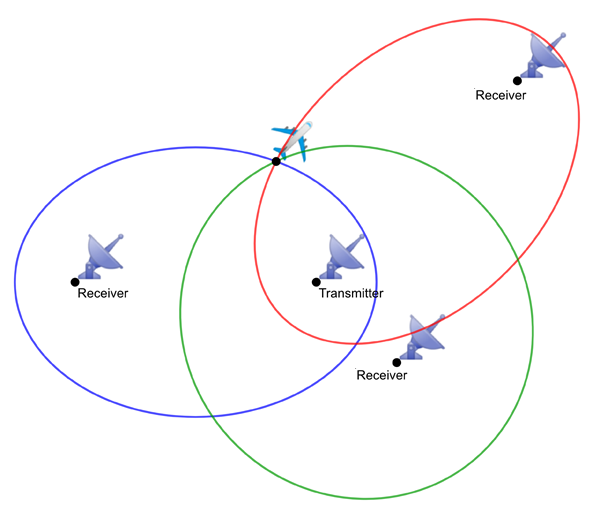
With three receivers the location of the plane is certain: it must be at a point at which all three ellipses intersect, and there's only one such point.
What we have just shown is that, in two dimensions, your location can generally be detected by your adversary if three of the adversary's receivers pick up a ping reflected off your plane. If the adversary has sufficiently many receivers placed cleverly so that sufficiently many of them will always pick up a ping of an object moving through the field of receivers, then you are most definitely going to be spotted.
Before we move on to the next section on how you might fool your adversary, here's a quick word about generalising this scenario to three dimensions. In this case, a receiver picking up a reflected ping can deduce that the object the ping reflected off lies on an spheroid — that's a 3D version of an ellipse which you get by rotating an ellipse around the long axis connecting the two foci. The maths here is more complicated, but generally four intersecting spheroids, that is four receivers, will be sufficient to pin-point the location of the plane in this case.
How you can fool them
One way of hiding from your adversary is to equip your plane with a surface that absorbs a lot of the radar ping and reflects very little, so there isn't much for receivers to detect. But even if you don't have access to such fancy materials, there's a way of fooling your adversary.
Imagine that you are able to detect a radar ping arriving from the transmitter and that you can record it. You could then re-broadcast it with a delay. This would fool your adversary into thinking there are two of you, sitting at two different locations. This would go some way towards avoiding capture: if the adversary decides to come after you, they'd have to split their resources between you and the fictitious object.
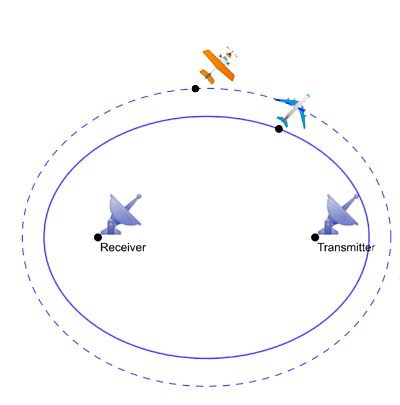
The delayed ping fools a receiver into thinking there's a second object. Because the time it took the delayed ping to travel to the receiver is longer, the inferred distance it supposedly travelled is further. This means the objects must lie on an ellipse whose interior contains the initial ellipse, shown by a dashed curve. If three receivers are fooled by a delayed ping, then your adversary will think the object is sitting at the intersection point of three "false" ellipses, which is different from the true location of the object.
At the Newton Gateway event mathematicians showed that you can go further than that. What we have neglected so far is that, being in a plane, you are actually moving. To identify the trajectory of a moving object, your adversary could send out repeated pings. This would enable them to make an educated guess as to where you're headed, and to try and intercept you.
What the mathematicians showed is that (assuming you are moving at a constant speed in a constant direction) you can time your delayed pings in such a way that the signals received by the adversary's receivers spoof a second object on a trajectory very different to your own. By sending out several batches of delayed pings, you can even trick them into thinking there are several objects, each heading in a different direction. This could be enough to severely confuse your adversary, minimising your chance of being captured.
Beyond the basics
The mathematics used by mathematicians at the Newton Gateway event is more sophisticated than what we described here. Crucially, the mathematicians took account of uncertainties that always arise in a real-world setting. For example, uncertainty enters the picture because receivers can't measure the time of flight of a reflected ping with 100% accuracy, so they can't be 100% sure of the exact location of the object the ping reflected off, and because there are errors associated to the scattering and absorption of electromagnetic radiation off complicated object such as planes.
The mathematicians assumed that, to deal with uncertainty, the adversary would do a statistical analysis of the signals it receives to reveal the most likely location or trajectory of the object. Such an analysis is based on something called Bayes' theorem. The theorem allows you to infer the probability of something happening (eg the plane being in a particular location) based on new evidence (eg a reflected ping) and what you already knew before (eg where you think the plane was a little while ago).
The Newton Gateway event at which this problem was discussed is part of an ongoing programme designed to address a challenge of modern communications. Every country needs to operate effectively across a number of domains — space, air, land, sea and cyber. As in our example of radar, such operations use the electromagnetic spectrum. The problem is that our "electromagnetic environment" has become increasingly congested and contested, due to continuing growth in civilian and military demand for spectrum (for example 5G). The ongoing programme, which along with the Newton Gateway and DSTL involves a firm called PA Consulting, seeks to apply new or alternative mathematics to challenges arising from this problem.
It's nice to know that, although the problems considered at the event are extremely complex, inspiration can come from basic mathematics we have known about for over 2,000 years.
Further reading
You can read more about ellipses and other conic sections here and about geometry more generally here. To find out more about Bayes' theorem see this introduction.
About this article
The New Mathematical Challenges in the Electromagnetic Environment event took place virtually in January 2022, hosted by the Newton Gateway for Mathematics.
Marianne Freiberger is Editor of Plus. She would like to thank Will Handley for help with writing this article.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
