Maths in a minute: Bayes' theorem

Suppose that a particular type of cancer affects 1% of the population. There is a test for this cancer but it's not perfect: although the test gives a positive result for 90% of people who have the cancer, it also gives a positive result for 5% of the people who are cancer-free. You have just received a positive test result – what is the probability you have cancer?

Many of us would say there is now a 90% chance that we have cancer. But this isn't correct – your chances are closer to 15%. To understand why we have to call on conditional probabilities and a very useful result: Bayes' theorem.

A conditional probability is the probability that one thing is true (in this example, that you have this type of cancer) given another thing is true (your test result is positive). For our example we'd write the conditional probability of having this cancer given a positive test result as $P(cancer|positive)$.

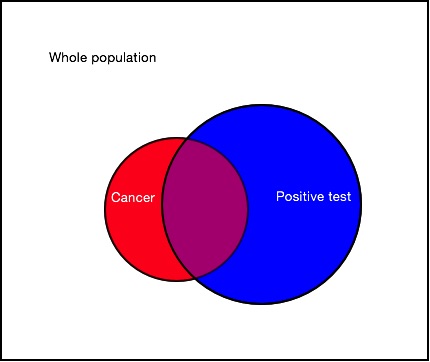
Before you had the test, you believed that your probability of having this cancer was $P(cancer)=0.01$. So, in a population of 10,000 people you'd expect 100 of them to have this cancer. This group of people is represented by the red circle in the picture.

Now you've had a positive test result. How many people out of our population of 10,000 will have had a positive test result – represented by the blue circle in the picture?

There is a 90% chance of a positive test result if you have cancer. For our example population of 10,000 people, 90 out of 100 people with this cancer will receive a positive test result – these people lie in the intersection of the blue and red circles.

And there is a 5% chance that you'll still get a positive test if you are cancer-free – these people lie in the blue circle that is outside of the red circle in the picture. So for the 9,900 cancer-free patients in our population, 495 will incorrectly test positive. This gives a total of $90+495=585$ people out of every 10,000 people expected to get a positive test.

So what is $P(cancer|positive)$, the probability of you having this cancer, given you've had a positive test result? This is the proportion of people who have cancer and have had a positive test result (the intersection of the two circles) of all the people who've had a positive test result (the blue circle): $90/585=0.154$. Or written in terms of probabilities $$P(cancer|positive)=\frac{P(cancer)P(positive|cancer)}{P(positive)}=\frac{0.01\times 0.9}{0.0585}=0.154.$$ where $P(positive|cancer)$ is the probability of getting a positive test result given you do have cancer.

So your chance of having this cancer given you've had a positive test result is a much more encouraging 15%. This result is known as Bayes' Theorem, written more generally as $$P(A|B)=\frac{P(A)P(B|A)}{P(B)}$$ Bayes' theorem allows you to update your prior belief (in this case, that your chance of having cancer was 1%) when new evidence becomes available (a positive test result).

You can read more about conditional probability and Bayes' theorem on Plus.

This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.