As we saw in this introduction to groups, a group is a mathematical object consisting of a collection of things which combine together in a particular way. For example, the integers $\mathbb{Z}$ form a group under addition.

You may have heard of group theory being introduced as the study of symmetry. In this article, we’ll explain precisely what it means for a group to act by symmetries on an object by defining a concept known as a group action.

By a symmetry of an object, mathematicians mean a transformation from the object to itself which leaves all its features unchanged. For example, reflecting a butterfly about its central vertical axis is a symmetry of the butterfly. Switching your two socks around is a symmetry of your socks, because there are no left socks and right socks (thankfully!). Switching your two shoes around, however, would not be a symmetry of your shoes, because your left shoe most likely does not fit on your right foot, and vice versa.

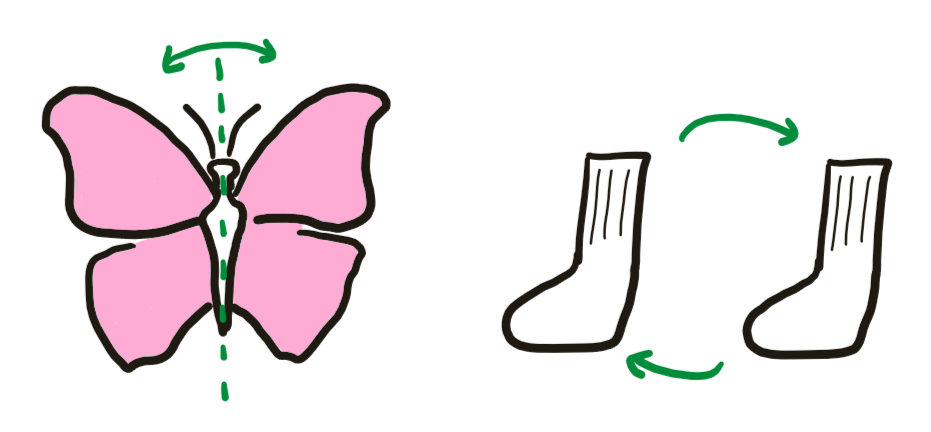
Examples of $C_2$ symmetry.

A group action is a way of assigning elements of a group to symmetries of an object in a way that respects the group operation. We can think of each group element as acting on the object by applying its assigned symmetry, hence the name "group action".

Let’s unpack this with an example: how can the integers $\mathbb{Z}$ under addition act on the number line?

We see that translations by integer amounts are symmetries of the number line.

Integer translations are symmetries of the number line.

A natural way to start might be by assigning the group element 1 the task of shifting the number line to the right by 1:

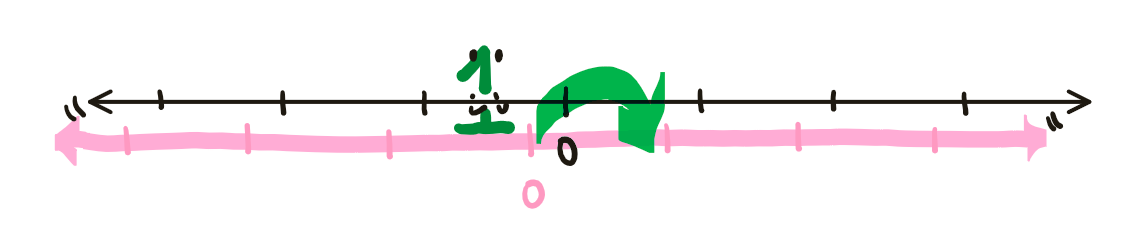
Group action of the element 1

What symmetry should we assign the group element 2? We could try to assign it any old symmetry. But the key to a group action is that the way we assign symmetries must respect the structure of our group. In this case, our group is $\mathbb{Z}$, and the operation is +. Since 2 = 1+1, applying the symmetry assigned to 2 has to be the same as applying the symmetry assigned to 1, then applying the symmetry assigned to 1 again. That is, if f is our rule for assigning symmetries to elements of $\mathbb{Z}$, we want $f(2) = f(1) \circ f(1)$. Thus, we must assign 2 the action of shifting the number line two to the right. Similarly, 3 = 1+1+1, so 3 must shift the number line 3 to the right, and so on.

What about 0? 0 plays a special role in the group $\mathbb{Z}$: it is the identity element. Adding 0 to any integer gives us back the same integer. That is, adding 0 changes nothing. Under the group action, this means that applying the symmetry assigned to 0 must change nothing as well: it must be the identity symmetry.

Now, 0 = 1 + (-1), so applying the action of 1, then applying the action of -1, must get us back to our original position. Hence the action of -1 must be to shift the number line one to the left. Similarly, -2 must shift the number line two to the left, and so on.

Hurray! We have worked out a group action of the integers on the number line: the integer $n$ shifts the number line to the right by $n$.

Notice that we did not have to assign 1 the task of shifting the number line one to the right. We could also have let it shift the number line 2 to the right, or 3 to the right, or even 1 to the left! In each case, updating the actions of all the other elements of $\mathbb{Z}$ accordingly gives another valid group action. Thus, the same group can act on the same object in many different ways.

In general, if $f$ is our way of assigning elements of a group to symmetries of our object, we want $f$ to satisfy $f(ab) = f(b) \circ f(a)$ (remember that function composition reads right to left). Mathematicians call $f$ a homomorphism, which is Greek for shape-preserving. That is, $f$ preserves the shape, or structure, of the group. A more precise definition of a group action is then as follows: A group action of a group $G$ on a set $X$ is a homomorphism from $G$ to the group of symmetries of $X$, $\text{Sym}(X)$.

Other examples of group actions:

• As we saw earlier, $C_2$ acts on butterflies by reflection, and on your socks by switching them around. The same group can act on many different objects!
• $S^1$, the group of all rotations of a plane about the origin, acts on a top by rotating it.
  

  Action of $S^1$ on a top

Notice that we can have any group act on any object by assigning every group element the monumental task of doing nothing. Doing nothing twice in a row is the same as doing nothing once in a row, so the group operation is always technically respected. However, this is not so interesting. To avoid this, mathematicians call a group action faithful if no two group elements are assigned the same task. With this language, we can make precise what it means for a group to be a group of symmetries of an object: there is a faithful group action of the group on the object.

Where to next?

• Representation theory studies groups by looking at how they act on vector spaces.
• Galois theory studies polynomials by investigating how field automorphisms act on their roots.
• How do groups act on different geometries? Non-Euclidean geometries were first organised by Felix Klein in his Erlangen Programme, which sought to classify geometries by their symmetry groups.

About the Author

Justin Chen is currently studying for his masters in mathematics at the University of Cambridge. He is interested in geometry, topology, and sharing the joy of maths with a wider audience.