Tom Hutchcroft has won a prestigious EMS Prize at the European Congress of Mathematics (ECM) 2024, currently taking place in Seville, Spain!

Ten of these prizes are awarded by the European Mathematical Society every four years at the ECM to mathematicians under the age of 35 in "recognition of exceptional contributions to mathematics". The winners must be of European nationality or have carried out their work in Europe. Hutchcroft is a British citizen and currently professor at the California Institute of Technology in Pasadena. He studied at Cambridge University and did his PhD at the University of British Columbia in Canada, where he also spent time as research fellow at Microsoft, in the company's Research Theory Group in Redmond, Washington.

To get a sense of some of Hutchcroft's work, start by imagining rain falling gently to the ground, the water trickling away through the soil. If the rain gets stronger or goes on for a long time, then the soil will become logged. The water will no longer percolate through it, and the ground will flood. You can imagine a layer of soil as a network of little tunnels the water can flow through. It's tunnels becoming blocked that stops the water from draining.

You can build a geometric model of this situation by imagining a collection of points arranged in space. For each pair of neighbouring points you decide whether or not to draw a line between them (representing an open tunnel). To capture the random nature of soil structure, you make this decision at random, drawing a line with probability $p$ (which we take to be the same for all pairs of points). Once you've finished doing this for all points, the proportion of neighbouring pairs of points that are connected is roughly equal to $p$ (as long as there are a lot of points to start with.)

In this percolation model points (not actually shown) were arranged in a square grid in the plane. Neighbouring points were connected with probability $p=0.51$. Figure: Erzbischof, CC BY-SA 3.0.

If $p=0$ then no points are connected (the ground is completely logged). If $p=1$ then all pairs of points are connected (so the water drains away easily). As $p$ gets smaller moving away from 1, more and more connections disappear (so drainage becomes more difficult). A question you can ask is whether there's a critical probability $p_c$, at which the overall nature of the network flips from containing a large connected component (so the water can find a way though) to being broken up into lots of small fragments (so the water can no longer find its way).

What we've just described is an example of a percolation model. Such models aren't just useful to understand how liquids move through porous materials. During the COVID-19 pandemic, for example, we reported how researchers used a percolation model to see what proportion of social contacts should better not happen to stop the infection from sweeping through the entire population. Here the nodes in the network represented households and links between nodes social contacts between them. The idea was to find the critical value $p_c$ at which the network breaks up into fragments, so that any outbreaks would remain confined to those fragments.

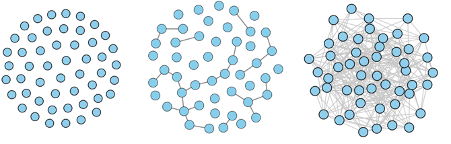
In the left image $p=0$ and all links have been removed. In the image on the right $p=1$ and we a network with a giant component. In the centre image$p=p_c$, where the network undergoes a phase transition, and the giant component appears/disappears. (Image from Kawamoto et. al. 2015 CC BY 4.0

Beyond such concrete applications, there's also something more fundamental to percolation models. They can show a geometric version of what physicists call phase transitions: sudden and drastic changes that can happen in physical systems when a critical threshold is passed. Examples are water starting to boil when the temperature exceeds 100 degrees, or freezing to ice when the temperature falls below 0 degrees. Another example is a material, such as iron, losing its magnetic properties once the temperature gets beyond a critical value. It's been suggested that even the entire Universe underwent a phase transition shortly after the Big Bang, which gave rise to the fundamental forces as we observe them today.

Phase transitions typically involve the random behaviour of gazillions of small components of a system, such as atoms and molecules, so there's no hope of describing them exactly. This is where mathematical models, simplifications of reality that still capture essential features, can help.

Tom Hutchcroft

Although inspired by physics, percolation models come with such rich and interesting mathematics that their study has become a mathematical field in its own right. We already reported on two Fields Medals, even more prestigious awards than the EMS Prizes, being awarded for work in this area: one for Stanislav Smirnov in 2010 and one for Hugo Duminil-Copin in 2022.

The percolation models studied by mathematicians are usually assumed to be made up of an infinite number of nodes. This tends to make the maths easier, and also reflects the fact that physical systems that undergo phase transitions tend to be made up of a huge number of components. In many such infinite percolation models the critical probability $p_c$ where the network changes its nature does exist, so the system does undergo a phase transition at this value of $p$

One fascinating thing about such percolation models that has been important to Hutchcroft's work is that although one model can look very different from the next (there are lots of ways of arranging the nodes in space and lots of possible configurations of links), near the critical probability many features of the models are the same. These features only depend on the large-scale geometry of the networks, rather than their fine details. The phenomenon is known as universality and in some sense justifies the effort of mathematical modelling: although a model will only ever be a simplification of reality, universality means there's a chance that its behaviour reflects what would happen in more sophisticated models that describe reality more accurately.

While universality is central to Hutchcroft's work, one of his most celebrated pieces of work goes in the other direction. In around 2008 the mathematician Oded Schramm proposed that (for certain models under certain conditions) the critical probability $p_c$ should be determined entirely by the small-scale geometry of the network, which you see when you zoom in, not the large-scale structure. Together with his PhD student Philip Easo HT was able to prove this so-called Schramm locality conjecture, 25 year after it had first been posed and to great acclaim.

Tom Hutchcroft was awarded the Prize in front of a packed auditorium in Seville's beautiful Teatro de la Maestranza, in an opening ceremony that also featured a music by the renowned flamenco pianist Dorantes and dance. He will be giving his lecture later on in the week, and we're also hoping to snatch an interview with him for our podcast, so stay tuned!

Congratulations!

This content was produced in a collaboration with the London Mathematical Society.