The maths of randomness: universality

Despite the fact that randomness is surprisingly hard to define, we do have a well defined way of describing randomness mathematically with probability theory. (You can read more in the previous article.) And there are two guiding principles in understanding probabilities: symmetry and universality.

Universality, the second guiding principle in understanding probability, is a more subtle concept than symmetry. (You can read about the principle of symmetry here.) The idea of universality is that that if an outcome is a consequence of many different sources of randomness, then the details of the underlying mechanisms should not matter.

At larger scales

The behaviour of all fluids can be described by the same mathematics.

This concept comes from theoretical physics. Fluids, for example, all behave in much the same way, even though they are made up of molecules with very different shapes and properties. If you look at the molecules in two different fluids microscopically, you would find that they look very different. If you looked at how the two fluids behave at large scales, however, you would see very similar behaviour. The behaviour of all fluids can be described with the same mathematical model, and one which has which has only a few parameters. (You can read more about fluid mechanics in Going with the flow and Maths in a minute: The Navier-Stokes equations.)

It's a similar story in probability theory. At large scales information is aggregated and, sometimes, the same mathematics can describe the outcomes of different underlying processes. An example of a mathematical theorem that captures this concept is the central limit theorem. This theorem says if we compound many random quantities, the result will always follow a "bell curve" – the shape of the normal distribution. (You can read more about the central limit theorem here.)

The central limit theorem is universal. It says that a large set of averages of samples of the property you are measuring will follow the normal distribution, even if the distribution of the property you are measuring is itself not normal. The distribution for flipping a coin many times is uniform: you will get it landing heads half the time and tails half the time. But if you flip a coin 100 times and take the average (with 0 for heads and 1 for tails), then flip a coin another 100 times and take the average, and so on, until you have lots of averages, then these averages will be normally distributed with mean 0.5. Similar to the case for fluid dynamics, the microscopic details of the distribution of the underlying property can be ignored, as the macroscopic view of the distribution of averages will always be normal.

Brownian motion

One of the most famous and surprising examples of universality comes from the discovery of Brownian motion. In 1827 the Scottish botanist Robert Brown was looking at pollen grains suspended in water under a microscope. He observed highly irregular motion in the microscopic particles released by the pollen grains that he could not explain. Intrigued, he went on to conduct many experiments, ruling out any external causes for this jittery motion from the surrounding environment or the experimental set-up, and any internal causes, such as the particles being organic. (He observed the same motion in a inorganic particles, such as coal dust.)

This jittery motion – Brownian motion – was independently explained by Albert Einstein and Marian Smoluchowski in 1905: the vibrating fluid molecules in the liquid give tiny kicks to the microscopic particles, and these many independent tiny kicks accumulated to buffet the microparticles about.

The resulting Brownian motion is random – you can't predict with certainty the position of one of these microparticles from one moment to the next. But you can assign a probability distribution describing where a particle might move to. Einstein and Smoluchowski realised that the way this probability distribution changed over time was described by the same mathematics for describing the way heat flows through objects: using Joesph Fourier's heat equation.

This theory came with quantitative predictions that were verified experimentally by Jean Perrin in 1908, not only confirming this description of Brownian motion but settling the debate about the existence of atoms.

The bigger picture

Brownian motion is universal. It is observed in the random motion of many microparticles regardless of the underlying details of the particular shapes of the particles and fluid molecules involved. But this universality extends even further. Brownian motion was actually first mathematically described by French mathematician Louis Bachelier when he was studying financial systems in 1900. Bachelier described the evolution of stock prices as the accumulation of tiny pushes up and down in price resulting from the myriad of trades that take place. Like the movement of the pollen microparticles, the evolution of stock prices is impossible to predict exactly. But we can assign a probability distribution describing how a stock price will change in value, and again the evolution of this probability distribution is described by the heat equation, a discovery that laid the foundation for financial mathematics.

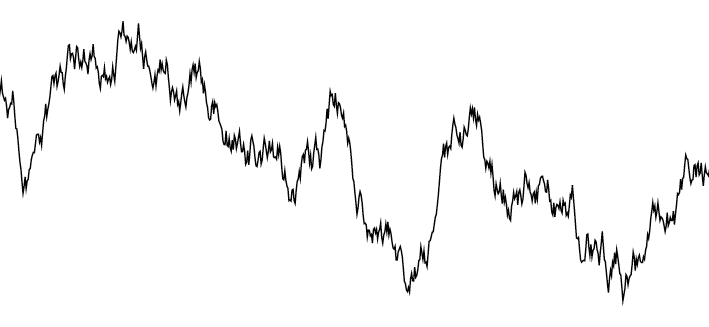
A sample path of Brownian motion

The story of the discovery of Brownian motion, and its universality, illustrates the power of mathematics to describe complicated events using probabilities. It also shows the unexpected and fruitful ways mathematics and physics can inform each other. The principle of universality justifies the study of simplified "toy" models when trying to understand more complicated systems, and highlights the links between seemingly disparate systems.

About this article

Martin Hairer

Martin Hairer is a Professor of Pure Mathematics at Imperial College London. His research is in probability and stochastic analysis and he was awarded the Fields Medal in 2014. This article is based on his lecture at the Heidelberg Laureate Forum in September 2017.