Elections: Could they be fairer?

In a previous article we looked at three voting methods that are relatively simple, but also flawed. We will now have a look at more complex methods. These are more firmly based on mathematical principles with the aim of producing a fairer election.

Condorcet voting methods

Condorcet voting methods are named for the 18th-century French mathematician Marie Jean Antoine Nicolas Caritat, the Marquis de Condorcet who championed what he (and many others) saw as the best possible voting systems. In a pure Condorcet method the choices of each voter are compared against everyone else in a series of "tournaments". If one candidate wins all of the tournaments then they win overall.

Condorcet methods are in a sense the best possible voting systems in elections for which there are many candidates and many voters, who all express views on the candidates.

Let's suppose that each of the voters ranks the candidates in order of preference. Now pick a pair of candidates, say candidate A and candidate B, and check how many voters ranked A above B and how many ranked B above A. The winner of this pairwise contest is the one who was ranked higher more often than the other.

We can make such a comparison for all pairs of candidates. If there is one candidate who wins all of these head to head contests, then it makes sense that this candidate should be declared the overall winner of the election. He or she, if they exist, are called the Condorcet winner.

Using such head to head comparisons in real elections is often unfeasible, as many candidates would mean a lot of comparisons. However, given a simpler method, we can ask ourselves whether it will automatically pick the Condorcet winner, if such a winner exists. Methods that do this are called Condorcet methods. It seems intuitively clear that such voting methods are fair.

Some examples

A few examples will help to see what is going on. We will consider an election with three candidates, A, B and C, and 30 voters. The preferences shown by the voters are as follows (where A>B means that a voter prefers A to B):

Number of voters	Preferences
10	A>B>C
1	A>C>B
5	C>A>B
0	C>B>A
9	B>C>A
5	B>A>C

In this election

A beats B on 16 occasions and B beats A on 14, so A is 2 ahead of B on a head to head.
A beats C on 16 occasions and C beats A on 14, so again A is 2 ahead of C on a head to head.
B beats C on 24 occasions and C beats B on 6, so B is 18 ahead of C on a head to head.

This is illustrated in the diagram below.

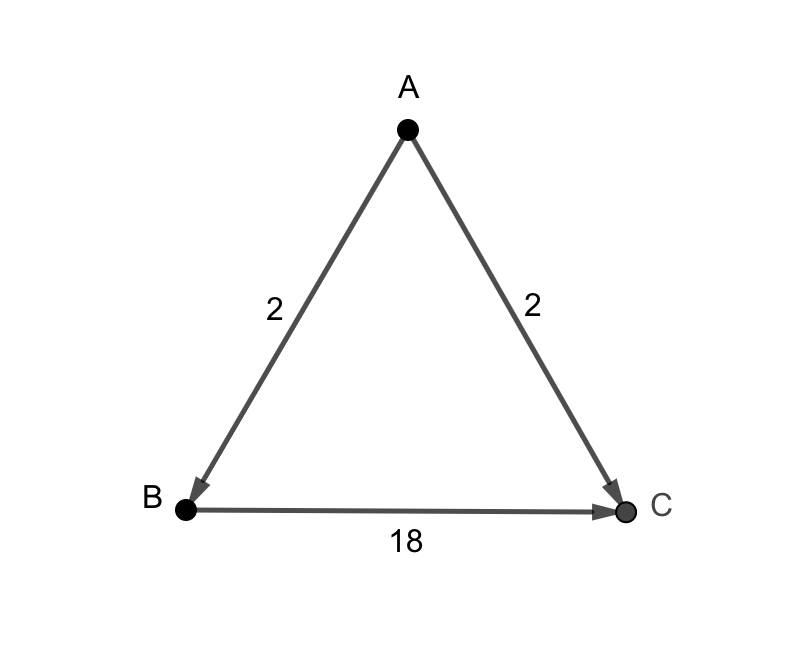
We can see that A is the Condorcet Winner. Hooray.

A first past the post method would give A 11 votes, B 14 votes and C 5 votes. So this would elect B. First past the post is therefore not a Concorcet method.

In an earlier article we looked at the Borda method, which gives each candidate scores depending on how highly a voter ranked them: when there are three candidates, then being ranked first by a voter gives a candidate 2 points, being ranked second 1 point, and being ranked last 0 points. Totalling those scores over all the voters gives the following:

Number of voters	A	B	C
10	2	1	0
1	2	0	1
5	1	0	2
0	0	1	2
9	0	2	1
5	1	2	0
Total	32	38	20

Thus the Borda voting system also elects B (by some margin) over A. It has not found the Condorcet winner and is therefore also not a Condorcet method.

Some problems

Finding a Condorcet winner is often viewed as a gold standard in voting. However, things are not as simple as they might seem. There may be a case when head to head contests always produce a clear winner, but overall there is none. A classic example of this is the game of rock-scissors-paper.

In this example, rock beats scissors, paper beats rock, and scissors beats paper. So who wins? Well no one does. This is called a cyclic situation and there is no Condorcet winner. It is completely symmetric, so there is no way to distinguish between any of the "candidates".

A more complex example is given in the following table:

Number of voters	Preferences
3	A>B>C>D
1	D>B>A>C
1	D>C>A>B
1	C>D>B>A
1	B>D>C>A

The diagram showing the results of head to head contests is given below. In this the arrow from B to C shows, for example, that B has defeated C in a head to head by a margin of 3.

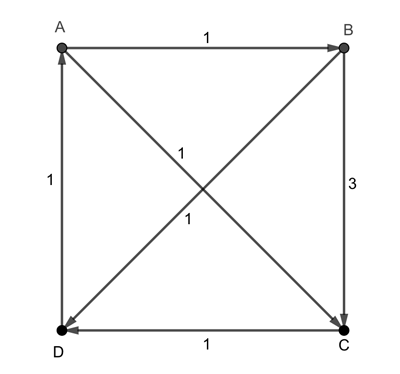
In this case A and B have both won two head to head contests, A with a margin of 1 in both cases and B with a margin of 3 against C and with a margin of 1 against D. C and D have each won one head to head contest. So there is no Condorcet winner.

It is easy to see that in a first past the post election, Party A would get 3 votes, D would get 2 votes, and B and C would get one vote, so A would win overall. A longer calculation shows that in a Borda vote B would just win (with 12 points) over A (with 11 points). So, who has won the election?

Some solutions

A number of voting strategies have been devised which can deal with the cyclic cases and deliver a winner, which will also give the Condorcet winner if one actually exists. Perhaps the earliest of these was devised in 1299 by Ramon Llull and has been reinvented as Copeland's method. This method simply elects the candidate who wins the most head to head contests. In our example above, A and B tie for first place in Copeland's method. Ties are not unusual and mean that the method is not widely used in practice, although a version of it is used in Premier League football.

A much more sophisticated procedure is Schulze's method which was invented in 1997 by Markus Schulze and is now quite widely used. In the Schulze method we draw the same diagram as above, but in the case of (say) A defeating B we put the number of times they have won (in this case 4) on the arrow:

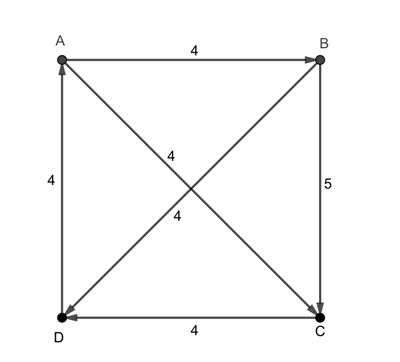
Now for each candidate find a path along the arrows to all of the other candidates. Usually there will be several such paths: in our example above, there are three paths from A to D. One goes via B, one via C, and one via B and C.

The weakest link on any such path is the smallest number on the arrows that make it up. So the weakest link in the path that goes from A to D via B and C is 4. The strongest path is the one which has the largest weakest link. In our example, all three paths have a largest weakest link of 4, so in this case all three paths are equally strong.

The following table shows the weakest link of the strongest path for all pairs of candidates.

	Path to A	Path to B	Path to C	Path to D
Path from A	-	4	4	4
Path from B	4	-	5	4
Path from C	4	4	-	4
Path from D	4	4	4	-

Let's write P(X,Y) for the weakest link of the strongest path from X to Y. Then the winner of a Schulze election is the candidate X so that P(X,Y) > P(Y,X) for all possible Y.

In the election above B is the Schulze winner.

The Schulze method has many other advantages in a voting process, not least of which is that it is comparatively easy to compute. Users of the Schulze method include Debian (2003), Gentoo (2005), Topcoder (2005), Wikimedia (2008), KDE (2008), the Pirate Party of Sweden (2009), and the Pirate Party of Germany (2010).

There are many similar methods to find a Condorcet winner if one exists. These go a long way to being fair, and are based on firm mathematical principles. They are, however, rather sophisticated in the way they arrive at the winner. This is fine if there is either a relatively small number of votes, or where the voting, and hence the processing, can all be done electronically. This is why they have taken off in internet voting.

However, electronic voting has not (yet) been considered for serious political decisions such as national elections, mainly due to issues associated with fraud. Instead, national elections prefer to use a system in which voters cast ballots on paper. These then have to be processed by hand, and the results announced rapidly. This means that practical voting systems have to be used which are a simplification of those considered above.

Of course the simplest of all of these is the first past the post system, which only requires one count of the votes to reach a decision (unless a recount is needed if the voting is close). Given the problems with this, other systems have been devised which have more of the merits of the ideal systems above, but have to make compromises. An example is instant run-off voting. Both first past the post and instant run-off are explored in the previous article. In conclusion we have to admit that all voting systems are flawed in some way. Deciding what kinds of flaws we are happy to live with, and what kinds we prefer to avoid, is the most important mathematical task of a democracy.

---

---

About this article

This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.

He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.