
Elections: Three common methods
In the previous article we saw that no voting method can ever be completely fair. In this article we will look at three voting methods that are widely used in practice but, as is to be expected, come with flaws.
First past the post
This article is based on a talk in an ongoing Gresham College lecture series. You can see a video of the talk below.
This is the simplest of all systems. In its purest form the voters are presented with a list of candidates or policies. They express a single preference (including abstaining) and the candidate or policy with most votes wins. This is used in each parliamentary constituency in a UK general election. It is also used in voting in the UK parliament in a division of the assembly. In this case, when the division bell is rung, the MPs express their vote by going through one of two doors (the Ayes and the Nays), where the votes are counted by Tellers.
A very similar process was used in the Brexit referendum, where the voters were asked simply whether they wanted to leave or remain.
The first past the post method has been used for a long time, and we are very used to it. It has the significant merits of being easy and transparent to use and of usually producing a clear answer. However even in this simple case it is severely flawed.
One obvious problem is that is an all-or-nothing method. Voters are asked to make a clear choice between several candidates, and are unable to express any form of preference between them. A second, and related, problem is that similar candidates can split the vote. I experienced this directly during a vote conducted in the 1990s in Bristol about the future funding of education. The voters were asked to give a single vote to one of three options:
- Increase secondary school funding,
- Increase primary school funding,
- Give no extra funding to schools.
As I recall the voting went something like: 25% for 1, 35% for 2, and 40% for 3.
 First past the post is used in UK general elections.
First past the post is used in UK general elections. On the basis of this the Bristol Council concluded that the winner was 3 or "no extra funding". And that is what they did. This was despite the obvious fact that 60% of the people in Bristol had in fact voted for an increase in funding for some form of education.
A third problem is the possibility of error. Crucial decisions can be decided on the basis of a single vote majority. This is fair if everyone votes, but what happens if they don't? For example, the 2016 the Brexit referendum result was 52-48 in favour of Leave, as the observed proportion of Leavers was 51.9%. On this basis, the statement that "the majority of the UK chose to leave the EU" has been made.
If all of the voters had voted then that would be true, but this did not actually happen. The turnout rate was only about 72%, which means that only 37% of the eligible British electorate chose Leave. Any statement about the whole population made on the basis of such a limited sample is at best uncertain. The question must arise as to whether a 52% majority on a 72% sample is strong evidence for a greater than 50% majority from the whole sample. This is a subtle question in statistics and it is a good reason for insisting on a margin of error before a decision based on a referendum is made.
An analysis of the Brexit result in the statistical journal Significance concluded, controversially, that the result could not be distinguished from a tie. As might be expected this has led to a lot of subsequent discussion and I will not enter into this here!
Elections with multiple constituencies
The problems with first past the post are exacerbated when there are multiple constituencies. This happens in both the UK and US elections, where the voters in each constituency vote for a representative from a political party (eg. an MP) using the first past the post system. The party with the largest number of representatives (MPs) then wins the election overall.
This method has two big advantages. Firstly it gives a clear result and (generally) leads to a majority government. Secondly it clearly links the voters to their representative. Neither advantage is to be disregarded lightly.
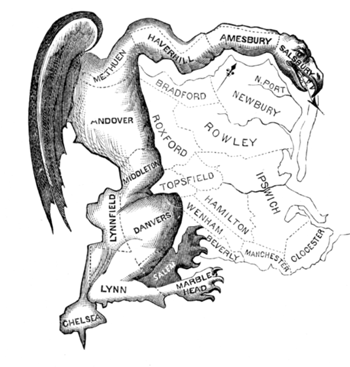
This political cartoon led to the coining of the term "gerrymander". The district depicted in the cartoon was created to favour the incumbent Democratic-Republican party candidates of Governor Elbridge Gerry over the Federalists in 1812.
However, it is easy to see why this system is flawed, using a simple example. Imagine that we have three constituencies with respectively 10,000, 3 and 5 voters and parties A and B. In the first constituency everyone votes for A. In the other two everyone votes for B. Thus party A gets one MP and 10,000 votes, whereas B gets two MPs and 8 votes. Party B wins the election even though it got far fewer votes than party A.
This problem also arises in practice. In the last US presidential election, Donald Trump and the Republicans got 304 electoral votes and 46.1% of the vote, whereas Hilary Clinton and the Democrats got 227 electoral votes and 48.2% of the vote. On this basis the Republicans won, even though the Democrats won the so-called popular vote.
It clearly matters hugely in first past the post elections exactly where your voters are located. Indeed small shifts in the boundaries between constituencies can have big effects in the results of an election. For example, changing the boundary of a constituency so that a group of voters moves from a safe seat to a marginal seat will not affect the safe seat, but could swing the marginal. The practice of gerrymandering arises when the process of moving boundaries is exploited by unscrupulous individuals with the aim of winning elections. It is named after the governor of Massachusetts, Elbridge Gerry, who two centuries ago approved of a new and oddly shaped voting district (illustrated) that was long, thin and curvy, with the explicit outcome of (successfully) trying to rig the election.
After all this it would seem obvious that a better means of voting is needed!
Proportional representation
Proportional representation (PR) is widely held to be a fairer voting system than first past the post in the case of each voter having one preference. PR is used in many places, most notably in the elections to the European Parliament.
In the simplest form of PR the number of representatives of each party is taken to be directly proportional to the number of votes that they get in an election in which the voters express only one preference. For example, if a party wins one third of the votes then it should gain one third of the seats. Simple!

Proportional representation is used in the European Parliament. Photo: Mathieu Cugnot, © European Union 2017 - source:EP.
Sadly not. There are a number of reasons which make a purely proportional system difficult to use in practice. Most notably amongst these is that usually the divisions produce fractional numbers of seats. For example, if there are ten seats and each of three parties gets a third of the votes then the best thing we could do would be to divide the seats up as 3, 3, 4. But why should one party get more than the others?
Another problem is that some parties, or countries in the European elections, may get no representation at all. This is avoided by giving each country a minimum number of seats, which again breaks pure proportionality.
A number of methods have been devised to deal with the issue of fractional seats, by trying to minimise different kinds of disproportionality. Widely used methods are the D'Hondt method and the Webster/Sainte-Laguë method. The former minimises the number of votes that need to be left aside so that the remaining votes are represented exactly proportionally and slightly favours large parties and coalitions over scattered small parties. In comparison, the latter reduces the reward to large parties, and it generally has benefited middle-size parties at the expense of both large and small parties.
We won't explain these methods in detail here. To find out more about the D'Hondt method method, see this Maths in a minute article.
The European Union recognised the role of maths in democracy when in 2011 it sought the advice of a committee of mathematicians to help figure out how to allocate the seats in the European Parliament to member states. Sadly, it didn't head the expert advice that was given. To find out more, see No maths for Europe.
The instant run-off (IRV)
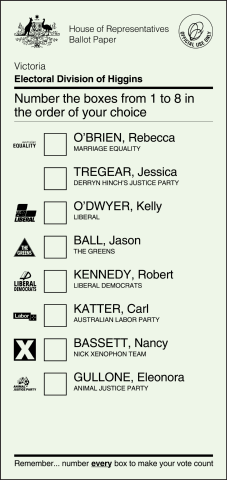
Representation of the ballot papers used at the 2016 Australian federal election in the Division of Higgins. Image: Hshook, CC BY-SA 4.0.
The IRV voting method is used to elect a single candidate in an election. Unlike first past the post and proportional representation it allows the different preferences by the voters for the candidates to be taken into account. This system (versions of which are used in Australia and Ireland where it is called preferential voting) works as follows. We assume as usual that we want to elect one candidate from several alternatives.
- The voters rank each of the candidates in order of preference.
- The ballots are initially counted for each voter's top choice and if a candidate has more than half of the vote based on first choices, that candidate wins.
- If not, then the candidate with the fewest votes is eliminated.
- The voters who selected the defeated candidate as a first choice have their votes for that candidate added to the totals of their next choice.
- This process continues until a candidate has more than half of the votes.
- When the field of candidate is reduced to two, it becomes an instant run-off that allows a comparison of the top two candidates head-to-head.
IRV is used in several national elections. For example, a version is used to elect members of the Australian House of Representatives and at least one house of all Australian state parliaments, the President of India and members of legislative council in India; the President of Ireland, members of Congress in Maine, in the United States; and the Parliament in Papua New Guinea. The method is also used in local elections around the world. The possible use of the system (known as alternative vote in the UK) was put to a referendum of the British public in May 2011, and the motion was defeated.
A simple example (inspired by the Wikipedia article on IRV) is provided in the following table. Three candidates are running for election, A, B and C. There are five voters, a, b, c, d, e. A 1 means that a voter has put a candidate first on their list, a 2 that they have put them second, and a 3 that they have put them third.
| Candidate | a | b | c | d | e |
| A | 1 | 2 | 3 | 1 | 2 |
| B | 3 | 1 | 2 | 3 | 1 |
| C | 2 | 3 | 1 | 2 | 3 |
To win straight out, a candidate must have a majority of first-choice rankings. In Round 1, the first-choice rankings are that A and B both have two votes and C has one. No candidate has a majority, so a second round is required. Since C is in bottom place, they are eliminated. Any voter who ranked C first (e.g. c) has their original second choice candidate turned into their new first choice, and their original third choice becomes their new second choice. This results in the Round 2 votes as seen below. This gives B 3 votes, which is a majority. So the IRV winner is B.
| Candidate | a | b | c | d | e |
| A | 1 | 2 | 2 | 1 | 2 |
| B | 2 | 1 | 1 | 2 | 1 |
As a separate calculation, the Borda winner in this case is A. It can also be shown that whilst IRV satisfies the majority condition, it fails Condorcet winner condition (see the next article to find out what this means). Thus it is far from a perfect voting system.
As we have seen, first past the post, proportional representation, and instant run-off are all flawed. In the next article we will look at methods that are more complex, but based on mathematical principles.
About this article
This article is based on a talk in Budd's ongoing Gresham College lecture series (see video above). You can see other articles based on the talk here.

Chris Budd.
Chris Budd OBE is Professor of Applied Mathematics at the University of Bath, Vice President of the Institute of Mathematics and its Applications, Chair of Mathematics for the Royal Institution and an honorary fellow of the British Science Association. He is particularly interested in applying mathematics to the real world and promoting the public understanding of mathematics.
He has co-written the popular mathematics book Mathematics Galore!, published by Oxford University Press, with C. Sangwin, and features in the book 50 Visions of Mathematics ed. Sam Parc.