How do we hallucinate?

Think drug-induced hallucinations, and the whirly, spirally, tunnel-vision-like patterns of psychedelic imagery immediately spring to mind. But it's not just hallucinogenic drugs like LSD, cannabis or mescaline that conjure up these geometric structures. People have reported seeing them in near-death experiences, as a result of disorders like epilepsy and schizophrenia, following sensory deprivation, or even just after applying pressure to the eyeballs. So common are these geometric hallucinations, that in the last century scientists began asking themselves if they couldn't tell us something fundamental about how our brains are wired up. And it seems that they can.

Computer generated representations of form constants. The top two images represent a funnel and a spiral as seen after taking LSD, the bottom left image is a honeycomb generated by marijuana, and the bottom right image is a cobweb. Image from this paper, used by permission.

Geometric hallucinations were first studied systematically in the 1920s by the German-American psychologist Heinrich Klüver. Klüver's interest in visual perception had led him to experiment with peyote, that cactus made famous by Carlos Castaneda, whose psychoactive ingredient mescaline played an important role in the shamanistic rituals of many central American tribes. Mescaline was well-known for inducing striking visual hallucinations. Popping peyote buttons with his assistant in the laboratory, Klüver noticed the repeating geometric shapes in mescaline-induced hallucinations and classified them into four types, which he called form constants: tunnels and funnels, spirals, lattices including honeycombs and triangles, and cobwebs.

In the 1970s the mathematicians Jack D. Cowan and G. Bard Ermentrout used Klüver's classification to build a theory describing what is going on in our brain when it tricks us into believing that we are seeing geometric patterns. Their theory has since been elaborated by other scientists, including Paul Bressloff, Professor of Mathematical and Computational Neuroscience at the Oxford Centre for Collaborative Applied Mathematics.

How the cortex got its stripes...

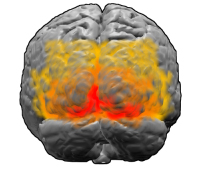
The visual cortex: the area V1 is shown in red. Image: Washington irving

In humans and mammals the first area of the visual cortex to process visual information is known as V1. Experimental evidence, for example from fMRI scans, suggests that Klüver's patterns, too, originate largely in V1, rather than later on in the visual system. Like the rest of the brain, V1 has a complex, crinkly, folded-up structure, but there's a surprisingly straight-forward way of translating what we see in our visual field to neural activity in V1. "If you imagine unfolding [V1]," says Bressloff, "You can think of it as neural tissue a few millimetres thick with various layers of neurons. To a first approximation, the neurons through the depth of the cortex behave in a similar way, so if you compress those neurons together, you can think of V1 as a two-dimensional sheet."

From the visual field to the visual cortex

Think of the visual field as a flat sheet, endowed with polar coordinates: each point $P$ in the field is defined by two numbers $(r, \theta)$, where $r$ is its distance to the origin $O$, and $\theta$ the angle between the line $OP$ and the $x$-axis. The origin corresponds to the centre of the visual field. V1 is also modelled as a flat sheet, this time endowed with the usual Cartesian coordinates $(x,y)$. The exact coordinate map between the visual field and the flat model of V1 is complicated to write down, but for points in the visual field that are away from the centre of the field (so for $r$ sufficiently large) it is similar to the logarithmic map $$x=\ln{r} \;\;\;\;\;\;\;\; y= \theta.$$ This map transforms a circle of radius $r$ in the visual field into a vertical straight line segment at $x=\ln{r}$, and a ray emanating from the origin $O$ at angle $\theta$ into a horizontal straight line segment at $y=\theta$.

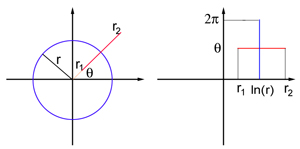
An object or scene in the visual world is projected as a two-dimensional image on the retina of each eye, so what we see can also be treated as flat sheet: the visual field. Every point on this sheet can be pin-pointed by two coordinates, just like a point on a map, or a point on the flat model of V1. The alternating regions of light and dark that make up a geometric hallucination are caused by alternating regions of high and low neural activity in V1 — regions where the neurons are firing very rapidly and regions where they are not firing rapidly.

To translate visual patterns to neural activity, what is needed is a coordinate map, a rule which links each point in the visual field to a point on the flat model of V1. In the 1970s scientists including Cowan came up with just such a map, based on anatomical knowledge of how neurons in the retina communicate with neurons in V1 (see the box on the right for more detail). For each light or dark region in the visual field, the map identifies a region of high or low neural activity in V1.

So how does this retino-cortical map transform Klüver's geometric patterns? It turns out that hallucinations comprising spirals, circles, and rays that emanate from the centre correspond to stripes of neural activity in V1 that are inclined at given angles. Lattices like honeycombs or chequer-boards correspond to hexagonal activity patterns in V1. This in itself might not have appeared particularly exciting, but there was a precedent: stripes and hexagons are exactly what scientists had seen when modelling other instances of pattern formation, for example convection in fluids, or, more strikingly, the emergence of spots and stripes in animal coats.

...and how the leopard got its spots

The first model of pattern formation in animal coats goes back to Alan Turing, better known as the father of modern computer science and Bletchley Park code breaker. Turing wrote down a set of equations which showed how two interacting chemical components that start out in equilibrium, when nudged out of balance, can polarise to form patterns that have a high concentration of one chemical in some regions and a high concentration of the other chemical in others. If those chemicals produce pigments in the skin of an animal embryo, then, voilà, they give you its coat or skin pattern. (See the Plus article How the leopard got its spots for more detail.)

Neural activity in the brain doesn't work in the same way, but there are analogies to Turing's model. Neurons send signals to each other via their output lines called axons. The interaction separates them out into two interacting groups, akin to the two interacting chemicals: there are neurons which are excitatory — they make other neurons more likely to become active — and there are inhibitory neurons, which make other neurons less likely to become active.

Stripy, hexagonal and square patterns of neural activity in V1 generated by a mathematical model. Image from this paper, used by permission.

Inspired by the analogies to Turing's process, Cowan and Ermentrout constructed a model of neural activity in V1, using a set of equations that had been formulated by Cowan and Hugh Wilson. Although the equations are more complicated than Turing's, you can still play the same game, letting the system evolve over time and see if patterns in neural activity evolve. "You find that, under certain circumstances, if you turn up a parameter which represents, for example, the effect of a drug on the cortex, then this leads to a growth of periodic patterns," says Bressloff.

All this suggests that geometric hallucinations are a result of an instability in V1: something, for example the presence of a drug, throws the neural network off its equilibrium, kicking into action a snowballing interaction between excitatory and inhibitory neurons, which then stabilises in a stripy or hexagonal pattern of neural activity in V1. In the visual field we then "see" this pattern in the shape of the geometric structures described by Klüver.

Cowan and Ermentrout's model was only the beginning, and scientists, including Bressloff, have since come up with more sophisticated models, that are more anatomically accurate. To find out more about their results, and for a more in-depth version of this article, see here.

Further reading

You can read a more in-depth version of this article here.

About this article

Paul Bressloff was interviewed by Marianne Freiberger, Editor of Plus, in August 2009.

Paul Bressloff is a University Research Professor in Mathematical Neuroscience at the University of Oxford. He has also been awarded a Royal Society Wolfson Merit Award (2009-2014).

Bressloff has spent the past 20 years working at the multidisciplinary interface between applied mathematics, theoretical physics and neuroscience. The main focus of his work is to understand how the brain functions as a complex dynamical system at multiple spatial and temporal scales in healthy and diseased brains. He has published more than 120 papers in research journals and co-authored one book. He has mentored ten PhD students and four postdocs.