
How to tame uncertainty: Part II
In the first part if this article we identified some major sources of uncertainty associated to mathematical modelling. We'll now see how to quantify this uncertainty.
Getting to grips with uncertainty
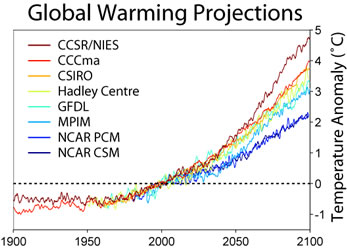
This chart shows the predictions of the future mean temperature from various climate centres around the world. The predictions are not all the same because the models make different assumptions about the level of carbon dioxide and other factors. However, they are all predicting a significant temperature rise by the end of the 21st Century. Find out more abut climate modelling here. Figure reproduced under CC BY-SA 3.0.
"[Quantifying uncertainty] is tough and there isn't a general consensus about what to do in all situations." says Powell. As far as model error is concerned, the best thing you can do is test the hell out of your model to see how it squares up to reality, and continually validate it against all available data. In climate science, for example, models are often started off using the climate conditions from some point in the past and then run forward to predict the conditions of today. If they do this well (and current climate models do), then there's a good chance that they will also give accurate predictions for the future.
When it comes to approximation error, things become inherently mathematical. "A numerical analyst will typically start with a complex model and try and analyse the error associated with an algorithm that has been used to try and approximate the solution," says Powell. "In order to come up with statements about the error, we need to exploit information about the structure of the equations, and we need to make assumptions [about the inputs and the outputs]. This is something we know how to do for simple models, but unfortunately not for very complex models."
Moving forward
The third source of uncertainty, input uncertainty, is typically dealt with using the field of maths that has been specifically designed to deal with chance: probability theory. If you are uncertain about the value of a particular quantity, you can at least try and assign probabilities to the possible values it can take. For example, if the quantity is the mass of the ball in our example above, even if you don't know the exact mass, you might be able to say that it's between 400 grams and 500 grams, and that each value in this range is equally likely to be the correct mass. In that case we say that the mass of the ball is a random variable which is uniformly distributed.

This is Hurricane Isabel, which devastated parts of the US in 2003, as seen from the International Space Station. Forecasters saw this one coming, but in general the weather is very difficult to predict, in part because it suffers from input uncertainty. Find out more here.
Plugging the random variable representing the mass into the equation tells you that the magnitude of the ball's acceleration also lies within a certain range (which depends on the range of the mass and also the magnitude of the force of the roll), and that it is equally likely to take any value within that range.
"This is the basic idea of forward uncertainty quantification," says Powell. "Given a probability distribution for the inputs, how do you propagate it through the model and then estimate something about the solution, given that initial probability distribution?" The information you get out isn't exact, but can still answer important questions. "For example, you [might be able to] get your hands on the probability that the temperature within an engine reaches a critical value which is really bad for the engine," says Powell. At the very least you can get a sense of the impact a change in the parameter might have on the predictions of the model.
In complex models forward uncertainty quantification is of course harder than we have just made out. Choosing a probability distribution can be tricky — ideally, it should be chosen based on data, but if you haven't got much data, you rely on expert judgment. The problem becomes compounded if you only have indirect measurements of the input parameter. This is the case in the ground water example above. "You may not have measurements of the permeability of the rock, but you may have measurements of the pressure of the [ground] water," explains Masoumeh Dashti from the University of Sussex. Inferring the permeability of the rock from measurements of water pressure is akin to trying to work out the shape of an object from a picture of its shadow alone — it's a so-called inverse problem. There are sophisticated mathematical methods for solving inverse problems. Fans of probability theory might like to know that a statistical approach involving Bayes' theorem is currently a hot research topic. It's what Dashti is working on too.
Computing power
Once you have probability distributions for your input parameters you need to propagate them through the model to get your hands on the statistics of the output. But there's a major challenge: the computations can take vast amounts of computing power.
One (though not the only) way of seeing what an uncertain input means for the output of a model is to (metaphorically) draw a particular value of the input out of a hat, then run the model with that particular value to get a single answer. You do this many, many times, making sure the random pick from the hat reflects the probability distribution of the input parameter. This gives you lots of outputs, which together reflect statistical properties of the solution.
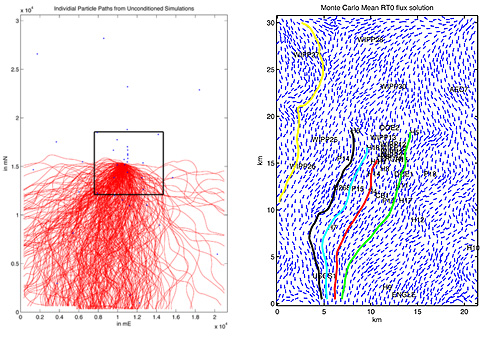
The left panel sows the modelled path of a particle released into a groundwater flow using 300 different values for the permeability of the rock. The right panel shows the mean flow field, a type of average of different possible flows, computed from the model. The coloured lines are trajectories of particles released into the mean flow field. Images: Catherine Powell.
The challenge with complex models is that even only running the model once can take a long time. "For complex models coming from manufacturing, engineering, geophysical applications, for example, each time you are running your model you are talking hours and days of computing time," says Powell. Doing this many, many times, perhaps millions, and then computing something like the average of the output, can take absolutely ages. If you don't use this sampling approach but feed the entire distribution of the input parameter through the model at once, then the model itself becomes vastly more complex and hungry of computing power. The problem won't go away, no matter how you turn.
A lot of effort goes into making the techniques we just mentioned computationally cheaper. Ironically, this involves more approximating, which then introduces more errors that need to be quantified.
So should we trust modelling?
What's clear even from this superficial overview of uncertainty quantification is that it's tricky. So why should we believe the predictions of complex models such as those predicting climate?
"It's very hard for a lay person to have confidence in modelling, especially when we say that the model isn't right, or the numerical method has an error, and so on," admits Powell. This, Powell and Dashti believe, is partly down to poor communication and education. "We don't grow up learning much about uncertainty; there is a perception that the general public can't handle it," says Powell. "As mathematicians we don't know how to do communicate uncertainties well [to a wider audience]. There need to be conversations with people who know more about ethical and philosophical aspects of the [communication of uncertainty]." We also need to promote more success stories of mathematical modelling.
As far as the models themselves are concerned, we should bear in mind that modelling is about prediction and prediction, by its very nature, is uncertain. Good mathematical models are based on the best science and data that is available, are constantly tested against reality and, thanks to mathematicians like Powell and Dashti, even come with an idea of how much their predictions might be out. The models, and the people who make and use them, don't always get it right. But the alternatives are vague guesses, doing nothing, or feigned certainty. And surely nobody would prefer those.
About this article

Catherine Powell.
Catherine Powell is a Reader in Applied Mathematics at the University of Manchester, specialising in numerical analysis. She is an associate editor for the SIAM/ASA journal on Uncertainty Quantification and currently co-runs a network called Models to decisions, tackling decision making under uncertainty.

Masoumeh Dashti.
Masoumeh Dashti is a Lecturer in Mathematics at the University of Sussex, working in Bayesian inverse problems.
Marianne Freiberger is Editor of Plus. She interviewed Dashti and Powell in June 2018 after having met them at the LMS Women in Mathematics Day at the Isaac Newton Institute in Cambridge.