
Maths in a minute: Mathematical chaos and the butterfly effect
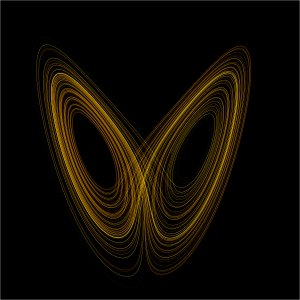
The Lorenz attractor. Image from Wikipedia, reproduced under the Gnu free documentaion license.
Many accounts of chaos theory trace its beginning to an event that occurred in the early 1960s. The American mathematician and meteorologist Edward Lorenz was running computer simulations of basic weather patterns. The simulations were governed by a set of differential equations, and each simulation had to be started off by a set of initial values. One day Lorenz ran the same simulation twice and to his surprise found that the two rounds resulted in completely different weather predictions. He soon found out why: the initial values of the second round had been rounded off by a seemingly insignificant amount. The tiny difference of starting values caused the equations to spit out a completely different set of answers.
What Lorenz had stumbled across became known as the butterfly effect: the tiny air currents caused by a butterfly's wing can amplify to eventually cause a hurricane half-way around the planet. To mathematicians this effect is known as sensitive dependence on initial conditions and it is one of the hallmarks of mathematical chaos. It means that even though your equations can predict the long-term behaviour of your system in theory, in practice they will never be able to do so, since an infinite degree of accuracy would be required to differentiate between initial values that lead to a completely different outcomes.
Lorenz wasn't the first to come across this phenomenon — it had been observed in physical and mathematical systems at least since the beginning of the twentieth century, and some of the maths that lies at the heart of modern chaos theory had been formulated then. But the millions of calculations needed to observe chaotic effects only became possible with the emergence of the computer, and so chaos theory only seriously took off in the second half of the twentieth century.
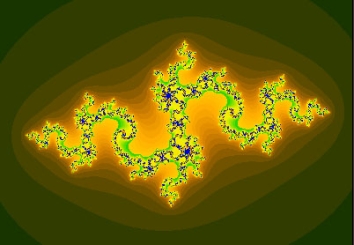
A Julia set, one of the beautiful fractals arising from chaos theory.
Since then mathematicians have given a precise definition of mathematical chaos, with sensitive dependence on initial conditions providing a key concept. They have detected chaos in a wide range of systems modelling physical processes. The humble quadratic equation, used to model population dynamics, has proved to provide chaos in abundance and has served as a guinea pig in mathematicians' attempts to understand this behaviour. They have explored the patterns emerging from chaos and those that give rise to it, and tried to predict its unpredictability. Their insights have impacted on a huge range of areas, from finance to neurology.
No account of chaos theory would be complete without a mention of the beautiful pictures that arise from it. In many cases a dynamical system can be visualised geometrically, for example as the plane or as three-dimensional space. Once you have such a visual model, you can pin-point the regions where chaos arises. Lorenz was one of the first to do this and he came up with the beautifully intricate shape of the Lorenz attractor, which fittingly resembles a butterfly. In the 1970s Benoît Mandelbrot created the first images resulting from systems governed by quadratic equations (find out more here). With the increased availability of computing power, amazing fractal shapes appeared. Their beauty and intricacy rivals those of nature itself and mathematicians knew that they were onto something good. The geometry of chaos, as well as many of its other aspects, is still not completely understood.