Maths in a minute: Ensemble forecasting

Weather forecasts are never 100% certain, as you will see when you look at you weather app. Rather than telling you that it's definitely going to rain or not, it'll tell you a percentage chance. For example, at this very moment my app says the chance of rain today is only 10%.

To see how meteorologists work out these chances, we first need to revisit an old friend, the famous butterfly effect. Meteorologists use mathematical models that can simulate the weather to make their forecasts (you can find out more about these models here). To start off a simulation they need to measure the current values of things like temperature and pressure and feed these to the model. The butterfly effect means that a small inaccuracy in the starting values fed to the model can grow as the model runs through all the calculations necessary to make the forecast. This means that the forecast you get as the output can end up being very inaccurate. Indeed the butterfly effect, also known as sensitive dependence on initial conditions, was first discovered in connection with weather forecasting, find out more here.

Ensemble forecasting is one way of dealing with this problem. Rather than running the weather model just once, meteorologists run it many times, each time with slightly different values for the starting conditions. This gives them a whole ensemble of forecasts. If all these forecasts are very similar, then that means the butterfly effect isn't too pronounced and you can be quite certain the forecasts are accurate. If the forecasts vary widely, then you know that you can't be too certain.

The ensemble of forecasts also gives you the percentage chance you see in your app. If only 10% of the forecasts in the ensemble say that it'll rain, then that's the 10% you see on the app.

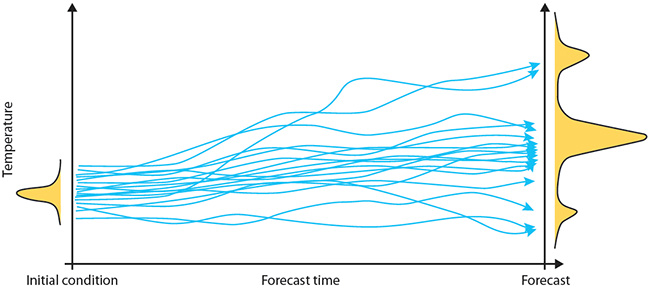
An ensemble of forecasts produces a range of possible scenarios rather than a single predicted value. The distribution of the ensemble members gives an indication of the likelihood of occurrence of those scenarios. Figure from the ECMWF website, CC BY-SA 4.0.

Ensemble forecasting was pioneered by the climate scientist Tim Palmer, and can be used in other situations too, for example when forecasting the behaviour of a pandemic. To find out more listen to Palmer himself talk about ensemble forecasting, uncertainty more generally, as well as climate change in our podcast.

This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.