Randomness is usually something we try to avoid. It's scary and gets in the way of useful outcomes. That's why we spend much of our time engaged in organisational tasks.

It may come as a surprise, therefore, that randomness is a crucial ingredient in artificial intelligence. And even if you don't know much about how AI works, a handy metaphor can show you why.

Moving downhill

The form of artificial intelligence that has seen so much success lately is powered by machine learning models. Such models learn how to perform their tasks by first training on large datasets. For example, a model might be given lots of pictures of cats and dogs. Looking through these images it will spot patterns within their pixels that are linked to cats and patterns that are linked to dogs. Once it has finished learning, the model can then use these patterns to predict (very reliably) whether an image it has never seen before shows a cat or a dog. (You can find out more about machine learning in this article.)

During the training phase, the algorithm initially makes rough guesses of whether an image shows a cat or a dog. It has a way of comparing those guesses to the correct answers and a way of improving itself if they are not good enough. All this is done in the language of mathematics: the difference between predicted answers and correct answers is measured by a mathematical formula called a loss function. The algorithm's task is to make the difference between its guesses and the correct answers as small as possible, in other words, to minimise the loss function.

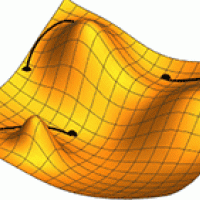
You can think of this metaphorically as moving across a hilly landscape (the loss landscape), looking for the bottom of the deepest valley (the lowest value of the loss function). If you haven't got a map (which an algorithm doesn't) and can't see far ahead (which an algorithm can't), then one way of doing this is to feel the patch of ground around you, identify which direction goes down, move a step in that direction, and then repeat. Machine learning models do the mathematical analogue of this feeling around, it's called gradient descent.

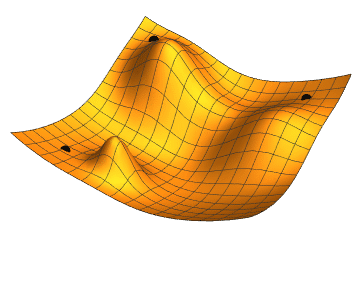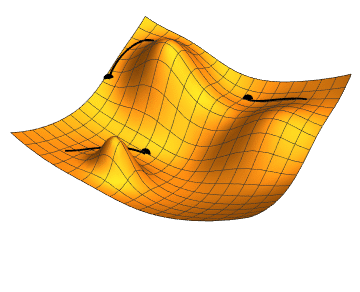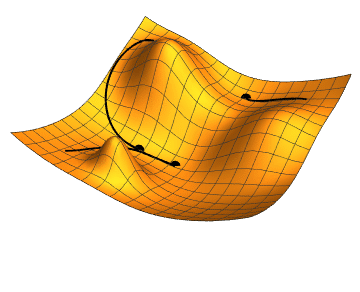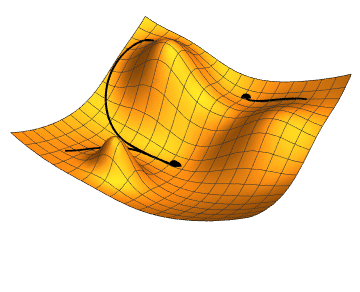
An illustration of gradient descent. Image: Jacopo Bertolotti

The problem with this approach is that you might find yourself stuck at the bottom of a small dip, rather than the deepest valley. You can't get out, as none of the directions around you go down. When this happens to a gradient descent algorithm, then it hasn't found the global minimum of the loss function. It's only found a local minimum. So it hasn't found the lowest value of the loss function. This is what happen to the point at the top right in the animated gif above.

Another problem with the gradient descent method is that, while it's easy for you to feel your way around a little patch of ground, the algorithmic analogue involves performing a calculation involving all the data in the set of training data. Because training data sets are typically huge, this can take a very long time, taking up a lot of computing power. What's more, the calculation needs to be repeated every time a step has been taken, to feel out the new patch of ground.

Introducing randomness

What the algorithm can do instead is perform the feeling around calculation, not using all the data in the training set, but only a smaller collection of it, perhaps only a single data point. To make sure that all data points have a chance of taking part, the algorithm chooses this smaller collection (or single point) at random at each step. This method, called stochastic gradient descent, is not as accurate at finding the minimum of the loss function as ordinary gradient descent, but it can do the calculations much faster.

So far this might not seem too exciting — we've traded accuracy for speed — but there's another neat advantage of stochastic gradient descent. The random choices mean that the path taken through the loss landscape is more random than the path you'd get from non-stochastic gradient descent. It takes steps this way and that, rather than moving more or less directly towards a minimum. But this meandering comes with an advantage. When you're about to get stuck at a local minimum (at the bottom of a small dip), a step in a random direction might just hoist you away (and out of the dip) so that you can continue exploring the landscape to find the true global minimum.

Thus, the introduction of randomness has killed two birds with one stone. It has made things faster and given the algorithm a better chance of getting unstuck. These advantages have contributed to stochastic gradient descent becoming an important workhorse in machine learning. (And while this description has been intuitive and very vague, it can be made mathematically precise.)

Open questions

Machine learning is a rapidly progressing field, where theory often lags behind practice and much is done through trial and error. It's been found, for example, that an extension of stochastic gradient descent, an algorithm called Adam, performs better in the large language models that are behind things like ChatGPT. It's not really clear why that's the case, but it's likely down to the way the algorithms handle the randomness, and how this relates to the structure of the underlying data (words, in the case of a large language model).

Generally, although stochastic gradient descent works really well in many practical applications, theoretical questions about possible effects of its randomness on machine learning models remain unanswered. Indeed, such questions formed the theme of a recent research programme run jointly by one of the UK's leading mathematical research institutions, the Isaac Newton Institute for Mathematical Sciences (INI), and the county's national institute for data science and artificial intelligence, the Alan Turing Institute (ATI).

If randomness tends to make you nervous, we hope that you now feel a little friendlier towards it — and that you agree that machine learning is a fascinating topic!

Abut this article

Jorge González Cázares at the Isaac Newton Institute.

Jorge González Cázares is an Assistant Professor at IIMAS - UNAM in Mexico City. His research includes work in probability, statistics, mathematical finance and machine learning, specialising in Lévy processes, simulation and limit theorems.

González Cázares co-organised the research programme Heavy tails in machine learning Alan Turing Institute in April 2024. It was a satellite programme of the Isaac Newton Institute for Mathematical Sciences.

Marianne Freiberger, Editor of Plus, met González Cázares at the Open for Business event Connecting heavy tails and differential privacy in machine learning organised by the Newton Gateway to Mathematics.

This article was produced as part of our collaborations with the Isaac Newton Institute for Mathematical Sciences (INI) and the Newton Gateway to Mathematics.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. The Newton Gateway is the impact initiative of the INI, which engages with users of mathematics. You can find all the content from the collaboration here.