A group of US researchers has just come up with a mathematical model that gives new insights into why rich and popular people tend to get richer and more popular and why websites that nobody links to tend to remain obscure forever. The new research falls into a field called network theory and it also settles a long-ranging philosophical dispute in this area.

Networks are everywhere.

Networks occur everywhere in the world around us. There are social networks, information networks (formed, for example, by interlinked webpages), technological networks (such as computer or electricity networks), and biological networks (for example those formed by interacting proteins controlling the expression of genes). Understanding the structure of these networks, how they are formed and how they evolve over time, is vital in fields ranging from the social sciences and biology to computer science and engineering.

No matter what kind of network you are thinking about, mathematically speaking, they all boil down to the same thing: a collection of nodes connected to each other by what mathematicians call edges. When researchers started analysing huge real-life networks in the 1990s they found that, irrespective of the situation they arose from, many of these networks exhibited the same feature. Rather than consisting of a majority of average nodes that all have roughly the same number of connections to other nodes, they were dominated by a number of highly-connected hubs.

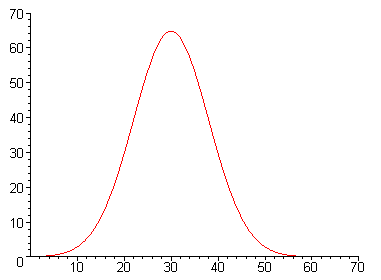
The normal distribution

This phenomenon cropped up in an astonishingly wide range of real-life networks, including social, technological, physical and biological ones, and such networks came to be known as scale-free. Scale-free networks are characterised by the graph of their degree distribution. To plot the graph, you first count the number of connections of each node — this number is called the node's degree — and then plot every possible degree against the number of nodes that have that degree. If the connections were more or less evenly distributed throughout the network, you'd expect the graph to take the familiar bell-shape of the normal distribution, with the average degree, or more properly the mean degree, being the one corresponding to the most nodes and highly or badly-connected nodes being the exception.

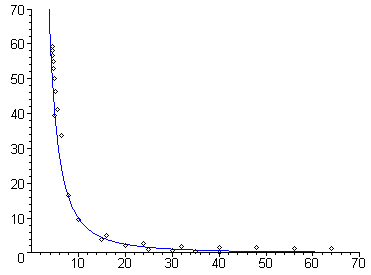
The black circles represent a data set from a typical scale-free network. All points lie on or close to the blue line, which is the graph of a function of the form ax^-k. The degree distribution adheres to a power law.

The graph of a scale-free network, however, adheres to what is called a power law: it approximates the graph of a function of the form f(x)=ax^-k, where a and k are constant. In most real-life examples, k lies somewhere between 1 and 3. In this case there is no peak around the average degree, rather the graph slopes steeply downward as the degree grows: there are a large number of nodes with very few connections dominated by fewer extremely well-connected ones.

But why are so many real-world networks scale-free? In some cases, the answer seems obvious. If you're building a new railway line, for example, it makes sense to connect up with cities that are already well-connected. If you're at a party, you're more likely to get chatting to someone who is clearly sociable, rather than to a loner sitting in a corner. As the network evolves, well-connected nodes become better-connected and badly-connected ones remain badly-connected.

There is a simple way of mathematically simulating this phenomenon, which is called preferential attachment. Start with a network of two nodes and add new nodes one by one. Whenever a new node comes along, it makes a random choice as to which existing nodes to link up with, but the randomness is biased in favour of well-connected nodes: the higher the degree of an existing node n, the higher the probability that a new node will attach itself to n. Networks that evolve according to this mathematical rule adhere to a power law and are remarkably good at simulating real-life networks.

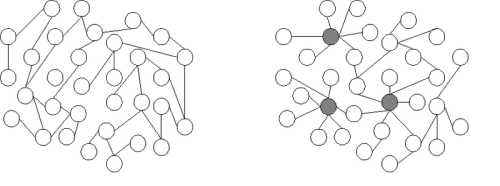
In the network on the left the probability of a new node linking to an existing node is the same for all nodes. Each node here has roughly the same degree. The network on the right is a scale-free network. Here three highly-connected nodes dominate. Image taken from Wikipedia, reproduced under the GNU Free Documentation License.

If you think again, though, you might come to the conclusion that something more subtle must be at work here. It may be advantageous for a new node to connect to well-connected existing nodes, but there are often other factors to take into account — you might want to build your railway line to connect directly to a big city, but if this is too expensive, you go for a medium-sized town. The network theory world thus split into two camps: those who think that preferential attachment should be viewed as the fundamental driving force of network evolution, and those that favour optimisation, in other words a careful balancing of various factors.

And this is where the new work, led by Raissa D'Souza from the University of California, comes in. Her team developed a mathematical model based on optimisation. Whenever a new node comes along, the decision of what existing nodes to link up to is not governed by a probability distribution, but by a cost function which for each existing node calculates the cost of attaching to it. A new node then links up with the existing node that minimises the cost function.

Interestingly, this new model gives rise to preferential attachment. When following through the maths, the researchers found that new nodes are in fact more likely to link up with well-connected existing nodes — that is, up to a point. It turns out that the model naturally evolves a feature often observed in real-life networks and that preferential attachment cannot account for: at some point well-connected nodes become saturated and cannot take anymore links. Simple preferential attachment models are not able to simulate this behaviour, since new nodes gravitate towards well-connected nodes indefinitely in the preferential model.

D'Souza's team tested their model against several real-life data sets, including social, biological, physical and technological networks. In each case they found that the theoretical model was able to simulate these real-life networks remarkably well, in fact better than some preferential attachment models.

The new work is significant both for practical and for philosophical reasons. On the practical level, it may provide the prototype for a class of models that describe real life more accurately than previous ones. In terms of philosophy, the new model shows that preferential attachment can indeed emerge from optimisation processes. This suggests that in real-life processes, the formation of networks is indeed governed by more complicated factors than a simple "go for the most popular" strategy.

Further reading

• You can read the researchers' paper Emergence of tempered preferential attachment from optimization, published in the Proceedings of the National Academy of Sciences of the USA.
• The paper The structure and function of complex networks by M.E.J. Newman gives an excellent overview of the theory of complex networks.
• The Netlogo website has a great applet that evolves networks according to the preferential attachment model.
• You can read more about networks on Plus.