Our theory of very nearly everything: matter and forces
In the last article we saw that light has a lot in common with matter. Despite this, we don't usually refer to light as "matter". In fact, as Faraday realized, light is related to the electromagnetic force. The electric field (which makes like charges repel and opposite charges attract) and the magnetic field (which makes like magnetic poles repel and opposite magnetic poles attract) are in fact parts of a single field, the electromagnetic field, and light consists of waves in this field.

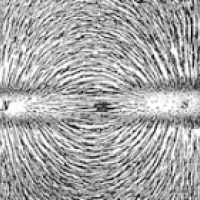
Iron filings scattered around a bar magnet arrange themselves along field lines.
This unified description of light and electromagnetism is extremely successful, and you directly rely on it every time you use a mobile phone or any other wireless gadget. In this description, the electromagnetic field affects, and is affected by, charged particles like the electron. Matter, consisting of particles, interacts with forces, represented by fields.
But how do we square this with the view of light as consisting of photon particles? As we shall see in a moment, quantum field theory provides the answer, and will somewhat blur the line between forces and matter.
Apart from electromagnetism, it has turned out that there are only three other forces in nature: the strong force, the weak force (both terrible names) and gravity. The strong force holds protons and neutrons together in the nucleus, and also the quarks inside those protons and neutrons. The weak force is involved in radioactivity and is the main way stars produce energy. I will keep using electromagnetism as my running example, but the story is similar for the strong and weak forces (gravity is the odd one out).
Quantum fields
If you have read anything at all about modern physics, you will have heard countless testimonies about the incredible strangeness of quantum mechanics, the physics of the very small. This article will be no exception. In fact, taking the principles of quantum mechanics (originally formulated for tiny pointlike particles) and applying them to fields (like the electromagnetic field) makes ordinary quantum mechanics seem like a breeze, and kept even the most brilliant physicists banging their heads against various walls for decades. Luckily for us, their struggles have left us with a marvellous theory, quantum field theory (QFT), which is currently the language of all our physical laws (except gravity). (Professor David Tong has given an excellent public talk about QFT at the Royal Institution; this was part of the inspiration for this article. You can also read more in A brief history of quantum field theory.)
QFT makes sense of our confusion about whether light consists of waves or particles. In very simplified language, the essence is this: quantum mechanics says that waves in a field can't be arbitrarily weak. Instead, you create a large wave by adding together a large number of tiny, indivisible waves. A particle is, more or less, the weakest such allowed wave, as shown in image below.

A particle is the weakest possible wave in a field—the central idea of quantum field theory. (Image: Elias Riedel Gårding)
QFT also explains, in a unified way, many of the science fiction-sounding concepts that are a big part of the allure of physics. For example that some particles have an antimatter partner (just a different type of wave in the same field) and that particles can be created and destroyed, turning into other types of particles (a wave in one field can be transferred into waves in some other field).
The fields of our universe
Let us consider the table of known fundamental particles in the light of quantum field theory. Instead of seventeen fundamental particles, we now have seventeen fundamental fields, for example the electromagnetic field (also called the photon field), the electron field, the up-quark field, the muon neutrino field, the Higgs field, and so on.

The known fundamental particles (Image MissMJ)
Viewing the particles in terms of fields makes it a lot easier to quantitatively describe how the particles behave, by means of an equation (called a Lagrangian, $\mathcal{L}$). For example, to describe the physics of photons, we must first write down the equation governing the electromagnetic field. This equation has long been known to physicists, and it reads
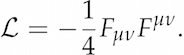
Don't worry about what the symbols in this equation mean; I am just including it to illustrate that this very short equation captures everything we know about electromagnetism and light.
We play a similar game when we want to describe other particles. For example, the equation for the electron field is called the Dirac equation and reads
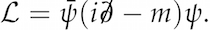
The equations for capturing the behaviour of a particle field are remarkably simple. But you can also bring these together to describe how two types of particles, such as electrons and photons, interact:
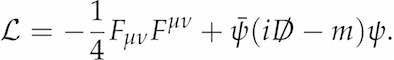
In fact, you can capture all the known interactions between all the known fields in just one, admittedly more complicated, equation:
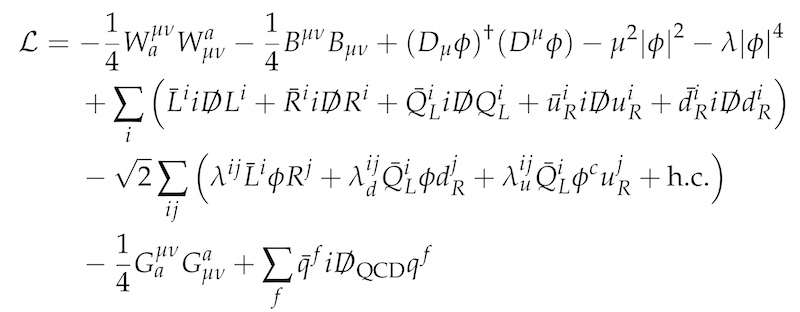
The equation for the standard model. It encodes all known particle interactions.
Defining all the symbols in this equation is a bit messy and might take a few pages, and learning exactly how to interpret them would take you the better part of a year at university or, depending on the level of detail you are aiming for, a research career in physics.
(Suffice it to say that some of the symbols represent the actual fields: $\phi$ is the Higgs field, the $L^i$ and $R^i$ represent the lepton fields, $Q_L^i$, $u_R^j$, $d_R^j$ and $q^f$ all represent the quark fields in various ways, $W^{\mu\nu}_a$ and $B^{\mu\nu}$ represent the electromagnetic (photon) field as well as the $W$ and $Z$ boson fields while $G^{\mu\nu}_a$ represents the gluon field, and that the appearance of the letters $L$ and $R$ refers to left-handed and right-handed particles (in a certain sense spinning clockwise and counterclockwise, respectively) which, in a strange twist, Nature treats very differently from each other.)
But, together with the list of particles in table above, this equation is known as the standard model of particle physics. If you find it daunting, you are not alone. But considering that this single equation captures all the known laws of nature, except – again – gravity, it really isn't all that bad!
Find out how physicists use pictures to do their calculations in the next article.
About the author

Elias Riedel Gårding grew up in Stockholm and chose physics instead of programming for his undergraduate degree because his secondary school physics class was frankly not very good, and he wanted to see what he was missing. He has always been interested in the most basic laws of nature – those of fundamental physics – but it wasn't until his master's degree in theoretical physics that he got to study them properly. He thinks quantum field theory, the basic paradigm of particle physics, deserves to be more widely known, hence this article series.