"A mathematician, like a painter or a poet, is a maker of patterns. If his patterns are more permanent than theirs, it is because they are made with ideas." This much quoted line is from British mathematician G. H. Hardy's famous book, A mathematician's apology, written in 1940. And any mathematician, from the ancient Greeks to those working today, would agree.

Patterns and structures are fundamental to mathematics. They allow mathematicians to spot when something interesting is going on, to identify the core of a problem and to generalise from a specific example to a more general understanding.

Spotting patterns

Can you spot the pattern in this list of numbers?

This is one of the most famous patterns in mathematics: the Fibonacci sequence. It was spotted by Leonardo Pisano, now better known as Fibonacci, in his book Liber Abaci in the thirteenth century. One of the problems he investigated in his book was how fast rabbits could breed in ideal circumstances.

How many will there be in a year?

Suppose a newly-born pair of rabbits, one male, one female, are put in a field. Rabbits are able to mate at the age of one month so that at the end of its second month a female can produce another pair of rabbits. Suppose that our rabbits never die and that the female always produces one new pair (one male, one female) every month from the second month on. The puzzle that Fibonacci posed was... How many pairs will there be in one year?

At the end of the first month, they mate, but there is still only 1 pair.
At the end of the second month the female produces a new pair, so now there are 2 pairs of rabbits.
At the end of the third month, the original female produces a second pair, making 3 pairs in all.
At the end of the fourth month, the original female has produced yet another new pair, the female born two months ago produced her first pair also, making 5 pairs.

Fibonacci quickly realised a pattern was emerging: the number of adult pairs in a given month was the total number of rabbits (both adults and babies) in the previous month

Adults_{nth month} = Rabbits_{(n-1)th month}

and the number of baby pairs in a given month was the number of adult pairs in the previous month

Babies_{nth month} = Adults_{(n-1)th month} = Rabbits_{(n-2)th month} ,

so the total number of pairs of rabbits in a particular month was the sum of the total pairs of rabbits in the previous two months:

Rabbits_{nth month} = Adults_{nth month} + Babies_{nth month} = Rabbits_{(n-1)th month} + Rabbits_{(n-2)th month}.

By spotting this pattern Fibonacci could quickly calculate the answer to his question: after a year there would be 144 pairs of rabbits. Indeed Fibonacci's pattern has emerged in a huge number of places both mathematical and natural – you can find out much more in our article The life and numbers of Fibonacci.

Patterns to structures

The electron diffraction pattern of Zn-Mg-Ho which has a distinctive 5-fold symmetry, identifying the material as a quasicrystal. This discovery resulted in Dan Shechtman winning the 2011 Nobel Prize in Chemistry. (Image by Materialscientist)

Often spotting a pattern in a problem is the first step to understanding the underlying structure involved. And here lies the strength of mathematics: the same mathematical structures can appear in wildly different settings. One common mathematical structure, called a group, arises in almost every area of maths. In the 19th century people were separately studying the symmetry of shapes, trying to solve quintic equations (an equation involving a variable x, where the highest power of x is x⁵), and investigating a deeper understanding of arithmetic. The same structure emerged in all these settings, and has since appeared everywhere from crystallography in chemistry to encoding data on CDs and hard drives.

Group theory is a very well understood area of mathematics and a subject of ongoing research. By identifying this underlying structure in each of these settings, the powerful mathematical machinery that has been developed to understand groups in one setting, can be used to better understand another setting. (You can read more in our package on group theory package.) Revealing the underlying mathematical structure is like the story of the emperor stepping out in his new, non-existent, clothes, it reveals that all these settings are actually examples of the same thing.

Patterns of meaning

People love to spot patterns, it is something that we are intuitively good at. But this sometimes can lead us up the garden path, particularly as we will try to find patterns in anything, even in the random digits of the number π, which will contain each and every pattern of numbers that you could ever think of.

A similarly fruitless search might be in searching for a pattern within the prime numbers. Prime numbers, those whole numbers whose only factors are 1 and themselves, are the building blocks of the numbers. Any whole number can be uniquely written as a product of prime numbers. Mathematicians have been fascinated by the prime numbers for thousands of years, but they still contain many mysteries. There are infinitely many of them, but there is no discernable pattern for how they are sprinkled throughout the other numbers. They can be close together (in fact it is believed there are infinitely many pairs of prime numbers which differ by just 2, these twin primes are as close together as primes can be) or there can be very far apart (in fact there are arbitrarily long gaps between prime numbers).

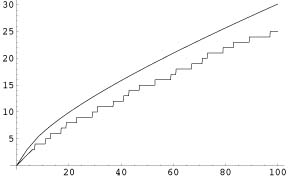
Gauss's function compared to the true number of primes

Finding a pattern in the primes seemed hopeless. They seemed to be scattered randomly along the number line. But a 14-year-old German boy called Carl Friedrich Gauss had a brilliant idea: instead of asking where the primes were, instead ask how many numbers are prime. By asking a slightly different question, Gauss was able to come up with his first estimate: that the number of prime numbers below some number N was about N/ln(N) (where ln(N) is called the natural logarithm of N). This first estimate was good, but Gauss's next estimate was even better, and it worked no matter how far along the number line you looked. (You can read more about primes and Gauss's estimate in The prime number lottery.)

Gauss's idea of counting the primes eventually lead to what is perhaps the hardest open problem in mathematics: the Riemann hypothesis, named after the 19th century mathematician Bernhard Riemann. The mathematics is complex, but essentially in trying to construct an accurate count of the prime numbers, Riemann spotted a pattern in their distribution. (You can read more about the Riemann hypothesis in The music of the primes.) A proof of the Riemann hypothesis would reveal much about the ebb and flow of primes on the number line. Just another example of the power of patterns in mathematics.

About this article

This article was inspired by content on our sister site Wild Maths, which encourages students to explore maths beyond the classroom and designed to nurture mathematical creativity. The site is aimed at 7 to 16 year-olds, but open to all. It provides games, investigations, stories and spaces to explore, where discoveries are to be made. Some have starting points, some a big question and others offer you a free space to investigate.