
The prime number lottery

David Hilbert
On a hot and sultry afternoon in August 1900, David Hilbert rose to address the first International Congress of Mathematicians of the new century in Paris. It was a daunting task for the 38 year-old mathematician from Göttingen in Germany. You could hear the nerves in his voice as he began to talk. Gathered in the Sorbonne were some of the great names of mathematics. Hilbert had been worrying for months about what he should talk on. Surely the first Congress of the new century deserved something rather more exciting than just telling mathematicians about old theorems.
So Hilbert decided to deliver a very daring lecture. He would talk about what we didn't know rather what we had already proved. He challenged the mathematicians of the new century with 23 unsolved problems. He believed that "Problems are the life blood of mathematics". Without problems to spur the mathematician on in his or her journey of discovery, mathematics would stagnate. These 23 problems set the course for the mathematical explorers of the twentieth century. They stood there like a range of mountains for the mathematician to conquer.
As the century came to a close, all the problems had essentially been solved. All except one: the Riemann Hypothesis. The Everest of all Hilbert's problems. It was in fact Hilbert's favourite problem. When asked what would be the first thing he would do if he were brought to life again after 500 years he said "I would ask whether the Riemann Hypothesis has been proved". All indications are that the answer might still be "no" for it appears to be one of the hardest problems on the mathematical books.
As we entered the new millennium mathematicians decided to repeat Hilbert's challenge. In issue 24 of Plus, we saw How maths can make you rich and famous - by solving one of the seven Millennium Prize Problems. The Riemann Hypothesis is the only problem from Hilbert's list that is also on this new list. So read on - this article might be your passport to becoming a millionaire.
The Pattern searcher

One of the great pattern searchers: Leonardo Fibonacci
The Riemann Hypothesis goes to the heart of what it means to be a mathematician: looking for patterns. The search for patterns is perfectly captured by those challenges that invariably come up in the classroom: find the next number.
Here are a list of challenges for you to have a go at. Can you find the patterns and fill in the next numbers?
| 1 | 3 | 6 | 10 | 15 | ? | |||
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | ? | |
| 6 | 19 | 29 | 32 | 34 | 39 | ? | ||
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | ? |

The first two probably presented little problem. The first sequence is known as the triangular numbers. The Nth number in the sequence records the number of stones in a triangle with N rows or in other words, the sum of the first N numbers: 1+2+...+N.

Nature's numbers. Image DHD Photo Gallery
The second sequence is one of Nature's favourite sequences. Called the Fibonacci numbers after the thirteenth century mathematician who first recognized their importance, each number in the sequence is got by adding together the previous two numbers. Invariably the number of petals on a flower is a number in this sequence.

Not so easy to guess. Image DHD Photo Gallery
The third sequence was probably a little more challenging. Indeed, if you were able to predict that 46 was the next number in this sequence, I would recommend you buy a lottery ticket next Saturday. These were the winning lottery numbers on the 22 October 2003.
The last sequence is of course the sequence of prime numbers, the indivisible numbers that can only be divided by themselves and one. It is trying to explain the sequence of prime numbers that the Riemann Hypothesis is all about.
Faced with a sequence of numbers like these, numerous questions spring to the mathematical mind. As well as the challenge of finding the rule to predict the next number, mathematicians are also keen to understand if there is some underlying formula which can help generate these numbers: Is there a way to produce the 100th number on this list without having to calculate the previous 99?
In the case of our sequences, the first two do indeed have formulas that will generate the sequence. For example, to get the 100th triangular number you just have to set $N=100$ in the formula $1/2 \times N \times (N+1)$. A much simpler task than adding up all the numbers from 1 to 100. (A challenge: can you prove why this formula will always work? Here's a hint: take two triangles and build a rectangle with $N+1$ rows and $N$ columns.)
But when you look at the sequence of prime numbers they seem to share more in common with the numbers from the National Lottery. It seems very difficult to predict when the next prime will appear, let alone produce a formula that will tell you that the 100th prime is 541.
Despite the random nature of the primes they have a universal character. The National Lottery numbers have nothing special about them and change from one week to the next. The primes are numbers that have been there for eternity, set into the fabric of the universe. The fact that 541 is prime is a fact that seems stamped into the nature of the Universe. There maybe a different chemistry or biology on the other side of the cosmos but 541 will still be prime. This is why many science fiction writers (for example, Carl Sagan, in his classic novel, Contact, also made into a film of the same name) have chosen primes as the way alien life will communicate with Earth. There is something so special about this sequence of numbers that we couldn't fail to notice the prime number beat if it came pulsating through the cosmos from a distant galaxy.
Aliens may have discovered the primes millions of years ago, but what is the first evidence of humankind listening to the prime number beat? Some people have suggested that the first culture to recognize the primes lived over 8,000 years ago. Archaeologists discovered a bone now called the Ishango bone in Central Equatorial Africa, which has three columns of notches carved down the side. The bone seems to be mathematical in nature. And in one column we find the primes between 10 and 20. But others have argued that these bones are related to keeping track of dates and it is the random nature of the primes which means that a list of dates could well be a list of primes. (You can find out more about the Ishango bone at Ishango: The exhibition.)

The first culture to truly understand the significance of the primes to the whole of mathematics was the Ancient Greeks. They realised that the primes are the building blocks of all numbers. Every number can be built by multiplying together prime numbers. They are the atoms of arithmetic. Every subject has its building blocks: Chemistry has the Periodic Table, a list of 109 elements which build matter; physicists have the fundamental particles which range over weird things as quarks and gluons; biology is seeking to sequence the human genome which is the building kit for life.
But for thousands of years mathematicians have been listening to the primes, the heart beat of mathematics, unable to make sense or to predict when the next beat will come. It seems a subject wired by a powerful caffeine cocktail. It is the ultimate tease for the mathematician: mathematics is a subject of patterns and order and symmetry, yet it is built out of a set of numbers that appears to have no rhyme or reason to them. For two thousand years we have battled to understand how Nature chose the atoms of arithmetic.
There is of course the possibility that, as with the atoms of chemistry, there are only 109 primes which can be used to build all numbers. If that were true, we wouldn't need to worry about looking for patterns to predict primes because we could just make a finite list of them and be done. The great Greek mathematician Euclid scuppered that possibility. In what many regard as the first great theorem of mathematics, Euclid explained why there are infinitely many prime numbers. This proof is described in A whirlpool of numbers from Issue 25 of Plus. Gone, then, is the chance to produce a list containing all the prime numbers like a Periodic Table of primes or prime genome project. Instead we must bring our mathematical tools to bear to try to understand any patterns or structure in this infinite list.
Perhaps the primes start off rather unpredictably and then settle down into a pattern. Let's have a look at the primes around 10,000,000 and see whether here a pattern emerges, whether we might find a formula for predicting the ebb and flow of the primes.
There are 9 primes in the 100 numbers before 10,000,000:
- 9,999,901,
- 9,999,907,
- 9,999,929,
- 9,999,931,
- 9,999,937,
- 9,999,943,
- 9,999,971,
- 9,999,973,
- 9,999,991.
- 10,000,019,
- 10,000,079.
The primes seem to come along like buses: first a great cluster of primes and then you have to wait for ages before the next ones appear. It seems hopeless to find a formula that would spit out this strange list or that would tell us that the 664,571th prime is 9,999,901.

Euclid, who discovered that there are infinitely many primes
Try a little experiment. Take the list of primes around 10,000,000 and try to memorize them. Switch off the computer and see how well you do at reproducing the list. Most of us will try to create some underlying pattern to help us memorize the sequence. Effectively our brains end up trying to store a shorter program that will create the sequence. A good measure of the random character of these numbers is the fact our brains find it hard to construct a program that is significantly shorter than just memorizing the sequence outright.
It's like the difference between listening to a tune and listening to white noise. The inner logic of the tune allows you to whistle it back after a few times, while the white noise gives you no clues as to where to whistle next. The magic of the primes is that, despite first hearing only white noise, a cultural shift into another area of mathematics will reveal an unexpected harmony. This was
Gauss's and Riemann's great insight. Like western ears listening to the music of the east, we will require a different perspective before we understand the pattern responsible for this randomness.
The lateral thinker
What mathematicians are good at is lateral thinking. Professor Enrico Bombieri, a professor in Princeton, expresses what one should do when facing an insurmountable mountain: "When things get too complicated, it sometimes makes sense to stop and wonder: Have I asked the right question?"
It was a fifteen year old boy called Carl Friedrich Gauss who started to change the question. Gauss became an overnight star in the scientific community at the beginning of the nineteenth century thanks to a tiny tumbling rock. The first day of the new century had started auspiciously with the discovery of what many regarded as a new planet between Mars and Jupiter. Christened Ceres, its path was tracked for several weeks when suddenly astronomers lost it as it passed behind the sun. But Gauss was up to the challenge of finding some order in the data that had been collected. He pointed at a region of the sky that astronomers might be expected to see Ceres. Sure enough, there it was.

Carl Friedrich Gauss, 1803
But it wasn't only in the stars that Gauss loved to find order. Numbers were his passion. And of all the numbers that fascinated Gauss, the primes above all were the jewels that he wanted to understand. He had been given a book of logarithms as a child which contained in the back a table of primes. It is somewhat uncanny that the present contained both, because Gauss managed to find a connection between the two.
Gauss decided he would see whether he could count how many primes there were rather than just trying to predict which numbers were prime. Here was the lateral move that would eventually unlock the secret of the primes. He asked: What proportion of numbers are prime numbers? He discovered that primes seemed to get rarer as one counted higher. He made a table recording the changing
proportions.
| N | Number of \\primes from 1 up \\to $N$, often\\ referred to\\as $\Pi(N)$ | On average, how many numbers you need to count before you expect a prime number |
|---|---|---|
| 10 | 4 | 2.5 |
| 100 | 25 | 4.0 |
| 1,000 | 168 | 6.0 |
| 10,000 | 1,229 | 8.1 |
| 100,000 | 9,592 | 10.4 |
| 1,000,000 | 78,498 | 12.7 |
| 10,000,000 | 664,579 | 15.0 |
| 100,000,000 | 5,761,455 | 17.4 |
| 1,000,000,000 | 50,847,534 | 19.7 |
| 10,000,000,000 | 455,052,511 | 22.0 |
So, for example, 1 in 6 numbers around 1,000 are prime.

Since the primes look so random, perhaps tossing a dice might provide a good model of how the primes were distributed. Maybe Nature used a prime number dice to choose primes around 1,000, "PRIME" written on one side and the other five sides blank. To decide if 1,000 was prime, Nature tossed the dice to see if it landed on the "PRIME" side. Of course this is just a heuristic model. A number is prime or it isn't. But Gauss believed that this "prime number dice" might produce a list of numbers with very similar properties to the true list of primes.
How many sides are on the dice as we check the primality of bigger and bigger numbers? For primes around 1,000, Nature appears to have used a six-sided dice; for primes around 10,000,000 one needs a 15-sided-dice. (So there is a 1 in 15 chance that a London telephone number is prime.) Gauss discovered that the tables of logarithms at the beginning of his book containing the tables of primes provided the answer to determining how many sides there are on the prime number dice.
Look again at Gauss's table counting the number of primes. Whenever Gauss multiplied the first column by 10, then the last column, recoding the number of sides on the prime number dice, goes up by adding approximately 2.3 each time. Here was the first evidence of some pattern in the primes. Gauss knew another function which performed the same trick of turning multiplication into addition: the logarithm function.
It was a 17th century Scottish baron, John Napier, who first discovered the power of the logarithm as an important function in mathematics. Napier was generally regarded to be in league with the devil as he strode round his castle with a black crow on his shoulder and a spider in a little cage muttering about the predictions of his apocalyptic algebra. But he is best remembered today for the invention of the logarithm function.
If you input a number $N$ into the logarithm function, it outputs a number $x=\log_{10}(N)$ which solves the following equation: $$ 10^x = N. $$ So, for example, $$ \log_{10}(10)=1; $$ $$ \log_{10}(100)=2; $$ $$ \log_{10}(1,000,000)=6. $$ Whenever I multiply the input by 10 then I add 1 to the output.
But we needn't choose the number 10 to raise to the power x. That's just our obsession with the fact that we have ten fingers. Choosing different numbers gives logarithms to different bases. Gauss's prime number dice function goes up by 2.3 every time I multiply by 10. The logarithm behind this function is to the base of a special number called e=2.718281828459... .
Gauss guessed that the probability that a number N is prime is 1/log(N) where log is taken to the base e. This is the probability that a die with log(N) sides lands on the "PRIME" side. Notice that as N gets bigger, log(N) gets bigger and the chance of landing on the prime side gets smaller. Primes get rarer as we count higher.
If Nature tosses the prime number dice 100,000 times, how many primes will you expect to get with these dice with varying numbers of sides? If the die has a fixed number of sides, say 6, then you expect 100,000/6 which is the probability 1/6 added up 100,000 times. Now Gauss is varying the number of sides on the die at each throw. The resulting number of primes is expected to be $$ 1/\log(2)+1/\log(3)+...+1/\log(100,000).$$
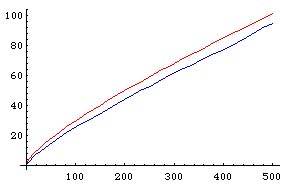
The staircase of the primes versus Gauss's guess Li(N)
Gauss refined this guess at the number of primes into a function called the logarithmic integral, denoted by Li(N). How good is Gauss's guess compared to the real number of primes? We can see the difference in the graph to the left. The red line is Gauss's guess using his prime number dice; the blue one records the real number of primes.
Gauss's guess is not spot-on. But how good is it as we count higher? The best measure of how good it is doing is to record the percentage error: look at the difference between Gauss's prediction for the number of primes and the true number of primes as a percentage of the true number of primes.
| N | Number of primes\\ $\Pi(N)$ from\\1 up to $N$. | How far Gauss's guess\\ Li($N$) overestimates \\ the number of primes \\ less than $N$: \\Li($N$)- $\Pi(N)$ | Percentage error:\\ $\frac{\mbox{Li}(N)-\Pi(N)}{\Pi(N)} \times 100$ |
|---|---|---|---|
| 100 | 25 | 5 | 20 |
| 1,000 | 168 | 10 | 5.95 |
| 10,000 | 1,229 | 17 | 1.38 |
| 100,000 | 9,592 | 38 | 0.396 |
| 1,000,000 | 78,498 | 130 | 0.166 |
| 107 | 664,579 | 339 | 0.051 |
| 108 | 5,761,455 | 754 | 0.0131 |
| 109 | 50,847,534 | 1,701 | 0.00335 |
| 1010 | 455,052,511 | 3,104 | 0.000682 |
| 1011 | 4,118,054,813 | 11,588 | 0.000281 |
| 1012 | 37,607,912,018 | 38,263 | 0.000102 |
| 1013 | 346,065,536,839 | 108,971 | 0.0000299 |
| 1014 | 3,204,941,750,802 | 314,890 | 0.00000983 |
| 1015 | 29,844,570,422,669 | 1,052,619 | 0.00000353 |
| 1016 | 279,238,341,033,925 | 3,214,632 | 0.00000115 |
Gauss believed that as we counted higher and higher the percentage error would get smaller and smaller. He didn't believe there were any nasty surprises waiting for us. His belief became known as:
Gauss's Prime Number Conjecture: The percentage error gets smaller and smaller the further you count.
There is a lot of evidence here, but how can we really be sure that nothing weird happens for very large N?
In 1896 Charles de la Vallée-Poussin, a Belgian, and Jacques Hadamard, a Frenchman, proved that Gauss was correct. But here is a warning that it is far from obvious that patterns will persist. Gauss also thought that his guess would always overestimate the number of primes. The evidence from the tables looks overwhelming. But in 1912 Littlewood, a mathematician in Cambridge, proved Gauss was wrong. However the first time that Gauss's guess underestimates the primes is for N bigger than the number of atoms in the observable universe - not a fact that experiment will ever reveal.

Georg Friedrich Bernhard Riemann
Gauss had discovered the "Prime Number Dice" used by Nature to choose the primes. They were dice whose number of sides increased as larger and larger primes are chosen. The number of sides grew like the logarithm function. The problem now was to determine how this dice landed. Just as a coin rarely lands exactly half heads and half tails, Gauss still didn't know exactly how this dice was landing.
It was Gauss's student Riemann who discovered that music gave the best explanation of how to get from the graph showing Gauss's guess to the true graph of the number of primes. As we shall discover in next issue's instalment, Riemann's music could explain how Nature's dice really landed.
About the author

Professor Marcus du Sautoy is an Arsenal fan. His favourite primes are featured on the cover of his book The music of the primes (reviewed in last issue of Plus).
Comments
Anonymous
Professor Marcus du Sautoy :
I am a Chinese student,
I am reading your book ----- ---- translated into chinese
is very nice,and I am reading the book of wrote by John Ddebyshire,
PRIME OBSESSION is easy to understand ,but your book is more widely and deeply in prime,I cound feel you love the
mathsmatic so much and understand mathsmatic intelligence.
but how to get the 1/2+14.174725i etc?
can you give me some web site about how to get the 1/2+14.174725i ?
Anonymous
The Croft Spiral Sieve, a very efficient multiplicative sieving algorithm derived from the set of all numbers not divisible by 2, 3, & 5, reveals the perfectly symmetrical deterministic process, employing 8 progressively expanding "chord" patterns, whereby the final post-factorization result is all primes >5 up to a given n: www.primesdemystified.com
Anonymous
This was said to be unsolvable by a no less eminent scientist than G.B. F. Riemann. However, if ordered sets of the prime sequence are set out as another sequence:
[3, 5, 7, - 15], [5, 7, 11, - 23], [7, 11, 13, - 31], ... and these sets are treated as points in a four dimensional hyperspace, then the sequence becomes a polygonal arc in 4D. Using linear algebra, finding the direction ratios and intercepts of the line segments produced of the arc, starting from the first two points provides a means of lowering the dimension of the space by unity at a time, but with no loss of information about the prime sequence. This is because on the axis planes, where intercepts are located, one of the co-ordinates is zero and the other remaining co-ordinates become a point in a space of dimension, one less. Finally in 2D space, the intercepts of finite discrete functions of the gradients or higher derivatives might have regularity, or a way of producing regularity might be found. This exercise can be done in any even dimension hyperspace: [4, 6, 8, ... ]
There are four co-ordinates here because of a constraint, that is the sum of an even number of uneven integers is an even integer [zero included]. The solution to the subject appears to reduce to an exercise in linear algebra and a discrete version of the Legendre transformation.
Anonymous
Further to my comment that the sequence of primes can be thought of as a series of points that are solutions to an equation such as [p[1] + p[2] + p[3] - [p[1] + p[2] + p[3]] = 0, where the co-ordinates are: [p[1], p[2], p[3], - [p[1] + p[2] + p[3]] forming a polygonal arc in a hyperspace of even dimension: [2, 4, 6, 8, ... ], four in this case, the problem being treated as an exercise in linear algebra [the dimension 2D case is degenerate] and a discrete version of the Legendre Transformation, since there is no loss of information in lowering the dimension, it should be possible to reconstruct the 4D, 6D, ... arc from discrete 2D finite functions, derived from the hyperspace in the first instance. If the 2D functions of intercept vs gradient or higher derivatives are regular, then these 2D functions can be augmented and then reconstructed in the hyperspace so allowing more points in the hyperspace to be found and hence more prime numbers computed. In the case of a 6D space, the sequence would read: [3, 5, 7, 11, 13, - 39], [5, 7, 11, 13, 17, - 53] , ... Additionally, the fact that uneven integers differ by a multiple of two and the two categories: [4k + 1] and [4.k + 3] can be built into the maths. I do not know that this approach has ever been used elsewhere.
Anonymous
I have already commented on how the above problem could be solved using the linear algebra of a hyperspace of even dimension and a discrete version of the Legendre Transformation involving higher derivatives of the intercept with respect to the gradient in 2D space by the process of a descent to the lower dimension and ascent to the higher dimension without loss of information. It is almost self evident that a successor prime must depend exclusively on its antecedents. [the number two [2] is in an excluded class of its own, itself].
The difficulty I have with the Riemann zeros is that I do not understand their significance in relationship to the sequence: [3, 5, 7, 11, ... ]. Perhaps if the Riemann zeros were computed in a for series where every even number was suppressed, then this would clarify matters.
I have an e-mail address, if someone wants to communicate with me on the matter of hyperspaces, Legendre Transformations and dimension reductions. This is: wpgshaw@hotmail.com
Anonymous
An inspired guess about how Hilbert chose the subject of his famous lecture of 1900! In fact, by then Hilbert's reputation was matched only by that of Henry Poincaré among his contemporaries, and that is why he was chosen by his colleagues to address the momentous topic of that lecture.
Anonymous
Unfortunately prime count with Li(x) and even R(x) Riemann zêta function make a very roughly count of prime with large counting deviation.
Here is a new table count for curious:
Table du décompte des nombres premiers avec Go(X) et les écarts de calcul par rapport à pi(x).
X Go(x) pi(x) -Go(x) @
1,E+01 3,9 0,1
1,E+02 24,6 0,4
1,E+03 167,7 0,3
1,E+04 1 228,4 0,6
1,E+05 9 592,6 -0,6
1,E+06 78 498,6 -0,6
1,E+07 664 578,1 0,9
1,E+08 5 761 454,3 0,7
1,E+09 50 847 534,5 -0,5
1,E+10 455 052 511,9 -0,9
1,E+11 4 118 054 813,4 -0,4
1,E+12 37 607 912 018,1 -0,1
1,E+13 346 065 536 838,3 0,7
1,E+14 3 204 941 750 802,4 -0,4
1,E+15 29 844 570 422 668,4 0,6
@ gaston ouellet
This generalized count is realized with ( X2^2 - X1^2) / ln( X2^2). Fanstastic.