
Perfect buildings: the maths of modern architecture
Architecture has in the past done great things for geometry. Together with the need to measure the land they lived on, it was people's need to build their buildings that caused them to first investigate the theory of form and shape. But today, 4500 years after the great pyramids were built in Egypt, what can mathematics do for architecture? At last year's Bridges conference, which explored the connections between maths and art and design, Plus met up with two architects of the Foster + Partners Specialist Modelling Group, Brady Peters and Xavier De Kestelier, to cast a mathematical eye over their work.

The London City Hall on the river Thames. Note the giant helical
stair case inside. Image © Foster + Partners.
Foster + Partners is an internationally renowned studio for architecture led by Norman Foster and a group of senior partners. It has created landmarks like 30 St Mary Axe in London (also known as the Gherkin), London City Hall and the Great Court at the British Museum. Ongoing projects include one of the biggest construction projects on the planet, Beijing International Airport, as well as the courtyard of the Smithsonian Institution in Washington DC and the new Wembley Stadium in London.
Many of Foster + Partners' projects have one thing in common: they are huge. This means maximal impact on their environment and its people. Designing such enormities is a delicate balancing act. A building not only needs to be structurally sound and aesthetically pleasing, it also has to comply with planning regulations, bow to budget constraints, optimally fit its purpose and maximise energy efficiency. The design process boils down to a complex optimisation problem. It's in the way this problem is solved that modern architecture differs most from that of the ancient Egyptians: advanced digital tools can analyse and integrate the bewildering array of constraints to find optimal solutions. Maths describes the shapes of the structures to be built, the physical features that have to be understood and, as the language of computers, forms the basis for every step of the modelling process.
The Specialist Modelling Group
The Foster + Partners Specialist Modelling Group (SMG), of which De Kestelier and Peters are members, was set up in 1997. The SMG's job is to help architects create virtual models of their project. "Usually a team come to us with a concept," says De Kestelier, "that could be anything from a sketch to something already quite developed. We then help them to model it using CAD (computer aided design) tools, or we develop tools for them."

Mathematical surfaces populated with panels. Image courtesy Brady Peters.
With the help of computers you can model pretty much every aspect of a building, from its physics to its appearance. Computer models can simulate the way the wind blows around the building or sound waves bounce around inside it. Graphic programs can explore different mathematical surfaces and populate them with panels of different textures. And all the information you get from these models can be pulled together in what is probably the most important innovation in architectural CAD tools in recent years: parametric modelling.
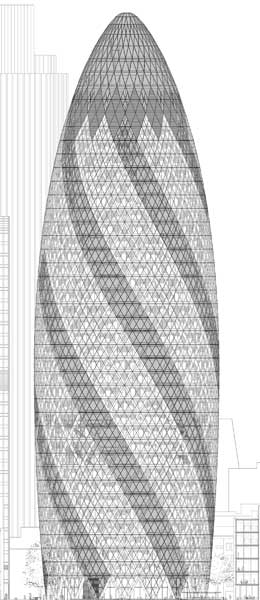
An architect's model of 30 St Mary Axe. Image © Foster + Partners.
Parametric modelling has been around since the 1960s, but only now are architects fully exploiting its power. The models allow you to play around with certain features of a building without having to re-calculate all the other features that are affected by the changes you make. This makes them extremely powerful design tools. Take the Gherkin shown on the left as an example. If you decided to make the building slightly slimmer, this would have a knock-on effect on some other features. You'd have to re-calculate its out-lining curves and the angles of its diamond shapes, for example. This is quite a lot of work and even when it's done, you'd still have to draw a new sketch, either by hand or by re-programming your computer.
Parametric models do all this for you. They allow you to change a variety of geometrical features while keeping fixed those features you have decided should not change. The models function a bit like spreadsheets: changing a feature of the building is like changing an entry of the spreadsheet. In response to a change the software regenerates the model so that pre-determined relationships are maintained, just like a spreadsheet re-calculates all of its entries.
Equipped with the digital tools provided by the SMG, a design team can explore a huge range of design options in a very short period of time. The team can change geometric features of a building and see how the change affects, say, aerodynamic or acoustic properties. They can explore how complex shapes that are hard to build can be broken down into simpler ones, and they can quickly calculate how much material is needed to estimate the cost. The results are buildings that would have been impossible only a few decades ago, both because their complex shapes were next to impossible to construct and because of the degree to which they exploit science to interact optimally with their environment.
The Gherkin
The Gherkin is one of the projects the SMG was involved with and is a prime example of how geometry was chosen to satisfy constraints. Going by the official name of 30 St Mary Axe, the building is 180 metres tall, three times the height of the Niagara Falls. There are three main features that make it stand out from most other sky-scrapers: it's round rather than square, it bulges in the middle and tapers to a thin end towards the top, and it's based on a spiralling design. All these could easily be taken as purely aesthetic features, yet they all cater to specific constraints.
A major problem with buildings of the Gherkin's size is that air currents sweeping around them create whirlwinds at their base, making their immediate vicinity an uncomfortable place to be. To address this problem, the SMG advised the architects to use computer models which, based on the mathematics of turbulence, simulate a building's aerodynamic properties. The model showed that a cylindrical shape responds better to air currents than a square one and reduces whirlwinds. The fact that the tower bulges out in the middle, reaching its maximal diameter at the 16th floor, also helps to minimise winds at its slimmer base.
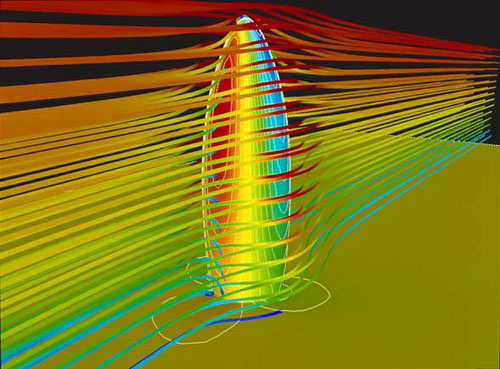
A model of air currents flowing around the Gherkin. Image © Foster + Partners.
But even if you're not being ruffled by strong winds, standing next to a sky-scraper can be eery. It dwarfs you, it eclipses shorter buildings and it takes away the sunlight. Again, it's the Gherkin's distinctive shape that helps minimise these effects. Its bulging middle and its tapered top ensure that you never see its top from below, thus not making you feel quite as small. And the Sun and other views still have a chance to peep through to the bottom.
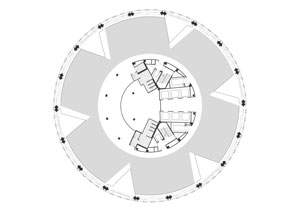
The Gherkin's floor plan. Image © Foster + Partners.
One thing that was decided at the outset was that the Gherkin should be as sustainable a building as possible, and this meant choosing a shape that maximises natural air ventilation (to save on air-conditioning) and the influx of natural sunlight (to save on heating and lighting bills). Six triangular wedges were cut out of the circular plan of each floor, penetrating deep into the building's interior. These serve as light wells, and the shafts they create increase natural ventilation. However, the wedges do not sit right on top of each other. Aerodynamic modelling showed that ventilation is maximised if the plan of one floor is rotated by several degrees with respect to the one below. Thus, the shafts the wedges create spiral up the building and interact optimally with the air currents caused by the building's outward shape. Windows in the facade of the wedges open automatically and draw fresh air into the building. As a result of this carefully chosen geometry, the building reportedly uses 50% less energy than others of comparable size.

The inside of the Gherkin. Triangular wedges have been cut out of its floor plan. They serve as light wells and increase air circulation. Image © Foster + Partners.
The London City Hall
The London City Hall houses the Mayor of London, the London Assembly and the Greater London Authority. The use of glass and a giant helical staircase in the interior are supposed to symbolise the transparency and the accessibility of the democratic process. What is most striking when looking from the outside, though, is the building's odd shape.

The London City Hall on the river Thames.
Perched on the banks of the river Thames, the building is reminiscent of a river pebble, with its roundness again hinting at the democratic ideal. But as with the Gherkin, the shape was not only chosen for its looks, but also to maximise energy efficiency. One way of doing this is to minimise the surface area of the building, so that unwanted heat loss or gain can be prevented. As the mathematicians amongst you will know, of all solid shapes, the sphere has the least surface area compared to volume. This is why the London City Hall has a near-spherical shape.
The building's lopsidedness is also conducive to energy efficiency: the overhang on the South side ensures that windows here are shaded by the floor above, thus reducing the need for cooling in the summer. As with the Gherkin, computer modelling showed how air currents move through the building and the geometry within the building was chosen to maximise natural ventilation. In fact, the building does not require any cooling at all and reportedly uses only a quarter of the energy of comparable office spaces.
Even the helical staircase was not chosen for entirely aesthetic reasons. As part of their analysis, the SMG modelled the lobby's acoustics, quite appropriately for a building representing the voice of the people. Initially the acoustics were terrible with echoes bouncing around the large hall. Something was needed to break up the space. One of Foster + Partners' past projects provided a clue: the Reichstag in Berlin also contains a large hall, but in this case it is broken up by a large spiral ramp. The SMG created a model of a similar spiral staircase for the London City Hall and the company Arup Acoustics analysed the acoustics for this new model. As you can see in the animation below, sound is trapped behind the staircase and echoes are reduced, so the idea was adopted in the final design. (Animation © Arup Acoustics.)
The geometry

A view of the Gherkin. Note the flat panels approximating
a curved shape. Image © Foster + Partners.
What makes the Gherkin, the London City Hall and many other Foster + Partners' structures look so modern is the fact that their outer skins are made up of curved surfaces. These are notoriously difficult and hence expensive to produce, so here's a geometer's challenge: how do you best construct them from simpler shapes?
"This is one of our main challenges," says De Kestelier, "in fact 99% of our projects don't contain any curved surfaces at all. [The Gherkin], for example, only has a single curved panel and that's the lens right at the top." The impression of the building being curved is created by approximating the curved surface by a number of flat polygonal panels — the more panels the truer the illusion.
The SMG have become experts at finding such flat panel solutions to describe complicated surfaces. And, as De Kestelier explains, the geometry is often determined by economy: "We tend to use quadilateral panels, because that's more economical. It's cheaper when you cut the material. With triangles you lose quite a lot of material, but not with quadilaterals. It's also nicer visually I think, because with quadilaterals you see less structure." This is illustrated in the London City Hall whose surface consists entirely of quadilateral shapes.
In fact, the London City Hall illustrates beautifully the need to strike a balance between ideal geometrical shapes and buildability: its awkward bulbous shape was dealt with by cutting it into slices. Each of them is a slice of a slightly tilted cone, which can easily be described mathematically and is easy to approximate by flat panels.
Rational design
Surfaces that can be described by mathematical equations — such as slices of cones, tori, or spheres — often form the basis of the SMG's design. This is advantageous when it comes to creating virtual models, as mathematically generated surfaces are easily represented on a computer. Rather than describing a structure by a large number of individually stored co-ordinates, you only need to store an equation. The exact shape of the surface can be controlled by varying the parameters in the equation (see the figure below for an example). Flat panel solutions can then also be modelled with relative ease: the software simply has to draw straight line segments between a collection of node points on the original surface.
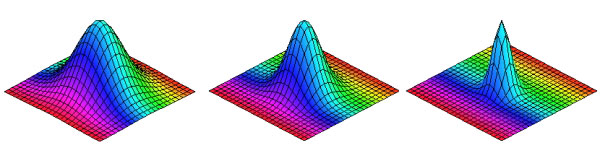
These surface are the graphs of the function z=e-a(x2+y2). Here the 3-dimensional co-ordinate system is formed by the x, y and z axes, with z being the vertical axis. The number a determines the shape of the surface. The first surface has a=1, the second a=5 and the third has a=7.
Thinking of a complex structure as a collection of mathematically defined components is not just useful in the virtual world: it helps turn a model of a building into a step-by-step guide on how to actually construct it. This process of rationalisation forms another important part of the SMG's work. But, as before, mathematical perfection has to make way for practicality: "The other week someone came to me with the plan of a wall that was part of an ellipse," says De Kestelier. "Of course an ellipse is easy to describe mathematically, why would you want to rationalise it further? Well, I decided to rationalise this piece of ellipse into three circular arcs. The reason is, when the wall is being built, you need to cast a concrete wall. This is done using a number of casting panels that fit together to give the overall shape. If you have an ellipse, all your casting panels have to be different: the curvature of an ellipse changes constantly as you go around it. If instead of an ellipse you have three arcs, then you only need three sets of panels and the panels in each set are the same. This is much easier." What is ideal for a mathematician is not always ideal for an architect.

The roof of the British Museum in London, designed by Foster + Partners.
Polymaths
So the SMG use computer programming to model both the appearance of a building and physical phenomena like aerodynamics and acoustics. Their understanding of geometry feeds directly into the design and the construction process. Are they experts in the mathematical sciences, rather than architects? It turns out that seven of the eight SMG members are architects by trade, although they do have specialised expertise ranging from complex geometry and environmental simulation to parametric design and computer programming. The eighth member of the group is an engineer and acts as the main programmer.
When it comes to modelling physical features based on complicated maths, the team often use specialist consultants. "We do do preliminary analyses within the team, but if we need to know more, we go elsewhere. We act as the point of contact between the specialised consultants and the designers," Peters explains. And what about the pure maths, the geometry? How complicated is that? "We have one A level book in the office, and that's it," says De Kestelier. After all, it's all about creating buildable structures, so anything that goes beyond classical geometry is out of place here.
While maths is inherent in most of the SMG's activities, both Peters and De Kestelier insist that their understanding of design is what qualifies them for the job. "The important thing to realise is that we are architects that do programming, not programmers that work in architecture," says De Kestelier. Peters agrees: "One of the major things we do is not the modelling," he says. "It is to understand what the parameters of a project are and to break them down into definable rules. We help understand where the flexibilities are and where the constraints are." Optimising constraints and creating buildable objects is, of course, what architects have always done and De Kestelier and Peters both think that in essence the job of an architect hasn't changed. It's just that, thanks to modern digital tools, architects today can explore a range of design options that previous generations could only dream of. As the language of form and pattern, of science and computers, it's maths that has put these tools at their disposal — it has certainly paid back its due.
About this article
Marianne Freiberger is co-editor of Plus.

Xavier De Kestelier (on the left) and Brady Peters (on the right) are member of the Foster + Partners Specialist Modelling Group.
Plus met Brady and Xavier at the 2006 Bridges conference on mathematics and art, which took place in London. Details on the Bridges conference series can be found on its website.
This content now forms part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from our collaboration here. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Anonymous
should your equation be z=e^(-a(x2+y2)), not z=e^(-a(x2-y2))?
Marianne
Yes you are right, thanks for pointing out the mistake. We've fixed it.
Anonymous
Could you please indicate which software(s) Foster + Partners Specialist Modelling Group has used or maybe recommends? Thanks!!