Phillip Griffiths: Beauty, truth and being practical

Phillip Griffiths.

"I love Phillip Griffiths' books. Every time I read one I want to go and hug the guy." That's rare praise for maths textbooks, bestowed on Griffiths by a mathematician I met during coffee at the International Congress of Mathematicians in Seoul. Griffiths came up in our chat because he had just been awarded the Chern medal which bestows the "highest level of recognition for outstanding achievements in the field of mathematics". These include Griffiths' mathematical work, but also his books, his work for maths education and for the mathematical community as a whole.

Beauty and truth

Listening to Griffiths talk about maths you get a clear sense of what draws him to it. He quotes the mathematician Herman Weyl: "My work always tried to unite the truth with the beautiful but when I had to choose one or the other, I usually chose the beautiful". Because, as Griffiths points out, the beautiful often turns out to be true in a deeper way.

It's a side of mathematics that is often hidden from the outside view. What we see in school books are stern formulas and rigid logic — no room for choice, let alone personal preference. But those textbooks only present the final results, pulled like a rabbit out of a hat. The course of mathematics, whether historical or in the work of a single person, is way more meandering and haphazard than that rabbit suggests. When you are wandering the wilderness of the unknown, discovering (or inventing) new maths, you need something to guide you, and often that something is a sense of aesthetics. "You find out what the most harmonious properties of a [mathematical] structure are, the most aesthetically pleasing way to see it, and then you let that guide you," says Griffiths.

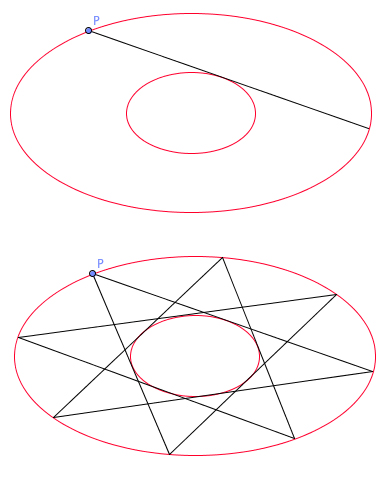
Poncelet's ellipses.

Griffiths takes delight in those twists and turns of mathematical history. When he started out in maths there were no textbooks covering the area he worked in, so he had to go back to the old masters. Reformulating their work and bringing it up to modern standards of rigour is in part what he is being honoured for. He told me how his own area of maths took one starting point around 1812 in a Russian jail. Here Jean Victor Poncelet, a French engineer and mathematician captured during Napoleon's campaign against the Russian Empire, gave some serious thought to geometry.

Poncelet was thinking about problems such as this one. Suppose you have two ellipses, one sitting within the other. Pick a point P on the outer ellipse and draw a straight line that just touches (is tangent to) the inner ellipse. Extend that line until it hits the outer ellipse again and repeat the process. It's conceivable that after drawing a few of these tangent lines, you end up at the point P you started at. Naively, you would think that this periodic behaviour is pretty rare; that it only happens for some very special starting points P. But Poncelet proved a surprising result: if such periodic behaviour occurs for one starting point P, then it occurs for all starting points on the outer ellipse. So, depending on the ellipses, this billiard-like game is periodic everywhere, or nowhere.

It's all connected

This type of problem seems worthy of an engineer, but also rather isolated. Yet it turned out that Poncelet's result is closely related to a ground breaking one, proved a few years later in 1822, by the twenty-year-old prodigy Niels Henrik Abel. Building on work of many notable mathematicians Abel was trying to evaluate objects called elliptic integrals. These cropped up in a number of contexts. For example, you needed to evaluate elliptic integrals to figure out the length of an arc of an ellipse, and also in mechanics, for example to describe the motion of a pendulum. (Elliptic integrals are special cases of the more general integrals of algebraic functions.)

With these kind of problems you hope for a general formula that gives you the solution. For example, the length $L$ of an arc of a circle is $L = r\theta,$ where $r$ is the radius of the circle and $\theta$ is the angle at the centre of the circle that defines the arc (see the figure below). For elliptic integrals (and also for the integrals of most algebraic functions more generally) no such formulas existed. "What you got by integrating algebraic functions was a very mysterious quantity," explains Griffiths. "You cannot evaluate it by anything that is in closed form," that is, by any neat formula. With his deep insight into the inner symmetries of such integrals, Abel realised that while you could not easily evaluate them, you could decompose them into components that are much easier to deal with: they can be expressed using elementary functions mathematicians were familiar with.

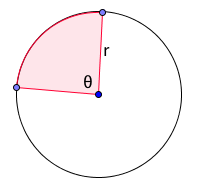
The length of the red arc of the circle is θr.

Surprising though it may seem, Abel's result and Poncelet's result on bouncing around between ellipses were both manifestations of the same underlying mathematics. Neither Poncelet or Abel were aware of this link and they never had the pleasure of meeting. Abel's work found no immediate recognition and he died a few years later, in 1829, from tuberculosis and in poverty.

Geometry via algebra

Abel's result was a breakthrough, and it marked the birth of Hodge theory, Griffiths' favourite area of maths. Ellipses and circles are geometric shapes, but they can be described using algebra (see the box on the right). In a similar vein, you can study other geometric shapes that are defined by certain algebraic equations. These can be curves such as hyperbolas or parabolas, they can be surfaces such as spheres, and they can even be higher dimensional shapes you cannot visualise. The good thing about such algebraic varieties, as they are called, is that you can use the poweful tools of algebra to understand them, even if you can't picture them.

Hodge theory is about understanding the geometry of complicated algebraic varieties using information encoded in a much simpler algebraic structure, called the Hodge structure of an algebraic variety. It's on these Hodge structures Griffiths has worked on most of his life, making major contributions to the area. But there is still much work to be done. One open question, called the Hodge conjecture, was designated in 2000 as one of the seven most difficult problems in maths by the Clay Mathematics Institute. Very loosely speaking, the conjecture concerns the question whether every component in the Hodge structure of an algebraic variety also has an algebro-geometric interpretation.

The Clay Mathematics Institute is offering $1 million for a resolution of the Hodge conjecture, but so far no one has been able to claim it. "It's one of these problems that probably requires some deeper level of understanding," says Griffiths. "It's not a problem you can just work on directly at the moment. My guess is that it's going to be [solved using] some combination of ways of looking at it from different perspectives, put together in a way nobody has thought of before." But as Griffiths also points out, there is always the chance that a lone engineer in jail, or perhaps a twenty-year-old genius, comes up with the magic ingredient that clinches the prize.

When it comes to teaching such complex mathematics, Griffiths isn't a stickler for formalism. He tends towards teaching students how to think about a problem, he says, rather than how to actually do it (though he notes the latter is important too). And he expresses admiration for the mathematician Solomon Lefschetz, who reportedly never stated a false result nor wrote down a completely correct proof (according to the prevailing current standards). It's about gaining a deep sense of a problem, rather than getting all the formalities right straight away. Griffiths' teaching technique seems to work. He has had 29 PhD students many of whom had glittering careers, producing a total of 460 "doctoral descendents".

But he is also interested in how mathematics is taught to people who won't go on to become mathematicians, but will need mathematics in one form or another in their jobs. In this context Griffiths is down to Earth. That kind of teaching should be "demand driven" he says: don't teach the maths in isolation, but also teach people how they are going to use it in their jobs and lives.

Being practical

Phillip Griffiths being awarded the Chern medal by the President of South Korea, Park Geun-hye. Image ⓒ 2010-2014 International Congress of Mathematicians 2014, all rights reserved.

Griffiths' influence goes way beyond personal contacts. In various roles he has shaped science policy, from maths and science education back home in the US to forming the Science Initiative Group, which is dedicated to fostering science in developing nations. Between 1991 and 2003 Griffiths was director of the Institute for Advanced Study in Princeton, one of the best research centres in world. According to the International Mathematical Union, the body that awards the Chern medal, Griffiths has had "a substantial impact on the entire scientific enterprise the world over". (For a comprehensive review of all of Griffiths' achievements, which we haven't got space to list here, see this summary produced by the International Mathematical Union.)

Now aged 76 Griffiths has left behind the "wilderness of administration" as he calls it, and is devoting most of his time to the maths. Receiving the Chern Medal is "the most moving experience" of his professional life he says. It's got a very special significance for him: Shiing-shen Chern, after whom it is named, was Griffiths' mentor, collaborator and friend. With all of Griffiths' achievements the medal couldn't be more deserved.

About this article

Marianne Freiberger is Editor of Plus. She interviewed Phillip Griffiths at the International Congress of Mathematicians in Seoul in August 2014.