The power of good questions

What makes a good maths question? If you are a student facing exams, you might (understandably) say that good means easy. But if you're doing maths for fun, or are a professional mathematician, your answer is going to be different. An easy question is boring, but you also wouldn't want to gnaw your teeth out at something that is completely inaccessible. What mathematicians like most are questions that lead to new insights, to new ways of looking at things, or pose a completely new type of problem. Asking "good" questions is an important part of doing maths. But where do these good questions come from?

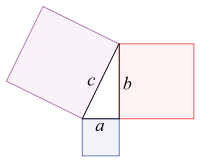
Pythagoras' theorem. Image: Wapkaplet.

Generalise

One source is generalisation. A great example of this is a question posed over 350 years ago by the French mathematician Pierre de Fermat, and has become known as Fermat’s last theorem. As we know from Pythagoras’ theorem, if $a$ , $b$ and $c$ are the sides of a right-angled triangle, with $a$ and $b$ enclosing the right angle, then

$a^2+b^2=c^2.$

Fermat asked himself what happens if you make this equation more general: instead of squaring the numbers, you raise them to some other power $n$ with $n>2.$ Can you find three positive whole numbers $a$ , $b$ , and $c$ so that

$a^ n+b^ n = c^ n?$

Fermat's question seems pretty straight-forward, but it took mathematicians over 350 years to prove that the answer is no. In the process they developed a whole new area of mathematics; a new range of mathematical tools. In fact, it turns out that Fermat's last theorem is a special case of a much broader and deeper problem which involves a particular type of geometric curve that on the face of it has little to do with the original question. So Fermat's simple question turned out to be incredibly fruitful: it generated new mathematics, new insights and new ways of looking at things. Though hard, many mathematicians would regard this as a "good" question. (You can find out more about Fermat's last theorem here).

Simplify and vary

A question is also promising if it offers lots of room for variation. You then start on the simplest variant and see if you can proceed from there, hoping that something interesting will come along as you do so.

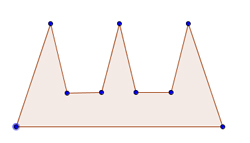
How many guards do you need to supervise a gallery with this floor plan?

A nice example is the art gallery problem: how many security guards do you need to be sure that together they can oversee the whole interior of an art gallery?

This question is inviting because you can easily draw pictures of the floor plan of a gallery and guards stationed within it. To start with, you will probably think of art galleries that have a relatively simple shape. The first answer, given in 1978 five years after the problem was posed, worked for galleries whose floor plan has the shape of a simple polygon: a shape bounded by straight line pieces that do not cross. Guards were placed in the polygon's corners and were not allowed to move around. Using an ingenious line of attack, the mathematician S. Fisk proved that you never need more that n/3 guards, where n is the number of vertices (corners) of the polygon. (See this article for more.)

Now there are several ways of making the problem harder. What if the guards are not confined to the corners of the gallery? What if they are allowed to move around? What if there are obstacles in the middle of the gallery that you cannot see through? Or the walls are curved? And what if, instead of guarding a two-dimensional polygon, you are trying to guard a three-dimensional polyhedron? You could also consider a different set-up, not looking at guards inside a gallery, but guards outside a prison guarding its walls. Mathematicians have found answers to some of these questions (see here), though some proofs have turned out to be quite hard. But they are still working on others. Thirty years on, the problem is still going.

Look for new tools

Gottfried Leibniz (left) and Isaac Newton (right).

There are also questions that are being asked, not by individuals, but by a whole age, crying out for new mathematical tools. Their answers can spawn something of a revolution. A great example is the invention of calculus in the seventeenth century. The question then was, "how can we describe continuous change"? A (modern) example is the speed of a car. It's easy to work out the average speed you travelled at during a car journey: speed is the rate of change of distance per time, so you simply divide the distance you travelled by the time it took to travel it. But of course, you didn't travel at that average speed at every moment of your journey. At some times you will have been going slower and at some times faster, with the speed varying continuously. To work out your exact speed at a particular moment in time, you have to calculate the instantaneous rate of change of distance with respect to time.

The methods for doing this were invented primarily by Gottfried Leibniz and Isaac Newton, although many other people worked on the problem too. And since rates of change crop up all over the place — acceleration is the rate of change of speed with respect to time, growth is the rate of change of size with respect to time, cooling or warming is the rate of change of temperature with respect to time, etc — calculus turned out to be the most powerful tool in all of mathematics, and science, and engineering. (You can find out more about calculus in Making the grade and Making the grade, part II.

Take risks

Not all questions turn out to have interesting answers. Mathematicians simply have to accept the risk that a question they choose to work on may not be solved in their life time (see Fermat's last theorem above), or that it may turn out to have a boring answer. It's all part of the creative process.

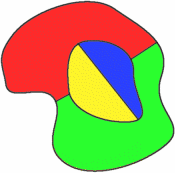
A simple map coloured with four colours.

A famous example of the latter — a boring answer after a lot of work — is the four colour theorem, which says that four colours are enough to colour a map drawn on the plane so that no two neighbouring countries have the same colour (find out more here). The proof of this theorem, when it finally came in the 1970s after mathematicians had been wrestling with the theorem for over a century, was disappointing. It used a brute force approach involving a computer checking through a huge number of possibilities, making sure they did not provide a counter example to the theorem. The approach delivered no new insights at all.

But mathematicians don't like giving up. Just like a cat keeps toying with a mouse, so mathematicians often keep toying with a problem if they don't like the answer that has already been found. They turn it this way and that, looking at it in different light and from different angles. Often it's a new question, a new way of phrasing the problem, that leads to a satisfying answer and new directions in mathematics.

About the author

Marianne Freiberger is Editor of Plus.

About this article

This article was inspired by content on our sister site Wild Maths, which encourages students to explore maths beyond the classroom and designed to nurture mathematical creativity. The site is aimed at 7 to 16 year-olds, but open to all. It provides games, investigations, stories and spaces to explore, where discoveries are to be made. Some have starting points, some a big question and others offer you a free space to investigate.