
Maths behind the rainbow
When the great mathematician Isaac Newton explained the colours of the rainbow with refraction the poet John Keats was horrified. Keats complained (through poetry of course) that a mathematical explanation robbed these marvels of nature of their magic, conquering "all mysteries by rule and line". But as we will see, the mathematical explanation, requiring just the basic geometry of lines and circles, is just as elegant as the rainbows themselves.
Bent on refraction

The visible spectrum from violet (left) to red (right).
The colours of the rainbow are a result of refraction splitting the light into its constituent components, just as happens when light shines through a prism. The white light that arrives from the Sun is a combination of electromagnetic waves with varying frequencies. You see white when this mix of frequencies hits your eye at the same time, but when your eye catches an individual wave on its own, you perceive a particular colour.
Waves with frequencies between around 670 and 780 THz are perceived as shades of violet. On the other end of the spectrum are waves with frequencies between around 400 and 480 THz, which are perceived as shades of red. All the other colours come from frequencies in between these two bands. Electromagnetic waves of other frequencies can't be perceived at all by the human eye.
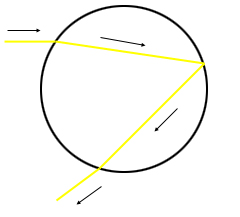
Figure 1: A ray of light being refracted, reflected and then refracted again.
When a ray of sunlight hits a spherical water droplet some of it will be reflected by the surface of the droplet, but some of it will enter it. As it enters, the light ray will be bent, or refracted. It's the same phenomenon you see when you stick a straw in a water glass. The ray then continues until it hits the back of the droplet. Some of the light will exit, but some of it will be reflected back, leaving the droplet on the other side and being refracted again in the process. See figure 1.
Refraction is a result of a ray of light being slowed down as it passes from one medium to another. For a very crude analogy think of pushing a shopping trolley from the road onto grass at an angle: it will change direction because the side of the trolley that hits the grass first will be slowed down first.
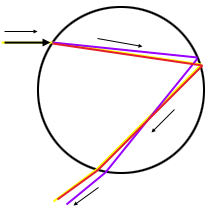
Figure 2: Light of different frequencies is refracted by different amounts.
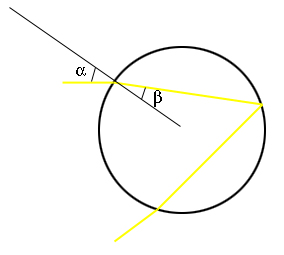
Figure 3: The diagram shows the cross-section of the water droplet containing the incident ray, the refracted ray and the normal. The angles α and β are related by Snell's law.
It's these different refraction angles for the different frequencies of light that gives a rainbow its colours.
Catching rainbow rays
But why do we see each of the colours forming a perfect circular arc? To understand the shape of the rainbow, think of light from the Sun as coming down in parallel rays and striking a particular water droplet in the air. Using Snell's law and the law of reflection (that the angle of incidence equals the angle of reflection), we can work out by how much a ray is deviated in terms of the angle $\alpha$ at which it first hits the droplet. In other words, by what angle it is being turned as it is refracted, reflected and then refracted again (see figure 4). This angle will of course be different for each frequency, or colour of light. By staring hard at figure 4 you can convince yourself that the deviation $D_f(\alpha)$ is given by the formula $$D_f(\alpha)=(\alpha-\beta)+(180^\circ-2\beta)+(\alpha-\beta)=180^\circ+2\alpha-4\beta.$$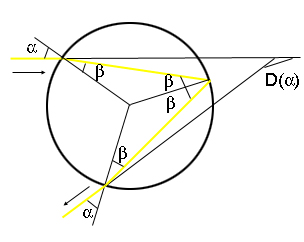
Figure 4: Working out the angle of deviation.
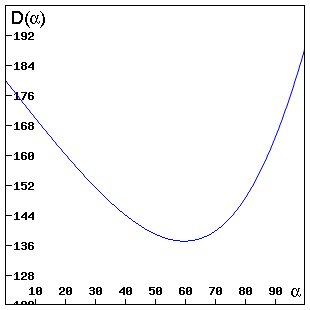
Figure 5: The graph of Df(α).
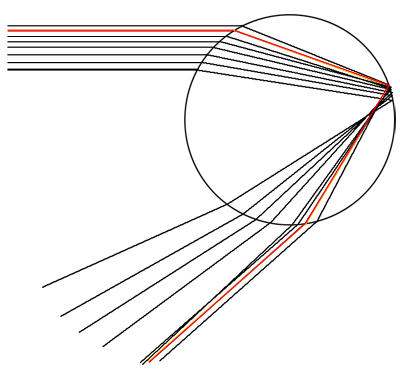
Figure 6: The rainbow ray is shown in red. A cluster of rays emerges from the droplet near the rainbow ray, while rays that emerge elsewhere are more spaced out.
If you don't believe the picture, here is a proof.
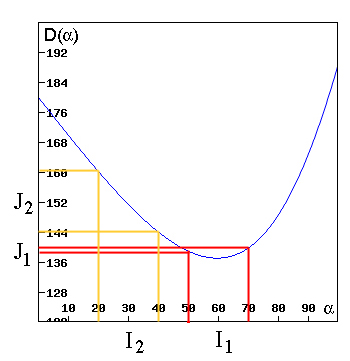
Figure 7: The interval J1 is smaller than the interval J2.
Colour cones
So you see a red dot in the sky for every droplet from which your eye manages to catch an outgoing red rainbow ray. To see where in the sky these droplets are relative to you, let's first work out the exact value of $\alpha_m$. Solving $\frac{d D_f(\alpha)}{d\alpha}=0$ to find the minimum gives $$\alpha_m=\arccos{\sqrt{\frac{n_{f,w}^2-1}{3}}}.$$(See here for the details).
Substituting $n_{f,w}=1.33$ (for our particular shade of red) gives $\alpha_m=59.58^\circ$ and $D_f(\alpha_m)=137.48^\circ$. Now if an emerging rainbow ray from a droplet meets your eye, then this means that the emerging ray makes an angle $r_f=180^\circ-137.48^\circ=42.52^\circ$ with the line $L$ shown in figure 8. It's the line you get from extending the ray of sunlight that would pass straight through your eye if your head wasn't in the way. (Remember we're assuming that the rays from the Sun are parallel.) Let's call $r_f$ the rainbow angle. Of course it depends on the frequency $f$ and therefore on colour.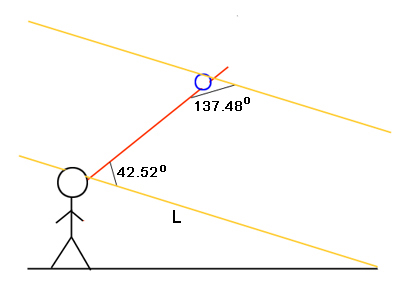
Figure 8: The deviated rainbow ray from your droplet makes a 42.52 degree angle with the line L.
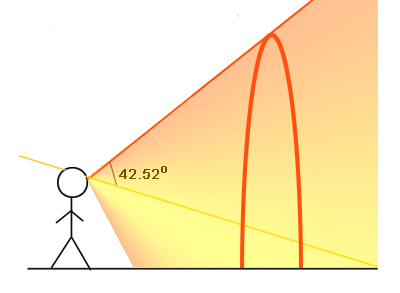
Figure 9: The droplets you see light up in the sky lie on the surface of a cone.
This explanation also shows why you only ever see a rainbow when you're standing with your back to the Sun: that's the only way you can catch rainbow rays coming from droplets. It also explains why the sky appears much brighter below the rainbow than above. Since the vast majority of rays leaving a droplet do so above the rainbow ray (see figure 6), you won't catch any rays from droplets that are "above" the rainbow (that is, outside the cones for the various colours). So you won't see any reflected light from these droplets. However, your eye does catch reflected light from droplets "below" the rainbow (droplets that lie inside the cones) and it's this light that makes the sky below the rainbow appear brighter. It appears as white light because non-rainbow rays for different colours, coming to your eye from different droplets, are mixed together.
The rainbow geometry also shows that any rainbow you see is yours and yours alone: whatever a person standing next to you might see, it'll come from a different set of water droplets and therefore it'll be a different rainbow.

Sometimes, if you are lucky, you might see a second, slightly fainter rainbow above the main one. The secondary rainbow is a result of light rays being reflected twice within the water droplets. The rainbow angles for the various colours are around 51 degrees in this case, which is why the secondary rainbow is seen higher in the sky. The double reflection also means that the colours of the secondary rainbow appear in reverse order, with violet at the bottom and red at the top. Here's the original sketch by René Descartes, who first explained the shape of the rainbow, showing both the primary and secondary rainbow. The double reflection corresponding to the secondary rainbow is traced in red.
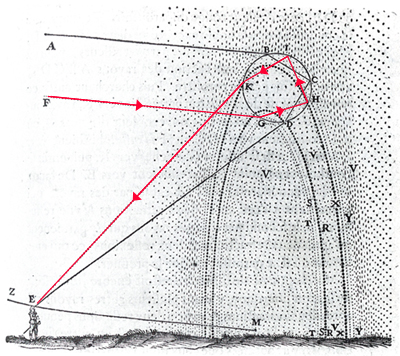
Descartes' sketch of the primary and secondary rainbow.
It is even possible in theory (though it hardly ever happens in practice) to see rainbows coming from three, four or more reflections within the droplets. But I'll leave these calculations to you.
About the author
Marianne Freiberger is co-editor of Plus.
Comments
Anonymous
I have seen triple rainbows and read on the BBC website about the first quadruple rainbow being captured on film (photographic?). At what angles would we see the third and fourth rainbows?
Anonymous
We're trying to find out how much light comes out at a certain angle (represented by D). That depends on D(alpha), as the author states. However, it also depends on the intensity of light as a function of alpha. Much more light falls on the drop between alpha = 0 and alpha = 1 degree than falls on the drop between alpha = 89 degrees and alpha = 90 degrees. (In fact it's more than 100 times as much.)
This does not affect the final result of which angle is the rainbow angle. However, it does affect the distribution of light intensity as a function of D and the article is remiss to ignore it.
Anon
At 89 to 90 degrees the reflection would be almost nil, the light would just go straight through the raindrop and not appear in the rainbow at all.
Anonymous
Great post! In your photo, the secondary rainbow has red at the bottom, which is opposite what is described in the text.
Trusty
Had to re-read this statement about secondary rainbows being reversed, several times, because the author's color description of the "reversal" still matched the first rainbow's order of hues. I'm not math or physics minded, and already being overwhelmed by those complex details, I thought I must be terrible in English comprehension, as well. My reason for even attempting to read this article was to find out why the color blue in a rainbow begins as light blue before transitioning to darker indigo....which becomes a lighter purple, as violet. I wanted to transpose "the color wheel" mixing of primary colors to understand, without taking into account that the bending of light is not the same as if mixing paint. I'm gonna Google Search the angle from the "Light Color Wheel" to see if Sunlight is the same as Computer Screen Light...which it's probably not. I just want to know what causes a Rainbow blue to transition from light to dark, then to light purple. If I had super vision, would the light purple of violet change to a dark purple. However, my mind has not developed neural synapses to comprehend these answers. I wish!
anonymous
photons can only go at speed c, individual encounters within the water apparently lowers the overall light velocity more for blue than for red, as a photon encounters the boundary layer at angle alpha, does it push the lower atom down and the upper atom up as it passes through?
Anonymous
Thanks for the post. I'm confused about one point though. In figure 4, why the light is fully reflected first time but not when exiting? In both cases it makes an angle of beta with the normal. Following the Snell's rule, it should be never fully reflected, if it's source is outside of the water droplet according to my understanding. It should always exit with the angle it enters.
Dwight Propp
It is correct to think that the angle of reflection inside the droplet (beta) is the same as the angle of refraction when the ray first enters. However, it cannot occur that this angle of reflection would reach the critical angle required for total internal reflection, as this would also require that the refracted angle be greater than critical. To achieve that, the incident angle would necessarily have to be greater than 90 degrees, meaning the incident ray would not enter the droplet!
Therefore, all reflection inside the droplet must involve partial reflection and partial transmission.
Choong Yoke Leng
Thank you very much for the explanation though I skipped the part of the maths for calculating the angle between incidence and emerging ray. I have seen double rainbows a few times. I even have a photo of one in this Handphone. I read your article because I was searching for the angle of incidence and emerging ray for a rainbow.