Searching for answers
The search for the missing Malaysia Airlines' flight MH370 was dramatically narrowed last week due to a mathematical analysis of satellite signals from the plane. Contact was lost with the plane's main communication system just after 1am Malaysian time on Saturday 8 March. However, the system automatically responded to regular hourly signals from the satellite network for a further seven hours. After careful analysis of this handful of data points, the search now focuses on an area in the southern Indian Ocean, off the coast of Western Australia.
The analysis was done by Inmarsat, a satellite communications company based in London that was originally established by the International Maritime Organisation in 1979 to enable ships to to call for help in an emergency, no matter how far they were out to sea. The company now provides satellite communications in many different situations including aviation – it's thanks to them that you are able to make calls and use the internet when flying thousands of metres above the ocean.
Even though flight MH370 stopped sending messages in the early hours of Saturday 8 March, Inmarsat scientists realised it would have stayed connected to their network as long as the plane was powered up. If the network's ground stations have not heard from an aircraft for an hour, the ground station sends a short message, called a ping, to the plane. If the plane is still operational it automatically responds, completing what is known as a handshake.
Inmarsat discovered that flight MH370 had made six such hourly handshakes after all other contact with it had been lost. For each handshake the distance of the plane from the known position of the satellite could be calculated from the time the signal took to travel between them. Although less information than for a GPS system (which uses the distances from multiple satellites to pinpoint locations, you can read more in Conic section hide and seek), the scientists could use this data to produced arcs of possible positions for the plane. This indicated two possible routes: one travelling north and one travelling south.
Inmarsat's scientists were able to narrow down the search even further. Still working from just these six handshakes, they built mathematical models of how the frequency of these signals would be effected by the plane's position, speed and direction of travel. This is the famous Doppler effect which also changes the pitch of a siren as an ambulance or police car passes you by (read more in Doppler detectives). By careful modelling of how the doppler effect would change the freqency of the plane's signal in each handshake, for each of the two possible routes, they were able to identify that the southern route was the most likely.
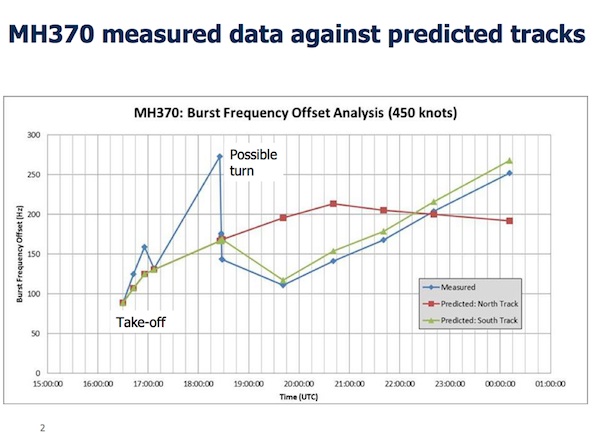
One of the plots showing how the models of the changes in frequency for the southern routes closely matched the observed data for flight MH370.
This is not the first time maths and statistics has been pivotal in searching for a missing plane. In the early hours of June 1, 2009, the Air France flight AF447 disappeared during stormy weather as it flew over the Atlantic ocean. The worst fears of grieving relatives were confirmed just days later, when bodies of some of the 228 passengers and crew and debris from the plane was discovered near the planes' last recorded location. But the answer to why the plane crashed remained unknown for nearly two years, hidden within the black box recorder as it lay undiscovered on the ocean floor.
The black box was eventually found in April 2011, thanks to a new search strategy based on Bayesian statistics. This Bayesian approach allowed Colleen Keller, Lawrence Stone and other statisticians from the scientific consulting company, Metron, to encorporate all the evidence gathered in the previous four search efforts, and assess how the results of these searches altered the likelihood the plane would be found in various search regions.
Such an analysis starts by dividing the whole search area into a grid and assigning a probability to each square that it was the final resting place of the black box. The sum of these probabilities must add to 1 as the black box must be located somewhere in the search area. Then the probability of the black box being in a particular square in the grid is assigned based on various factors such as what is known about the flight of the plane before it disappeared and data from incidents involving similar aircraft. This information forms a prior probability distribution across the whole search area. "This prior probability distribution is a model of what you know before the search starts," says David Spiegelhalter, the Winton Professor for the Public Understanding of Risk at the University of Cambridge. "It's prior to anyone starting to look."
This probability distribution is then revised according to the results of each of the search operations. The prior probabilities are reweighted, essentially multiplied by a number derived from the new evidence. (You can read more about the use of Bayesian statistics in evaluating evidence in It's a match!.) If a grid square was searched and the black box wasn't found, then the probability it is located in that square will decrease. And, as the probabilities across the whole grid must add to 1, the probability the black box is located in the other squares in the grid will increase.
But Spiegelhalter says that the crucial thing in calculating these posterior probabilities is to take into account all the possible ways you could have ended up with the evidence you gathered. For example: "You have to take into account the error rates of your search. What is the probability it was there, but you missed it?" So rather than assuming your search operation was definitive – that you didn't find the black box because it wasn't where you searched – you are very careful to consider all the ways your search operation could have failed when revising your probability distribution.
"This was the crucial element," says Spiegelhalter. "They did a proper weighting, a cold, hard weighting of the evidence, where you have to admit you might have been wrong." This proved to be the key to discovering the black box recorder for Air France flight AF447. Initially the search involved acoustically detecting the beacons in the recorder that would have been triggered as soon as it hit the water. But the recorder was not found during the methodical search of the area close to the last known position of the plane. After searching for the 31 days the beacons could have remained operating, the search moved on to different areas.
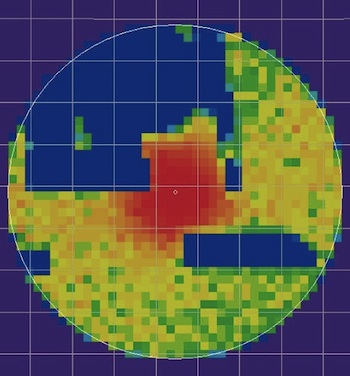
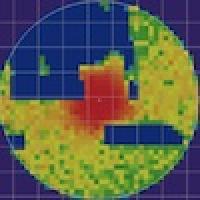
The posterior probability distribution for the location of the flight recorders from flight AF447. The red areas were those calculated to be the most likely locations and were, indeed, where the recorders were located in April 2011.
When Keller and her colleagues analysed the evidence from this search, they were careful to include all the different possibilities, including that the acoustic search missed finding the black box. "In the trade, this is known as extending the conversation," says Spiegelhalter. "It can be quite difficult to understand the probability of missing something, given it's there. So you need to decompose it into intermediate events." In the case of the search for AF447, this meant considering the possibility that both of the two beacons in the recorder may have been destroyed in the crash. Although this seemed very unlikely (they calculated that each beacon had an 80% chance of surviving the crash), the small probability that both beacons had failed drastically changed the posterior probabilities.
"It's a good example of Cromwell's Rule," says Spiegelhalter, referring to the Cromwell's appeal to the Church of Scotland in 1650 to "think it possible you might be mistaken". And this is the real strength of the Bayesian approach. Not only does it allow you to cumulatively integrate your evidence. It also stops you taking too much notice of a single piece of evidence. "Humans find that unbelievably difficult to do. We are too influenced by single events and single narratives." A single big piece of evidence, such as not finding the recorder in an area searched thoroughly while the beacons should still have been operating, clouds our judgement. "Lots of small pieces of evidence can outweigh one big piece, particularly if that big piece may be wrong."
The final posterior probability distribution calculated by Keller and her colleagues said it was most likely the flight recorder would be found in the area close to the last known position of the plane, the same area essentially ruled out by early searches. And indeed, just a week after the search of this area began in 2011, the recorder was found and the reasons for the crash uncovered.
Bayesian searching is now a standard tool in many different areas, including oil exploration as well as search operations. And the new analysis by Inmarsat adds to the tool kit of techniques that can be called upon by future search operations. Mathematical and statistical analyses are of course, far from the minds of the relatives of the passengers and crew of these missing planes. But such analyses could yield the vital clue for solving the riddles of what happens to their loved ones. It is encouraging that such technical analysis is already contributing to the hunt for the missing flight MH370, and we hope that the relatives have the answers they need very soon.