On a rainy night last month, in an ancient hall down a hidden alleyway in the centre of London, Bernard Silverman, Chief Scientific Advisor to the Home Office, revealed a surprising secret... ancient mathematics is at the heart of a very modern game of hide and seek.

During his talk, the annual joint London Mathematical Society/Gresham College lecture, Silverman explained how mathematics can be used to tackle crime, manage migration and counter terrorism. For example, the Migration Advisory Committee has used statistics to show that neither the popular perception of "migrants taking our jobs" nor the classical economic theory of migration is true (you can read the report on the MAC website). The effect of explosions on buildings can be predicted using finite element analysis. And most intriguingly, the mathematics of ancient Greece is used to keep track of offenders and undertake search and rescue operations.

Euclid and Archimedes are just two of the Greek mathematicians that studied conic sections – the shapes created by slicing through a double cone with a flat plane. If the plane is perpendicular to the axis of the double cone the intersection is a circle and if it's at an angle less than the slope of the cone's side it's an ellipse. If the plane is angled parallel to the side of the cone the intersection is a parabola and if it is angled so as to cut through both cones the intersection is a hyperbola. (You can read more about conic sections in the article on our sister site nrich.)

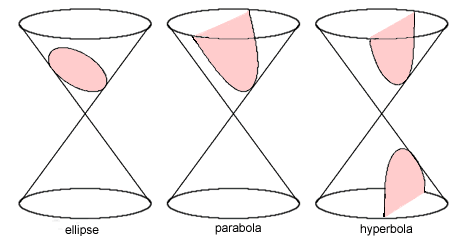
The conic sections (the circle can be thought of a special type of ellipse)
(Image from nrich)

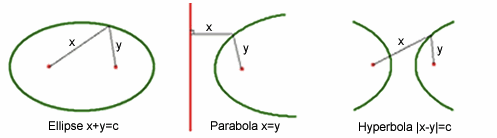
As well as having a physical description in terms of slicing through a cone, these shapes also have a very clear mathematical description: a circle is the locus of points the same distance from the centre (the focus of the circle); an ellipse is the locus of points with the same sum of distances from two foci (x+y equals a constant c in the image above); a hyperbola is the locus of points with the same difference of distances from two foci (|x-y| equals a constant c); and a parabola is the locus of points equidistant from a focus and a straight line called the directrix (x=y).

Skip forward a couple of millennia and the mathematical properties of the conic sections have a very modern application. Now we are all used to being able to find our location (even if navigationally challenged like myself) thanks the the GPS feature in many mobile phones. GPS satellites (of which there are about 9 overhead at any one time) constantly send out signals giving their precise location and the time the signal was sent. The GPS receiver in my phone receives this signal and can calculate my distance, d, from the satellite (equal to the time it takes the signal to reach me multiplied by the speed of light), placing me somewhere on a circle with radius d centred on the location of that satellite. Similarly, the signal from two other GPS satellites places me on two more circles and the intersection of these three circles pinpoints my location. (Working in two dimensions is a slight simplification but is feasible by assuming we are on the surface of the earth, see How to find your way around the Arctic for more details.)

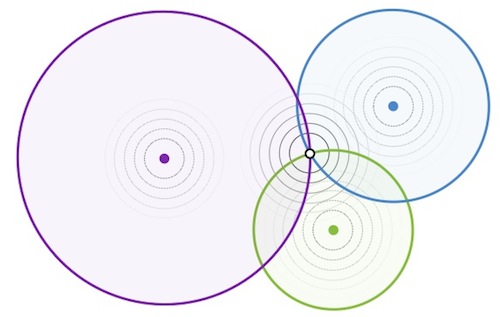
The intersection of three circles centred on the GPS satellites pinpoints the target's location (Image courtesy of Bernard Silverman)

This method, called trilateration, requires three transmitters (the GPS satellites in this case) to each send a transmission in order to determine someone's location. However another conic section can make this process more efficient.

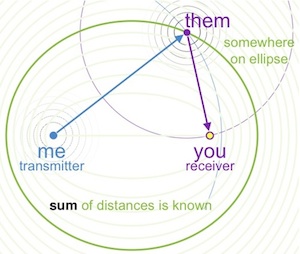
Multireceiver radar places the target on an ellipse (given by x+y=c, where c is a constant) where the transmitter (me) and the receiver (you) are at the foci (Image courtesy of Bernard Silverman)

Multireceiver radar uses intersecting ellipses to find a target's location. This time I transmit a signal to which the target replies. Then, at another location, you have a receiver which picks up the reply. The initial signal I sent has travelled an unknown distance, x, between myself and the target, and the reply has travelled another unknown distance, y, between the target and you. Although we don't know these distances x and y, we do know their sum x+y is the total time from when I sent the signal to when you received the reply, multiplied by the speed of light. Therefore the target is somewhere on an ellipse with you and myself as the foci. By using three receivers we can intersect the three resulting ellipses to find the target's location, this time using just my lone transmitter and only two transmissions (my initial signal and the target's reply).

One downside of this method is that it assumes the target will immediately reply to any signal we send; and what if we can't guarantee they'd respond? Another conic section provides the answer: hyperbolic trilateration.

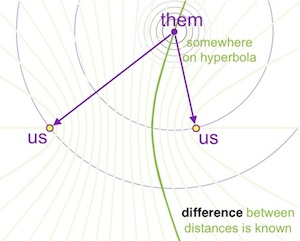
Multilateration places the target on the hyperbola (given by |x-y|=c, where c is a constant) with the two receivers at the foci (Image courtesy of Bernard Silverman)

Hyperbolae allow us to locate a target by silently listening for any signals they transmit. When a transmission is received in two different locations we know it has travelled an unknown distance, x, from the target to the first receiver and an unknown distance, y, from the target to the second receiver. Then the difference between these two distances is just the difference in flight times of these two paths (ie, the measured difference between the times at which the signal was received at the two locations) multiplied by the speed of light. Therefore the target lies somewhere on the hyperbola with foci at the two receivers. The intersection of three such hyperbolae (one for each pair amongst three receivers) locates the target using only the signals they have transmitted.

This covert technique, called multilateration, was used in WWI to locate enemy artillery ranges by listening to the sound of their gunfire. Today this 2000 year old mathematics is used to find lost souls and uncover hidden enemies.

You can watch all of Silverman's lecture online at the Gresham website