
It's a match!
Whether it's reading the newspaper or watching CSI, the evidence that often closes the case is a DNA match. Our DNA is almost always unique, so at first glance it might seem that if the police have matched a suspect's DNA to evidence from the crime scene, then the case is closed. But it isn't as simple as that. Some statistical thinking is required to understand exactly what a match is, and importantly, how juries should assess this as part of the evidence in a trial.
What is a DNA match?

Humans have 23 pairs of chromosomes Image by Jane Ades, NHGRI.
The first thing to understand is that a DNA match isn't a complete match of the whole DNA genome. Your genome — all of the different long strings of DNA in each of your cells — is unique to almost everyone (the only exception being identical twins, triplets...) Each long string of DNA is wrapped into a bundle called a chromosome. We each have 23 pairs of chromosomes: the two chromosomes in each pair correspond to the same sequence of genes, but one comes from your mother and one from your father. These sequences are similar, in that they correspond to the same sequence of genes, but not identical: your mother and father may have had different versions (called alleles) of a gene, for example if your mother had blond hair and your father black hair. (You can read a good introduction to DNA and chromosomes on the Hopes site at Stanford.)
At certain places on the chromosomes, repeated patterns can be found in the genetic code (these are called short tandem repeats or STR). For example, at position D7S280, found on chromosome 7, the word GATA is repeated between 6 and 15 times in our DNA, the exact number of repeats varying from person to person.
The following example has 12 repeats of the pattern GATA (shown in alternating red and green text).
| AATTTTTGTATTTTTTTTAGAGACGGGGTTTCACCATGTTGGTCAGGCTGACTATGGAGTTATTTTAAGGTTAATATATATAAAGGGTATGATAGAACAC |
| TTGTCATAGTTTAGAACGAACTAACGATAGATAGATAGATAGATAGATAGATAGATAGATAGATAGATAGATAGACAGATTGATAGTTTTTTTTTATCTC |
| ACTAAATAGTCTATAGTAAACATTTAATTACCAATATTTGGTGCAATTCTGTCAATGAGGATAAATGTGGAATCGTTATAATTCTTAAGAATATATATTC |
| CCTCTGAGTTTTTGATACCTCAGATTTTAAGGCC |
A DNA profile is simply a count of these short tandem repeats at particular locations on the genome. The CODIS database developed by the FBI uses STR at 13 places, and the UK National DNA database uses STR at 10 places.
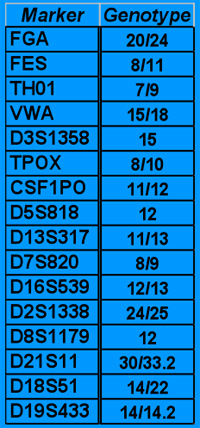
A typical DNA profile.
For a particular DNA sample, the number of repeats at each STR marker (called the genotype for that marker) is counted.
For example in the profile on the left, the first STR marker FGA, has one strand of DNA with 20 repeats of the code word and the other with 24 (one strand from their mother's DNA and one from their father's), and so has genotype 20/24. But further down, the STR marker D3S1358 has 15 repeats on both strands, and so has the genotype of 15. Occasionally there are glitches in the repeats of the code word, which are represented by genotypes with decimal points, such as the 33.2 for one of the alleles of the gene at D21S11.
Rare but not necessarily unique
In a criminal case we'll typically have two profiles, one from the scene of the crime and one from the suspect. And if it's come to court they probably look identical.
Because we're only looking at something like 13 different places on the genome, it's not logically impossible for two entirely unrelated people to match just by chance. We need to know roughly how unlikely that is. This can be calculated from the proportion of the population that has each of the different numbers of repeats at the 13 locations. These allele frequencies are estimated from databases that are collected from forensic laboratories.
| Allele of TH01 | Frequency |
|---|---|
| 4 | 0.001 |
| 5 | 0.001 |
| 6 | 0.266 |
| 7 | 0.160 |
| 8 | 0.135 |
| 9 | 0.199 |
| 9.3 | 0.200 |
| 10 | 0.038 |
| 11 | 0.001 |
This table lists the frequencies for the different alleles of the gene at marker TH01. Some alleles are very rare — only 1 in 1000 people have 4 repeats of the code word — while some are more common — more than 1 in 4 people have 6 repeats at this location. Similar frequency data exists for all the STR markers used in DNA profiles. These frequency estimates do vary according to race, so frequency databases are compiled for different racial groups.
In order to use these allele frequencies to calculate how rare a profile is we have to make some genetic assumptions. The STR markers used in DNA profiles are on different chromosomes, and we assume that they are independent: the genotype of the marker on one chromosome has no effect on the genotype of another marker on another chromosome. We also assume that we are working with a randomly mating population: in essence that we randomly draw our parents from the population with respect to the genotypes of the STR markers in their profiles. Then the two strands in each pair of chromosomes, one strand from each of our parents, can be thought of as independent. This relies on the assumption that the STR markers chosen for DNA profiles have no genetic function — they appear to be junk DNA that doesn't result in any visible or observable traits that affect health or survival. If these genes coded for beauty or affected our health then it could make a big difference to how they are passed on from our parents.
The independence of the markers used in the profile means that to calculate how rare a profile is, we can simply multiply the frequencies for the independent markers together to get the match probability — the probability that a random person in the population will have that DNA profile.
Although the individual allele frequencies may be in the order of, say, 20% that is 1/5, as you are multiplying a lot of these together you end up with a very small number. It's similar to the lottery: getting one ball right is quite likely, but the chance of getting them all right is 1 in 14 million. The match probabilities calculated for DNA profiles today are usually in the order of 1 in a billion.
How not to use DNA profile evidence

Imagine you are in the jury for a criminal trial. We'll use a real case as an example: the trial of Denis John Adams for sexual assault in 1995. The only incriminating evidence presented by the prosecution was that Adams' DNA profile matched a crime sample taken from the victim that was accepted as coming from the culprit. The estimates of the match probability in this case ranged from 1 in 2 million, to 1 in 200 million. For the moment we'll use the value of 1 in 2 million.
The obvious but absolutely wrong thing to do is to say: "The rarity of this profile is 1 in 2 million. So there's only a 1 in 2 million chance that it came from someone other than the suspect... We've got him!"
This error is a form of the Prosecutor's Fallacy — misinterpreting the match probability (the probability that a random person's profile matches the crime sample) as the probability this particular person is innocent on the basis of the evidence. And as the match probability is very small, just 1 in 2 million, then we mistakenly think that:
Probability that Adams is guilty $= 1 - \frac{1}{2000000}$
and that's as close to 1 as anything you can imagine, so you can bang him away. (You can read more about the Prosecutor's Fallacy on Plus.)
So what should you do with the match probability?
We have a particular profile that happens to be identical to both Adams and the sample taken from the victim. Whether the crime sample came from Adams or not we don't know, but it has the same DNA profile. But that profile also exists in the population at large. And the question is, who else could there be out there with that profile?
You can't treat the match probability as meaningful in itself. The match probability tells how likely it is that a random person's DNA profile will match the crime sample. To take the match probability into account we need to calculate the likelihood ratio:
$$LR = \frac{\mbox{(Probability of observing the evidence if the defendant is GUILTY)}}{\mbox{(Probability of observing the evidence if the defendant is INNOCENT)}}.$$
The likelihood ratio measures the impact of the evidence. For the Adams case, if he was guilty then his DNA profile would definitely match the crime sample, and so the probability of observing this evidence is 1. (For other evidence, the probability of observing the evidence if the defendant is guilty might not be 1, as we shall see later.) And if Adams wasn't the culprit then the probability of observing the evidence (the denominator in the LR) is just the match probability of around 1 in 2 million.
This gives:
LR = 1 / (Match probability) ~ 2 million
So, the likelihood ratio tells us that we are 2 million times more likely to observe the evidence if Adams is guilty than if he is innocent.
However, by considering the match probability in isolation we are only looking at the probability of the DNA profile evidence. And as it might be possible that this evidence could occur even if Adams is innocent, it is only indirectly related to the probability of his guilt.
Presumption of innocence
Before introducing any evidence, the accused should be considered as no more likely to be guilty that any other 'random' member of the appropriate population. You can think of this as a mathematical translation of the legal presumption of innocence.

The presumption of innocence principle can be translated into mathematics.
From the facts of the crime it is reasonable to suppose that the culprit was a man aged between 18 and 60 who is likely to live locally. There were about 150,000 of these, and we could expand this to, say, 200,000 to allow some possibility of a non-local culprit. Before any explicit evidence is presented all that is known about Adams at this point is that he matches these characteristics. Therefore, assuming that Adams is no more likely to be guilty than any man in the local area we can estimate that there is a 1 in 200,000 chance that he is guilty.
This initial figure of 1 in 200,000 is called the prior odds of his guilt. Starting from this position of presumed innocence, we can now use the likelihood ratio, LR, to take into account the DNA profile evidence. (The following is a restatement of Bayes Theorem of conditional probability — you can read more about Bayes Theorem and conditional probability in Plus.)
Posterior odds of guilt = LR x prior odds = 2 million x (1/200,000) = 10
This is the posterior odds of guilt:, it's the ratio of chances favouring guilt to chances favouring innocence. The posterior odds is 10 chances to 1, so 10 chances out of a total of 11, giving a probability of about 91% that he is guilty. In the court of public opinion he is probably guilty, it's beyond 90%. But is that good enough for a court of law, is that beyond reasonable doubt?
Taking into account other evidence
In this particular case there was other evidence to consider, and all the other evidence supported Adams' claim of innocence. The arrest was made quite a long time after the crime: Adams was pulled in for some other offence, and a routine run through the DNA criminal database found that he matched the crime sample from this old case. In a subsequent identity parade the original victim of the crime did not pick Adams out of the line up and even said that it was not the man who attacked her — as far as she was concerned they'd got the wrong man.
Adams also had an alibi as his girlfriend said they had spent the night together. None of this evidence was completely definitive, but it certainly supported his innocence rather than his guilt. And there was no other evidence, apart from the DNA profile, linking Adams to the crime.
By trying to numerically measure, in ball park figures, the strength of this other evidence, we can combine it with the evidence we've already got. If Adams was guilty there is still a small chance, which we might estimate as 10%, that the victim may still not be able to identify him (the victim may not have seen Adams properly or have trouble remembering his face). However we feel quite confident, we estimate 90% certain, that if Adams is innocent that the victim wouldn't identify him. This leads to the likelihood ratio of the impact of the victim not identifying Adams as:
LRvictim = 0.1/0.9 = 1/9.
Considering the evidence of Adams' girlfriend giving him an alibi, there is a fair chance, which we might estimate to be 25%, that his girlfriend would lie and say they spent the night together. If he is innocent, we might estimate that there was a 50% chance that they happened to spend the night together, giving him an alibi.This results in the likelihood ratio of the impact of the alibi as evidence as:
LRalibi = 0.25 / 0.5 = 1/2.
After taking into account the DNA profile evidence we estimated the odds of Adams' guilt to be 10 to 1. This then becomes the prior odds of guilt before we take into account the new evidence from the victim and Adams' girlfriend. Using the same argument as before, we calculate that, after bringing in the additional evidence, the posterior odds of Adams' guilt is:
Posterior odds = LRvictim x LRalibi x prior odds = 1/9 x 1/2 x 10 = 5/9
So the odds that Adams is guilty after all the evidence is considered is now 5 chances to 9 chances, that is 5/14 or 35% chance that he is guilty. Even in the court of public opinion, you would think that this would be an argument for Adams' innocence.
If we had made the mistake of using the Prosecutor's Fallacy, interpreting the match probability as the probability of innocence, there would be no way of incorporating any other evidence — there's just no room for bringing it in. Whereas the correct calculations, using the likelihood ratio to calculate posterior odds of guilt, do account for the fact that this is just one item in the totality of the evidence.
This argument of updating our prior odds of guilt using the likelihood ratios for the DNA profile and other evidence was presented at the trial, with the juror's encouraged to make their own estimates for the probabilities involved for the other evidence. But this argument may well have been lost on the jury, who — perhaps subconsciously swayed by a Prosecutor's Fallacy interpretation of the match probability — convicted. In a subsequent appeal by Adams the statistical argument was actually dismissed on the grounds that it "usurps the function of jury" which "must apply common sense". Noble sentiments perhaps; but problematic when common sense can be such a poor guide to handling statistical evidence.
The number of zeroes matters
In the Adams case the match probability quoted ranged from 1 in 2 million to 1 in 200 million. One infinitesimally small number may not seem that different from another, but it turns out that the number of zeroes does matter. Using the same arguments as above, the range of match probabilities had the following effect:
| Match probability | 1/200m | 1/20m | 1/2m |
| Posterior prob of guilt | 98% | 85% | 35% |
The match probabilities that are routinely quoted now are in the order of 1 in a billion. At this level of accuracy they are much harder to overturn, but not impossible. The most convincing arguments would either be based on laboratory error, contamination, or deliberate fraud.
But even though the accuracy of DNA profiling has increased to produce these astronomical match probabilities, such as 1 in a billion, it is still important to recognise the process that you need to go through to assess this evidence.
Unfortunately there are still few jurors, lawyers and judges who understand the statistical subtleties of such evidence. However there are signs that things are improving in a very small way. There are a number of judges and lawyers who understand the issues and care about them and want to spread good practice. And a working party set up by the Royal Statistical Society is bringing statisticians and lawyers together to understand the issues.
What's problematic is not so much that people don't appreciate the problems, that is the case in many fields. The real difficulty is that people don't appreciate that they don't appreciate the problems — they don't even realise that there is a problem. It all looks so straightforward, instead of incredibly subtle. The correct computations needed to understand statistical evidence such as DNA profile matches are not mathematically difficult, it's simply arithmetic. But knowing what the correct computations are is something that is not many people understand.
About the author

Rachel Thomas is co-editor of Plus. She interviewed Philip Dawid, Professor of Statistics at the University of Cambridge. Professor Dawid has been an expert witness in a number of legal cases involving DNA profiling.
This article now forms part of our coverage of the cutting-edge research done at the Isaac Newton Institute for Mathematical Sciences (INI) in Cambridge. The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.

Comments
Anonymous
I found that this article explained quite a bit of information that I had never quite understood. One aspect of DNA matching probabilities that would mitigate most of the uncertainty would be to increase the number of STR markers. By adding two or three more markers would increase the certainty of identification by a factor of 50 to 1000, making the probability of mis-identification nil.
Anonymous
Hi,
Prof. Dawid and Ms Thomas have done an outstanding job in explaining how the DNA Profiles are matched...err...compared.
Thank you!
Best,
HW
Anonymous
EXCELLENT ARTICLE. Completed MBA in 1980. Favorite class was statistics with a FANTASTIC instructor. Your explanations took me back to his classes as he advocated making statistics relevant to practical issues. Thank you!
Anonymous
EXCELLENT ARTICLE. Completed MBA in 1980. Favorite class was statistics with a FANTASTIC instructor. Your explanations took me back to his classes as he advocated making statistics relevant to practical issues. Thank you!
Anonymous
I followed your article arduently and it is very informative. However, the case I am working on says the dna probability is only 1:4000. Trying to understand how to apply the equations to such a small number is proving difficult for me. Can someone help me out?
Anonymous
The odds are 1/3999.
Phillys curtis
I'm trying to figure out probability of guilt with a 1 of 1300... I read your article but I'm more confused now. Is filing an appeal even worth it with these numbers?
Peter
Great article, no doubt.
Comes with a flaw towards the end, though.
It says 'Unfortunately there are still few jurors, lawyers, and judges who understand the statistical subtleties of such evidence'.
I bet you wanted to say 'Unfortunately there are still few jurors, lawyers, and judges who DO NOT understand the statistical subtleties of such evidence'
Bush
How do you understand a number for a DNA test to prove innocent or not, when document is saying that the DNA profile was calculated for the African American,Caucasian,and Hispanic population groups and was found to be more common than approximately 1in 52 octillion unrelated individuals.