Doppler detectives

08/12/2003

You may not realise it, but you intuitively use the Doppler effect whenever you are alerted to an ambulance or police car coming your way by the rising pitch of its siren. Now Nigel Seddon and Trevor Bearpark, from BAE systems in Bristol, have observed the Inverse Doppler effect for the first time.

The Doppler effect is the shifting of a wave's frequency caused by the relative motion of an observer and the wave source. This motion causes the frequency of the wave to increase as the source and observer move towards each other and decrease as they move apart. For example, an ambulance racing up the road with sirens blaring is catching up with the wavefronts ahead of it, and moving away from those behind it (sound travels in all directions from the siren). This causes the sound wave ahead of the ambulance to bunch up, and the one behind to spread out, resulting in higher and lower frequencies respectively. A person standing up the road will hear the ambulance's siren at a higher frequency - a higher pitch - as it approaches, then briefly, as the ambulance passes by, at the same pitch as the ambulance driver does, and finally at a lower pitch as the ambulance heads away (see below for a more detailed explanation).

As well as alerting us to oncoming ambulances and police cars, the Doppler effect has also proved useful in radar, medical technology and astronomy. Now Seddon and Bearpark are hoping to put the Inverse Doppler effect to equally good use.

The Inverse Doppler effect - first predicted 60 years ago, and never observed until now - occurs when the waves from an oncoming source have a decreased, rather than increased, frequency; and the waves from a receding source have an increased frequency. To observe the effect, Seddon and Bearpark had to look at waves in an anomalously dispersive medium, in their case an electrical transmission line with some unusual properties.

In a medium with normal dispersion, the phase of the wave (the position of, say, the crest of the wave) moves in the same direction as the energy of the wave. However, in a medium with anomalous dispersion, the energy and the phase of the wave move in opposite directions (see past news stories: Light bends the 'wrong' way from Issue 15 and Faster than light from Issue 12, for discoveries involving other types of anomalous dispersion).

The researchers set up their experiment, reported in a recent issue of Science, so that when a pulse of current was fed into the transmission line it caused the magnetic properties of the material to change. The pulse became a moving boundary between the magnetic and non-magnetic regions and also generated a faster-moving radio frequency (RF) wave. The experiment was designed so that the RF wave eventually caught up with and reflected off the moving boundary, creating the "siren" (the reflected RF wave) and the "ambulance" (the moving boundary) of the example above. But due to the anomalous nature of the material, the receding boundary reflected the RF wave with a higher frequency, contrary to the conventional Doppler effect. Seddon told Science they were flabbergasted by the result, and that "for a good hour we just played with the experiment".

Because the technique can create a wide range of Inverse Doppler shifts with multiple frequencies, Seddon and Bearpark hope it will lead to highly tunable radiation sources that could be used in areas such as medicine and communications technology. Perhaps one day the Inverse Doppler effect may, just like its more familiar relative, come in handy for dodging emergencies.

Here it comes...

An ambulance, with its siren on, is emitting a sound wave that satisfies the wave equation $v=\lambda f$ , where $v$ is the speed of sound (about $340$ metres per second), $\lambda$ is the wavelength and $f$ is the frequency. The wave radiates out from the ambulance in all directions, the wavefronts shown as circles in the diagram.

If the ambulance is stationary and you are standing up the road from it, you will hear the siren at the same pitch as the driver - the wavefronts will be $\lambda$ metres apart and will reach you every $1/f$ seconds.

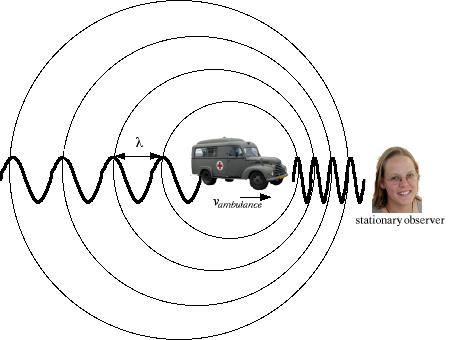
The wave-fronts bunch up in front of the ambulance and spread out behind it

If the ambulance is moving towards you with a speed of $v_{ambulance}$ metres per second, the siren's soundwave still appears to you be travelling at the same speed $v$ (you are at rest relative to the medium - air - that the sound wave is travelling in), but its wavelength and hence frequency will seem different to those of the soundwave heard by the driver.

The siren still emits wavefronts every $1/f=\lambda /v$ seconds, but during this time the ambulance will move toward you by $v_{ambulance} \times \lambda /v$ metres, causing the wavefronts to bunch up in front of the ambulance. The wavelength (the distance between wavefronts) appears to you, and anyone else standing ahead of the ambulance, as $\lambda _{you} = \lambda - \lambda /v$ metres, meaning that you hear the soundwave at an increased frequency of $f_{you}=v/\lambda _{you}=f \times v / (v-v_{ambulance})$ . Similarly, the wavefronts for someone behind the ambulance spread out as it moves away.

When a source, this time something like a fighter jet, travels at a speed greater than the speed of sound, it actually outruns the sound waves, and is said to break the sound barrier, and arrives before the sound does. (Image from the http://www.news.navy.mil/ US Navy)

In another scenario, imagine moving at a speed of $v_{you}$ metres per second towards the stationary ambulance with its siren blaring. Then the sound waves wouldn't bunch up as the source would not be moving. Instead the speed of the sound would appear higher to you as you are moving relative to the medium the wave is travelling in.

In this case, the speed of the wave for you is now $v+v_{you}$ and, from the wave equation, you hear the wave's frequency as $f_{you}=(v+v_{you}) / \lambda =f \times (v+v_{you}) / v$ . Similarly, the speed of the wave seems to be less if you are moving away from a stationary source.

Together, these results give the Doppler equation:

$f_{observer}=f\times \frac{(v\pm v_{observer})}{(v\mp v_{source})},$

where the $+$ and $-$ signs before $v_{observer}$ indicate whether the observer is moving towards or away from the source, respectively; and those before $v_{source}$ whether the source is moving away from or towards the observer, respectively.

You can read more about the Doppler effect and sonic booms from Kettering University.