
Spheres within spheres: A journey through many dimensions
There's been an exciting breakthrough in the field of topology: a group of mathematicians have disproved the telescope conjecture. It had been famous in the field as the last of a whole series of conjectures, formulated by Douglas Ravenel in 1984, to remain unsolved.
The team announced their result at an Oxford conference called A Panorama of Homotopy Theory, part of a programme organised by the Isaac Newton Institute for Mathematical Sciences in Cambridge (INI). And since we collaborate with the INI we were lucky enough to talk to Tomer Schlank and Jeremy Hahn, who proved the result alongside Robert Burklund and Ishan Levy. We asked them to explain their work in the simplest terms possible. Here is what they told us.
What is topology?
Topology takes the same relaxed approach to geometric shapes that we tend to take in everyday life. When we say that a golf ball is spherical we don't care about its many dimples, which mean that, strictly speaking, it's anything but a perfect sphere. Similarly we think of oranges and apples as round, even though they can be decidedly knobbly.
Topology captures this tolerance to deformation. Two shapes are considered topologically the same if one can be transformed into the other by squeezing or stretching, but without cutting or glueing. In this sense, golf balls, oranges and apples, as well as deflated footballs, are all the same. Similarly, a donut is topologically the same as a coffee cup, as the animated gif below shows. It's not the same as a sphere, however, because the only way to turn a sphere into a donut would be to cut holes into it and glue together the edges.
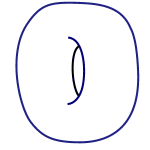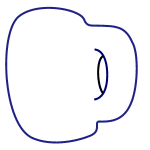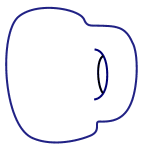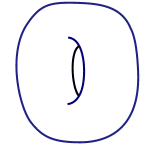
A mug turning into a donut turning into a mug.
What differentiates the donut (technically the torus) from a sphere is that the torus has a hole while the sphere does not. In fact, holes are hugely important in topology. Mathematicians have proved that many surfaces that naturally spring to mind are topologically equivalent to either a sphere (with zero holes), the torus (which has one hole), or a torus with two holes, three holes, etc. The number of holes is what defines such a surface in the topological sense (for a little more detail, see here.)

A sphere, a torus, a surface with two holes, and a surface with three holes.
Going loopy
The question you might now ask is "what is a hole"? It's quite clear to us when we look at a torus that it does have a hole, but once you try to put the property of "having a hole" into words, things get a little slippery.
Here circles come to the rescue. Any circle you might draw on a topological sphere can be contracted to a point. For a topological torus, or any other surface with holes, that's not necessarily true: if the circle winds around a hole, you can push it and nudge it as much as you like, it'll never contract to a single point without pinching the surface.
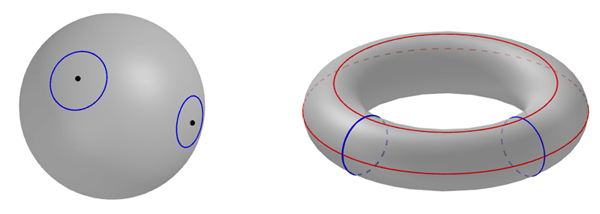
Circles on the surface of the sphere shown on the left can be contracted to a point, for example to their centre points. The blue and red circles drawn on the torus shown on the right cannot be contracted to points because they wind around the hole. Circles of the same colour can be transformed into each other without cutting and glueing. They are homotopic to each other. On the sphere all circles are homotopic to the simplest circle of them all: one that has a radius of 0 so it's just a point. On the torus, however, there are different types of circles defined by how they wind around the hole.
Now if your topological sphere is a golf ball, or your topological torus a wonky donut, then it's impossible to draw a perfect circle on either because of all the dimples and bulges. But we don't worry about this. All we're after is general circleiness, that is, we're considering closed loops.
We also don't distinguish between loops that can be turned into one another without cutting, for example by sliding them along the surface, stretching, or squeezing. Such loops can be considered equivalent. This then divides the collection of loops you can draw on the surface into equivalence classes. Two loops belong to the same class if one can be deformed into the other without cutting. In the figure above, loops of the same colour belong to the same equivalence class.
All this can be made mathematically precise: the equivalence classes of loops on a surface are called homotopy classes. The collection of all these equivalence classes is called a homotopy group of the surface. The exact make-up of this homotopy group gives information about the holes of the surface, and therefore tells you a lot about the surface itself (and yes, it forms a mathematical group). You can find out more here.
Two-dimensional holes
Once you've realised that holes are important in characterising surfaces, and that loops are important in characterising holes, you might ask yourself how you can push this idea further.
So far we have thought about the loops we can draw on a surface, in other words, about all the possible ways we can continuously map a circle on the surface. To map the circle simply means to assign to each point on the circle a point on the surface, and to do so continuously means that there are no gaps in the resulting loop you get on the surface.
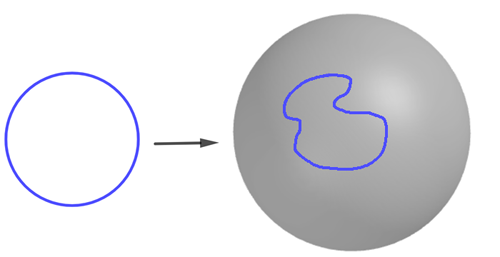
The blue loop shown on the sphere is a deformed version of a circle.Technically, it's the image of a continuous map from the circle to the sphere.
A circle is the one-dimensional analogue of a sphere. So what if we go up a dimension and look at all the ways we can continuously map a sphere to our surface? If your surface is itself a topological sphere, say a deflated football, then it's easy to imagine how you could do this. You deform the sphere until it has the exact same shape as the football and then assign to each point on the deformed sphere the corresponding point on the football.

It's easy to think of a way of continuously mapping a sphere to the deflated football.
It's also easy to see that you can map a sphere to a shape that contains a component that is a topological sphere, as in the figure below.
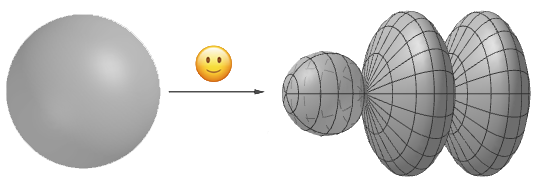
It's possible to continuously map the sphere to the spherical blob on the left side of the shape on the right.
If the surface you are maping to is a topological torus, however, there's no meaningful way of mapping a sphere to it. The hole is proving awkward again.
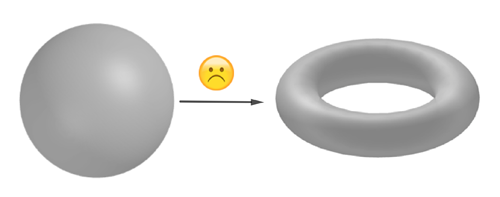
It's difficult to think of a way of mapping a sphere to a torus without either cutting it open or squashing it to form a two-dimensional patch you can then imagine sticking onto the torus. Such a patch is homotopically equivalent to a point. So up to homotopy, the only continuous map from the sphere to the torus is the trivial one, which takes the entire sphere to a single point.
In the first two examples, once the sphere is mapped to the surface, it's impossible to shrink it down to a point without deforming the surface itself. That's because it encloses what you might think of as a two-dimensional hole: the inside of the topological sphere you're mapping to.
"A sphere doesn't have any one-dimensional holes because every time you draw a loop you can contract it," says Tomer Schlank. "But a sphere does have a two-dimensional hole because you can [map another sphere onto it] that can't be contracted. It's not immediately obvious, but it's not hard to prove, that for a torus you don't have two-dimensional holes."
Again all this intuition can be made mathematically precise. And in analogy to what we saw above regarding loops, you end up with a homotopy group of your surface which tells you about the existence of two-dimensional holes. Loosely speaking, the group comes from looking at all the ways you can continuously map a sphere to your surface and seeing if those mapped spheres can be contracted to points.
Higher dimensional holes and shapes
You might now be able to guess where this is going. The circle is a one-dimensional object and the sphere is a surface, so it's two-dimensional. Although we can't visualise higher-dimensional spheres, mathematicians have a way of defining them, so you can work with them just as you can work with circles or ordinary spheres (find out more here).
In analogy to the above you can now define homotopy groups that arise from mapping higher-dimensional spheres into a given shape of interest. These groups will give you information about what you can think of as higher-dimensional holes in your shape.
"Something that is kind of surprising, and was not expected when the notion of homotopy groups was defined, is that you [can] have high-dimensional holes inside low-dimensional spheres," explains Schlank. "For example, you can write down a continuous map from a 3-dimensional sphere to a 2-dimensional sphere that cannot be contracted into a point." This means that the two-dimensional sphere has a three-dimensional hole. It goes beyond what we can visualise, but the figure below is an illustration of this mapping. You don't need to understand it — we include it here as evidence that mathematicians do have a clear idea of what they are talking about.

This image illustrates the Hopf fibration, a non-trivial mapping from the three-dimensional sphere to the two-dimensional sphere. You can find out more about how to interpret this figure here. Figure: Niles Johnson, CC BY 4.0.
We can now ask if the two-dimensional sphere has any four, five, six, etc dimensional holes. More generally, given a sphere of some dimension $n$, you can ask if it has holes of dimension $m$. The corresponding homotopy groups are usually denoted by $\pi_m(S^n)$. The $m$ in the subscript is the dimension of the holes you're after and the $n$ in the superscript tells you you're looking for these holes in the $n$-dimensional sphere.
"Understanding the general question of what are the [homotopy groups coming from maps between spheres] is still one of the most important questions in the field of homotopy theory," says Schlank. In other words, mathematicians would ideally like to understand the homotopy groups $\pi_m(S^n)$ for all possible combinations of $m$ and $n.$
The telescope conjecture proposed a method for understanding some of these homotopy groups by exploiting a beautifully rich structure they collectively exhibit. Find out more on the next page...
About this article
Jeremy Hahn is Assistant Professor at the Mathematics Department of the Massachusetts Institute of Technology. Tomer Schlank is Visiting Associate Professor at the Mathematics Department of the Massachusetts Institute of Technology. |  Jeremy Hahn |  Tomer Schlank |
Marianne Freiberger is Editor of Plus. Together with Dan Aspel from the INI, she interviewed Hahn and Schlank in July 2023. You might also want to listen to this episode of the INI's Living Proof podcast featuring the interview.
This article was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.
The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.
