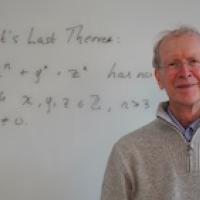
A very old problem turns 30!

"I think I'll stop here." This is how, on 23rd June 1993, Andrew Wiles ended his series of lectures at the Isaac Newton Institute (INI), our neighbour here at the Centre for Mathematical Sciences. The applause, so witnesses report, was thunderous. Wiles had just announced a proof that had eluded mathematicians for over 350 years: the proof of Fermat's Last Theorem.

Andrew Wiles, at the University of Oxford in 2023 (Image courtesy of the INI)

An infamous scribble

The theorem concerns equations of the form $$ x^n+y^n=z^n $$ where $n$ is a natural number. The question is whether there are triples of non-zero natural numbers $x,y,z$, that satisfy such an equation. For $n=2$ the answer is yes. There are in fact infinitely many such triples, known as Pythagorean triples, because the numbers involved also satisfy Pythagoras' theorem for right-angled triangles.

The 17th century mathematician Pierre de Fermat convinced himself that when the exponent $n$ is greater than 2, however, there are no integer solutions to the equation. In 1637 he wrote into the margin of his maths textbook that he had found a "marvellous proof" for this fact, which the margin was too narrow to contain. That tantalising scribble was to taunt mathematicians for a long time – Wiles was one of them.

"I first found out about Fermat's Last theorem from the cover of a book by E.T. Bell when I was about ten years old," says Wiles, who is now Regius Professor in Mathematics at the University of Oxford. "I was captured by the romantic history of [the problem], so I spent some of my teenage years and even [some time] in college trying to solve it. But then when I became a professional mathematician I realised that this was not something you should be working on because it probably wouldn't generate any results."

In the mid-1980s, however, work by the mathematicians Gerhard Frey, Jean-Pierre Serre and Ken Ribet provided a new way of attacking Fermat's Last Theorem. It showed that if you could prove another result, known as the modularity conjecture (also known as the Taniyama-Shimura-Weil conjecture) then you'd have automatically proved Fermat's Last Theorem too.

"I was sceptical when the first announcement came out, but when Ribet proved that connection I was completely hooked and I dropped everything and started working on Fermat straight away," says Wiles. Unusually for a mathematician, he decided to work on the problem alone and in secret, for a period of seven years. "Very few people want to work on a problem for that long. To really commit yourself to a problem takes a certain kind of personality. I did initially [talk about it] a tiny bit, but then I realised that it got so much unwanted attention when you said you were working on it, you wouldn't be left in peace. So I felt it was wiser to do it in private."

An electric atmosphere

Wiles finally proved the modularity conjecture, in a setting that was general enough to imply that Fermat's Last Theorem was also true. He announced his proof at the Isaac Newton Institute on June 23, 1993. The announcement came at the end of a series of three lectures and nobody really knew that this was what Wiles had had in store.

"Rumours started to get around," says Tom Körner from the University of Cambridge, who had the privilege of witnessing the lecture. "I do not know if people knew or just speculated, so I asked one of Andrew's students whether I would regret missing the lecture, and he said yes. The atmosphere was electric."

Andrew Wiles announcing his proof of Fermat's Last Theorem on 23 June 1993 (Image courtesy of the INI)

"At the end of [the lecture] Andrew wrote up the statement of Fermat's Last Theorem, and indicated that what he had done, he felt, had proved it. There was tremendous applause and then the experts got up and asked questions which indicated that, although details of the proof remained to be thoroughly checked, it was a very plausible way of attacking the problem. It was also a new way of attacking the problem, so that whether it succeeded or not, it had added a substantial amount to mathematics."

"On the one hand I was very excited to present [the result], but on the other there is always a tension the first time [you share the work]," says Wiles when recalling the announcement. "You have been thinking about this [for a long time], a lot of it on your own, so you [hope that you] haven't done anything stupid. I think people wanted to see the details, but they could see that this was a completely new approach and that it was going to prove something - whether it had all the details of the final claim remained to be seen."

The desire to see the details proved justified: it turned out the proof as it stood contained a hole, which it took Wiles, together with the mathematician Richard Taylor (who had been Wiles' former PhD student at Princeton), nearly a year to fix. But then finally, in 1994, the centuries old problem that was so tantalisingly inspired by a note scribbled in the margin of a book was finally solved.

The future of mathematics

You might think that, when an old problem is finally solved, a door closes on the area of mathematics involved. But this is rarely the case, as a solved problem usually opens up a range of unsolved ones. Wiles says that Fermat's Last Theorem has sparked two periods of intense progress in the past: one in the 19th century when the foundations for Wiles' areas of mathematics were laid in attempts to prove Fermat's Last Theorem, and one in the 1980s, which finally lead to the proof.

The proof itself, Wiles says, has helped to ring in a new era. "It opened another door, this time on problems of modularity. And these problems of modularity are themselves just one more door opening on this great perspective of what is called the Langlands programme — that's the future of mathematics."

It is difficult to explain the Langlands programme even to an expert, suffice to say that it consists of a web of far reaching conjectures made by Robert Langlands in the 1960s that draws extremely surprising connections between different fields of mathematics. Proving all these conjectures is seen by many as the single biggest project of modern mathematics.

Jack Thorne, at the International Congress of Mathematicians in 2018. You can learn more about his work in our interview.

The Langlands programme attracts some of the brightest minds in mathematics. Among them is Jack Thorne from the University of Cambridge. Thorne was six years old when Wiles announced the proof of Fermat's Last Theorem, and became interested in the result while doing his mathematics A levels.

"I found it quite exciting because doing A Level maths you learn how to do certain kinds of calculations, for example how to balance two balls on a rod and things like that," he says. "But this was the first time that I had seen a human story attached to a mathematical problem. Not just the story of one person, but people talking to each other over a period of centuries."

Despite his young age, Thorne is already a leading expert in his field. He has won a number of prizes, including the prestigious New Horizons in Mathematics Prize, and became the youngest living fellow of the Royal Society when he was elected in 2020. Thorne works on the Langlands programme, in particular on the connection it provides between number theory on the one hand and an area of maths that comes from generalisations of objects called modular forms on the other. "They are two worlds [for] which, a priori, it is not clear they should be connected, but [which] talk to each other in ways that are very mysterious and very striking," he explains. "It's really like there's a hidden telephone line."

The Langlands programme provides new tools for attacking problems in number theory. Thorne has used these tools to consider equations similar to the one of Fermat, but slightly more general: rather than requiring all the coefficients in the equation to be integers, you can ask yourself what happens if the coefficients come from larger number fields, for example fields containing more awkward irrational numbers such as the square root of 2. For some such classes of equations the theory generalised beautifully, says Thorne, but much work is still needed to push the field further. Wiles agrees that extending our theory of arithmetic to encompass more general number fields, using the tools provided by the Langlands programme, is one of the most important challenges of the future.

So while Wiles' proof settled a problem that is so easy to state that even a high school student can understand it, it has opened the door on a deep new area of mathematics which will see exciting developments in the next decade or so, in which mathematicians like Thorne are likely to play a leading role.

A key moment

That moment 30 years ago was clearly a turning point in Wiles' career. He is one of the few mathematicians who is well-known outside of mathematics, and was recognised with a knighthood in 2000. Within mathematics he has received a wealth of honours and awards, including the prestigious Abel Prize in 2016.

The announcement of the proof was also a key moment in the history of the INI. "Still in its first year of operation, the Institute became suddenly part of world frontpage news, something that is rarely achieved in mathematics," says Ulrike Tillmann, Director of the INI. "We are ever so grateful to Sir Andrew Wiles for choosing the Institute to announce his extraordinary breakthrough."

It's been such a pleasure to revisit this moment with all of these mathematicians, to hear the human story, as well as the mathematical one. Wiles told us, back in 2016, about some of the personal qualities a mathematician has to have – they have to be creative, and they have to be able to enjoy being stuck. And perseverance again appeared as a key thread in the story when we spoke to him for this article. Our final question was whether he would have kept on working on Fermat's Last Theorem even if he hadn't found a solution back in the early 90s. His answer was characteristic of his approach to mathematics: "I am not a person who gives up on a problem."

About this article

Marianne Freiberger and Rachel Thomas, Editors of Plus, interviewed Tom Körner, Jack Thorne and Andrew Wiles in May and June 2023. They'd like to thank Dan Aspel, from the Isaac Newton Institute, for his help with these interviews.

This content was produced as part of our collaboration with the Isaac Newton Institute for Mathematical Sciences (INI) – you can find all the content from the collaboration here.

The INI is an international research centre and our neighbour here on the University of Cambridge's maths campus. It attracts leading mathematical scientists from all over the world, and is open to all. Visit www.newton.ac.uk to find out more.