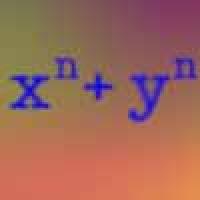
Another proof for Fermat's last theorem

06/05/2005

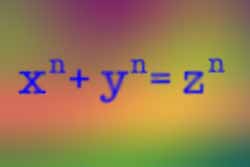
Fermat's last theorem says that this equation can't be satisfied for n greater than 2

Chandrashekhar Khare, a mathematician from the University of Utah, has announced that he has proved what is known to experts as the "level-one Serre conjecture". This conjecture was posed in 1972 by the Fields medallist Jean-Pierre Serre, and belongs to the field of Arithmetic Algebraic Geometry. At this point we should of course say what the conjecture states, and explain its importance in the real world. This, however, is easier said than done, as those of us who are not experts would have to spend several months studying seriously advanced mathematics, just in order to understand the statement.

Luckily though, the conjecture belongs in a wider context - which we can attempt to explain - and has a famous relative: Fermat's last theorem. Serre's conjecture is in a sense a parent of Fermat's last theorem: mathematicians have known for some time that if the first is true then so is the second. In fact, it is a certain part of the conjecture which implies Fermat's last theorem, and this part was proved by Khare and his collaborator J.P. Wintenberger, and independently by the mathematician Dieulefait.

Fermat's last theorem states that if $n$ is a whole number strictly bigger than 2, then you can never find three whole numbers $x$ , $y$ and $z$ such that $x^ n+y^ n=z^ n$ .

Andrew Wiles, the man who tamed Fermat.

This seems simple and has tempted many people to retire to a corner with paper and pencil and try to prove it. It is, however, devilishly hard and it wasn't until 1995 that Andrew Wiles, with the help of Richard Taylor, famously cracked the problem. Although the theorem is primarily a theorem about numbers, thus naturally belonging to the realm of number theory, to prove it Wiles had to wheel up heavy machinery from two other areas of maths: algebra and geometry.

The fact that algebra, geometry and number theory are related can be seen using very simple maths: circles and straight lines, which are geometric objects, can be expressed by algebraic equations. If or where a circle meets a straight line can be determined by solving a set of algebraic equations, which is of course also an exercise in number theory.

But it isn't just that algebra and geometry were used to solve Fermat's last theorem. In fact it, as well as the conjecture by Serre, are ingredients of a wider program to unify various areas of mathematics, known as Langlands philosophy. The idea behind such unifying theories is that it should be possible to directly translate every concept in a given area of maths into all the other areas of maths. Every object and concept in algebra, for example, should have a counterpart in geometry, and vice versa, and the relationship between the objects should be the same in both areas. For example, a circle and a line both have algebraic equations, and the circle and the line meeting in one, two or no points corresponds to a certain equation having one, two or no solutions.

The Langlands philosophy was conceived by the mathematician Robert Langland in the 1960's and consists of a set of conjectures concerning the intimate relationship between number theory, geometry and algebra. What both Wiles and Khare have done is to prove bits of these conjectures, which in turn imply Fermat's last theorem.

Khare's result came as a bit of a surprise, as no one was expected to solve this problem so soon. It is currently undergoing the meticulous scrutiny of fellow mathematicians, who will hopefully declare it fit for publication. Serre himself is said to be "happy and excited".

Another proof for Fermat's last theorem

Further Reading