
Arithmetic, bones and counting
| "It is unworthy of excellent men to lose hours like slaves in the labour of calculation, which could be safely relegated to anyone else if machines were used." Gottfried Wilhelm von Leibniz, 1671. |
Position is key
The decimal system, with which we write numbers, is one of the most important contemporary pieces of scientific technology. You may not have thought of it as such, but really it is. The decimal system of writing a number, such as two hundred and fifty-three, in the compact form 253, is an exquisite technological innovation. Indeed, as the eighteenth century mathematician Pierre-Simon Laplace comments:
| "The idea of expressing all quantities by nine figures whereby is imparted to them both an absolute value and one by position is so simple that this very simplicity is the very reason for our not being sufficiently aware how much admiration it deserves." |
The exact origins of the system of number bases is hidden. Certainly the ancient Babylonians used a place value system with base sixty. We also know that from 2000 BCE peoples in the Indian subcontinent had number words for 1 to 9, 10, 100 and further powers of 10, up to 1010. They definitely seemed to use a base ten system, although this may have been developed much earlier. The critical innovation, developed by the ancient Indians and lacked by the Babylonians, is the concept of a zero as a place holder. This knowledge was developed by scholars in the Middle East who around the 7th century BCE translated many mathematical books from the Greeks and Hindus. They later travelled to Western Europe, probably through trade with Italy. In particular, it was almost certainly through the needs of merchants that the place value system was introduced into Europe. Leonardo of Pisa, better known as Fibonacci, wrote his book Liber Abaci in 1202, and in it used the place value system.
However, people only started regularly writing down numbers in the way we do now after about 1550. There are a number of possible reasons. People were suspicious of an imported "infidel" system. Negative numbers caused much confusion and people referred to them as "fictional" or "absurd" amounts and often used them in a clumsy way. The purpose and nature of the symbol 0 caused even more difficult conceptual problems, and in practice accounts were easy to falsify.

John Napier, 1550 - 1617.
We now take the decimal system for granted. We also take for granted the machines that, as Leibniz predicted, perform most of our calculations. In this article, however, we step back to a time long before electronic computers first appeared. We'll explore two ingenious mechanical devices that exploit the advantages of the positional system to perform otherwise long and tedious calculations. The devices were developed by John Napier, who is better known for inventing the logarithm, and appeared in his book Rabdologiæ, sev nvmerationis per virgulas libri duo, published in 1617 shortly after his death.
Rabdology did in fact contain three mechanical aids to calculations. In this article we'll focus on two of them: a set of counting rods commonly known as Napier's Bones, and a counting board using binary arithmetic, referred to by Napier as location arithmetic. Napier's third device, the promptuarium, is just as ingenious. It consists of strips of paper on which are written multiplication tables in a cunning configuration. The calculation is revealed by placing these strips below others with holes cut in, so that the answer can simply be read off the device. We don't have the space to explore the promptuarium here, but we hope that our two examples suffice to convince you of Napier's ingenuity and the great versatility of the place value system.
Napier's bones

Figure 1: Faces of Napier's bones. Each strip represents a multiplication table of one of the digits from 0 to 9. Tens are written above the diagonal and units below.
We shall explain how to perform multiplication using the example given by Napier, that is to say "let it be required to multiply the year of the Lord 1615 by 365". There are two ways to perform this calculation. First we shall take the rods headed by 3, 6 and 5 and place them in this order, side by side. This arrangement is shown in figure 2 and effectively gives a 365 times table. The top row is 365 × 1, the second row 365 × 2, etc.
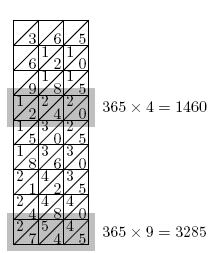
Figure 2: Using Napier's Bones to calculate multiples of 365.
Using normal long multiplication we have that
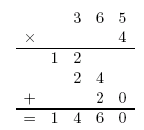
This calculation can be done simply by inspection, since the diagonal lines allow us to sort out the necessary carries simply by looking. Sometimes carries will roll over into columns further to the left. For example, when calculating 365 × 9, the 5 + 7 in the hundreds columns forces an extra carry into the thousands, giving the result 3285, but this is simple arithmetic and in reality causes no confusion.
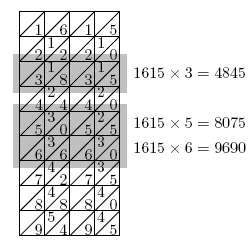
Figure 3: The faces of the bones give the multiplication table of 1615.
What Napier's Bones do is to immediately assemble multiplication tables from the tables for the digits 0 through to 9. This is possible because of the positional features of the place value system. The tables can themselves then be assembled into more complex calculations, such as Napier's 1615 × 365, illustrated in figure 3. To calculate 1615 × 365 Napier recommends using the rods with the number containing the larger number of digits, in this case 1615, so that here you need two copies of the 1 rod. Then write the other number on a page and underline it. Next read off the product of, in our case 1615, and each digit of 365. These are written down one above each other but shifted so that the least significant digit of each product lies directly below the digit itself. For example, the digit 5 in 4845 should be written directly below the 3. The full calculation is:
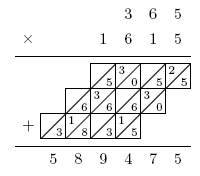
Making a set of rods
In performing calculations, we have tacitly assumed that we have available an unlimited number of paper strips marked out with the multiplication tables of the individual digits. In fact, Napier used square rods with each face marked by a strip. But this leaves us with a problem. In a calculation, such as 1615 × 365, we might need to use two of the faces on one particular rod at the same time. Equally we don't want to make too many rods, which would waste effort, and be bulky to transport. Let us assume that we want sufficient rods to calculate products of numbers with four digits, that is using numbers up to 10,000 = 104. Clearly we will need four copies of each digit's table, giving 40 strips. Therefore, ten square rods is the absolute minimum needed. In fact, ten rods properly marked out are sufficient for calculations with any numbers less than 11,111.
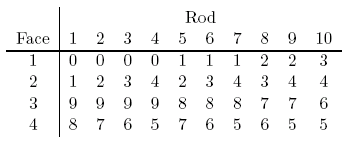
Table 1: The configuration of faces on Napier's Bones.
Napier did use ten rods, whose faces he marked out in a cunning and systematic way. Each face of the rod contained the complete strip given by one of the numbers between 0 and 9. Napier ensured that the sum of the 1st and 3rd faces was 9, and the sum of the 2nd and 4th faces was also 9. In this way he could concentrate on only the first and second faces, and fill in the others with complementary numbers. To understand Napier's systematic procedure, have a look at the first two rows of table 1. The first four rods have 0 on the first face. The second three rods have 1 on the first face and so on. These are paired with other numbers for the second face in such a way that every combination of two different numbers from 0, 1, 2, 3 and 4 are chosen. Each digit is shown exactly four times. As Napier says "The arrangement given above offers the greatest flexibility. Although other arrangements are possible, none is superior to this, and none can express more number with so few rods."
Sets of rods can be combined, so 20 rods are sufficient for numbers up to 108, 30 rods for numbers up to 1012, and so on. Actually, Napier wrote faces 3 and 4 on the rods upside down. A complete set of ten rods is shown in figure 4. (If you'd like to make your own rods, download the figure in PDF format, enlarge and print it, and then cut it out and glue it onto rods.)

Figure 4: A complete set of Napier's Bones.
Napier's location arithmetic
The next device of Napier's that we consider is his counting board, which appears in book III of Rabdology and is described as location arithmetic. This relies on base two, or binary, representations of numbers, and for its time was hugely innovative. Recall that in binary only the digits 0 and 1 are available and the place values of each column are powers of two. That is to say
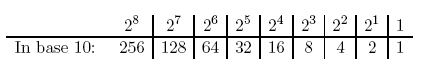
So counting in binary begins with the following pattern:
One effective method to write a particular number in binary, such as three hundred and sixty-five, is to use a greedy algorithm — "greedy" because we begin with the largest power of two less or equal to our number. Clearly 28 = 256 fits the bill in this case, so we subtract this to get (in base 10 notation):
Now we repeat this process with 109 taking the largest power of two, which this time is 26 = 64, and getting
This continues with 45 and repeats until there is nothing left. The important point to remember is to always remove the highest power of two possible. In the end we come up with the binary representation 101101101 for three hundred and sixty-five. Napier represented this number using counters on a board. The resulting representation of 365 is
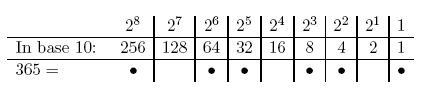
In fact, Napier proposed using a two-dimensional board with counters, and a standard draughts board works very well indeed for calculations of numbers up to 28 - 1 = 255.
In his scheme the value of a counter on the board is determined by its position:
Respecting the way we usually write numbers, we shall start counting our columns from right to left, starting with the 0th column. This is illustrated in figure 5. A number of counters have been placed on this board, labelled by the value they represent in their current position. So, looking in the forth column from the right, we notice that moving up or left one position doubles the value of the counter. Hence, we could take two counters from one square and replace them with one counter in a square one to the left, without altering the total on the board. Notice the diagonals from bottom left to top right all have the same value. This is illustrated using the counters with value 8.
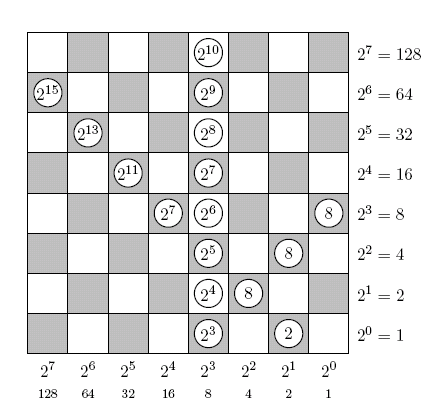
Figure 5: Napier's location arithmetic.
The most important observation connected with Napier's counting board is this: we can slide counters diagonally up and right, or down and left without altering their value. This allows us to calculate the product of two numbers by sliding counters around, much like draughts moves. We shall illustrate the process by calculating the product 5 × 11.
To begin the process, we use the columns to represent one number in binary — say the 11 — and the rows to represent the other. Since eleven has the binary representation 1011, and five has the binary representation 101, we end up using the following marked rows and columns.
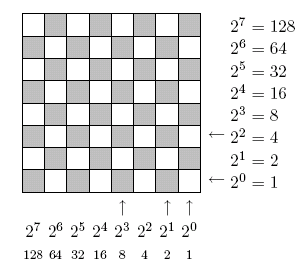
Next, we identify all the squares which have both the row and column marked. Add counters onto the board, in every such square. This corresponds to performing all the various cross multiplications when using binary long multiplication. Put another way, there is one counter for each multiplication when we expand out the two brackets.
Next, slide all the counters diagonally down and left, until they all occupy the bottom row. Note, this does not change any of the values represented by the counters. At this stage, it is perfectly acceptable (and may well be necessary) to have more than one counter per square.
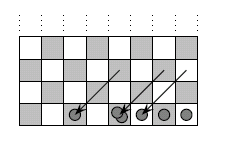
Working from right to left along the bottom row, in any column that contains more than one counter, remove two and place one in the column to the left. Again, this process does not alter the total value of counters on the board. Effectively this sorts out the arithmetical carry operations.
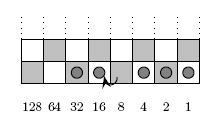
If necessary, translate the product back to decimal. Of course, you might be happy with the board set up as it is, if you intend to continue with further calculations. In our case we end up with the total 32 + 16 + 4 + 2 + 1 = 55, as expected.
Other calculations are, of course, possible with a counting board of this type, including addition and subtraction, with counter moves sorting out carry and borrow operations. Napier also gives rules for division and square root extraction.
There are only practical limits on the size of grid, since there is no need to restrict to the 8 × 8 chess board. Indeed, extending the board down and to the right could add room for fractional calculations using negative powers of two.
The need for people to perform large numbers of repetitive calculations has been removed quickly and accurately by modern electronic computers and pocket calculators. However, it is still important to understand how the arithmetic operations work. The inventions of Napier, which we have examined here, are interesting and practical variations on traditional paper and pencil methods. You should try them out for yourself, as making a set of Napier's Bones is enjoyable and interesting.
About the author

Chris Sangwin is a member of staff in the School of Mathematics at the University of Birmingham. He has written the popular mathematics books Mathematics Galore!, with Chris Budd, and How round is your circle? with John Bryant.
Comments
Al Martin <nitrama@gmail.com>
Hello, the diagram for making your own bones has an error. The first bone should be 5-6-4-3, not 5-7-4-3. Opposite sides should add to 9, and there should be 4 columns of each number in the complete set.
Mr. Robert Ward
Your comment on Napier's board, 'looking at the forth column from the right. Should of course be the fourth column. Nice article though. Thank you.
Walt R
In Figure 5, the values of the token in the leftmost three columns are off by a factor of 4 - it looks like the up-left increment of two in the exponent was carried out one too many times.