
The butterfly flap felt across the world
Edward Lorenz, American mathematician and meteorologist, died in his Cambridge Massachusetts home on April 16 aged 90. Lorenz was known as the father of chaos theory and discovered the Lorenz attractor that often occurs in chaotic systems.
Lorenz is perhaps best known for coining the term butterfly effect. Whilst a professor at the Massachusetts Institute of Technology, Lorenz developed the concept that tiny effects in one part of a system can lead to big changes in another part. The term butterfly effect first appeared in his 1972 paper Predictability: Does the flap of a butterfly's wings in Brazil set off a tornado in Texas?.
Lorenz started to develop his theories of chaos as a meteorologist running computer simulations of basic weather patterns. The simulations were governed by a set of differential equations, and each simulation had its own initial values. One day Lorenz ran the same simulation twice and to his surprise found that the two rounds resulted in completely different weather predictions. He soon found out why: the initial values of the second round had been rounded off by a seemingly insignificant amount — the computer stored numbers to an accuracy of six decimal places, while the results were printed to three decimal places. When typing in the new conditions, Lorenz entered the rounded-off numbers (0.506 rather than 0.506127, a difference of less than 0.1%). This tiny difference of starting values caused the equations to spit out a completely different set of answers. To mathematicians this effect is known as sensitive dependence on initial conditions and it is one of the hallmarks of mathematical chaos. It means that even though your equations can predict the long-term behaviour of your system in theory, in practice they will never be able to do so, since an infinite degree of accuracy would be required to differentiate between initial values that lead to completely different outcomes.
In 1963, Lorenz introduced the concept of what became known as the Lorenz attractor in his seminal paper Deterministic nonperiodic flow in the Journal of the Atmospheric Sciences. The Lorenz attractor, which when plotted ironically looks like a butterfly, arises from a set of three equations that show how a dynamical system can produce complex, non-repeating patterns. The Lorenz attractor describes the conditions that make the system behave chaotically.
The equations that govern the Lorenz attractor are \ $$ \frac{dx}{dt} = \sigma (y - x); \frac{dy}{dt} = x (\rho - z) - y; \frac{dz}{dt} = xy - \beta z; $$
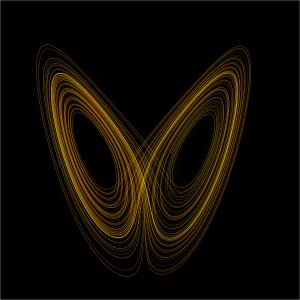
Lorenz attractor with r = 28, σ = 10, β = 8/3
Initially, Lorenz used these equations to model convection in the upper atmosphere. Imagine a simple system in which you have a box full of homogeneous gas. Now imagine that we heat the box. Warm air rises and cool air sinks, so initially the gases nearest to the walls (the heat source), start to rise. This creates a cylindrical flow, with air rising on one side and sinking on the other. This pattern may seem predictable, but at some later time, chaotic motion evolves and the gas flow reverses direction and changes speed, seemingly randomly.
A two-dimensional physical demonstration of this is the waterwheel. Imagine a waterwheel in which all the buckets have identical holes in their bottoms. If we begin a flow of water into the top bucket, at low speeds the water will immediately trickle out through the hole and not turn the wheel. If we increase the flow however, the buckets will fill more quickly than they can empty, and so the waterwheel will revolve. Heavy buckets drip as they descend becoming lighter. As the waterwheel turns, light buckets rise on the other side. These buckets then get filled and become heavy again and the waterwheel continues to turn — the system is in a steady state. However, if we increase the flow of water even more, the waterwheel will revolve in one direction as before, but then may suddenly revolve in the other direction — the motion has become chaotic. This is because with a high flow of water, the wheel initially spins very quickly. By the time the heavy buckets of water have revolved to the opposite side of the wheel, not much water has flowed out from them and they remain relatively heavy. If the wheel was spinning so quickly that new buckets being filled spend too little time under the flowing water, then the side of the wheel that was previously heaviest is now the lightest, and the rotation reverses. A nice demonstration of this can be found on Lorenzian Waterwheel.
On Lorenz being awarded the 1991 Kyoto Prize, the judging committee stated that his discovery of "deterministic chaos" brought about "one of the most dramatic changes in mankind's view of nature since Sir Isaac Newton." With no Nobel prize for meteorology or mathematics, this was high praise indeed. He also won the 1983 $50,000 Crafoord Prize which recognizes leaders in scientific fields not eligible for a Nobel prize.
Further reading
See the following Plus articles for more information on chaos and the Lorenz attractor: