If you are prone to forgetting your passwords, you're not alone. To make sure we remember all our passwords, many of us take measures that defeat the purpose. These include, as studies have shown, using the same password for everything, with things like "password1" or "abc123" particular favourites, or writing them down on post-it notes and sticking them to our computer. But such sloppiness makes easy work for evil agents out to steal our data and identities. And with no small effect. Recent studies have revealed that identity theft affects nearly 10 million people in the US each year and in 2006 alone cost the US economy more than $55 billion.

But now physicists from the US and Germany have devised a safer way of using passwords that takes account of the human need for memorability. It exploits mathematical chaos and our ability to recognise images much better than computers can.

Conventional methods of protecting personal data, for example your bank account details, rely on encryption algorithms. These shuffle and substitute the symbols in the message that's to be encoded according to a specific recipe. While the recipes themselves are publicly available, the Advanced Encryption Standard (AES) used by the US government is an example, parts of them depend on a cryptographic key, for example a user-chosen password, and only those in posession of the key can run the algorithm backwards to decrypt the message.

If passwords were just long and random strings of characters, then brute-force attacks, trying out all possible passwords, would be unfeasible. But with a severely limited password pool, resulting from people being sloppy in their password choice, such attacks become possible. Computers can be programmed to try out each one of the possible passwords to obtain a text that may be the true message. They can then search this text for patterns, correlations and other tell-tale signs to see if it represents meaningful information. If it does, then the password has been cracked.

The new method, proposed by T.V. Laptyeva and S. Flach from the Max-Planck-Institute for the Physics of Complex Systems in Germany and K. Kladko from Axioma Research in the US, also uses standard encryption algorithms, like AES, but it works some magic with the password. It uses a long password consisting of two parts. One part is an easily memorable short password and the other is longer and known as the strong key. The confidential text is encrypted using a standard algorithm like AES and the combination of short password and strong key as the password.

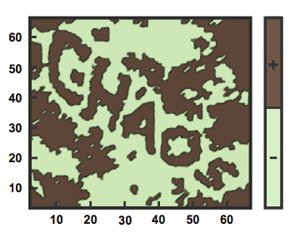
The strong key — in this example the word "chaos" — is embedded in an image.

The strong key doesn't have to be memorised by the user. Instead, the strong key is embedded in an image in a similar way as for the familiar CAPTCHA test, which shows the user a distorted image of a word which computers used to find difficult to identify (though good image recognition software is more successful).

But here's the trick: the image can also be interpreted as a snapshot in time of a dynamical system — a system that evolves over time according to a set of mathematical equations. The state of the system at each individual time step can be described using numbers and represented by an image.

The particular dynamical system used in this case comes from physics, where it is used to model the behaviour of ferroelectric materials, such as barium titanate. These are akin to magnetic materials, but rather than responding to magnetic fields, they respond to electric fields, becoming electrically polarised when an electric field is applied.

Ferroelectric materials lose their ferrorelectric property at a certain temperature. Such a sudden change in a material's porperties is called a phase transition. Typically a system undergoing a phase transition moves from an ordered state — electric polarisation in the case of ferroelectric materials — to a disordered state. The dynamical system the researchers chose for their encryption method is a simple model of the behaviour of ferroelectric materials close to the phase transition. One of the properties the system exhibits near this order-disorder transition point is chaos: parameters describing the system fluctuate wildly and the system is so sensitive to small changes that it is impossible to predict exactly what state it will be in after a number of time steps.

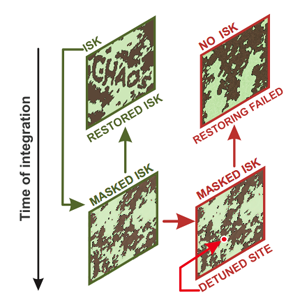
The image containing the strong key (called the ISK) is evolved in time (downward direction). Even the smallest change in the resulting image will cause you to miss the original when you go back in time.

Now suppose you have arrested this dynamical system at a particular moment in time, say at time $t_0$. The encryption method works by embedding the strong key in the corresponding image using something akin to the CAPTCHA method. The system is then allowed to evolve for a certain number of time steps, until it reaches time $t_n$. The state of the system at time $t_n$ will have similar overall features for whatever initial state $t_0$ we start with, but due to the chaotic dynamics the precise nature of these features is impossible to predict and they appear random. The numerical information which encodes the state of the system at time $t_n$ can therefore be split into two parts. One part describes the regular features of the system — this can be stored in plain text. The other describes the random-looking detail and is encoded using the short password.

Now imagine that you're the legitimate user in possesion of the correct short password. You enter this short password, which decrypts the random-looking part of the information. This is then combined with the information that encodes the regularities of the dynamical system, to give you all the information about the system at time $t_n$. The system is now evolved backwards in time until it gets back to time $t_0$. In theory, such a backward evolution does not always get you back to the exact state you started from: because the system is chaotic, the smallest inaccuracy in your information (coming for example from rounding off numbers) can amplify as you move backwards in time and cause you to miss the original image. But by making sure you don't use too many time steps (i.e. that the number $n$ isn't too large) you can guarantee that you end up with something nearly identical to the original image. Then, instead of having to remember it, you can just read the strong key off that image. It is now combined with the short password to give you the overall password which decrypts the original data.

But what if you're a hostile attacker systematically trying out a large number of short passwords? Suppose that you have access to the plain-text information describing the regular features of the dynamical system at time $t_n$ and to the encrypted data representing the random-looking part. First you use a particular short password guess to get a candidate decryption of the random-looking part. Usually the candidate decryption would be searched for patterns and correlations which indicate if it's the true text. But in this case the true text itself looks random, so any such search is futile. You just have to plough on: you evolve the system backwards until time $t_0,$ hoping that the resulting image contains the correct strong key.

But, because of the chaos in the system, the slightest error in your image at time $t_n$ means that you miss the correct image altogether. More importantly, it is nearly impossible for a computer to decide whether or not it is looking at the correct image in a reasonable amount of time. This is because all images produced by the dynamical system have similar overall structures, so there are no specific patterns that will tell the computer it is looking at the correct image. And while image recognition software may be able to see if the image contains a word, it needs a lot of time to do this and therefore a rather small pool of possible short passwords already produces an unfeasibly long hacking time.

The researchers believe that the new method has significant potential. "Our method can be readily and straightforwardly implemented on a wide variety of existing computer systems and devices and, to our view, provides a significant step forward in protection of confidential data," they say in their paper which has yet to be published in a peer-reviewed journal. There is also room for further research, for example checking whether other dynamical systems provide a better basis for the method. But whether or not the new method will be used as it is or developed further, it's nice to know that mathematical chaos will enable our brains to continue to wander freely.

Further reading

You can find out more about commonly used encryption algorithms in the article Safety in numbers and about cryptography in general on Plus.